迄今为止见到过的一个超级妙的关于%的计算!!!!!!!

Posted 2021-06-26 捕获一只小肚皮

前言

博主今天翻阅以前刷过的一些题,然后突发奇想,有没有人有不一样的解法,好家伙,还真给我逮到了.于是就看了看,实在被那个大佬的解法给震惊,因此记录下这篇文章.此外,博主关于这个公式的推导完全是基于自己主观来的,若评论区有大佬觉得不够严谨,欢迎斧正.

---

文章目录

• 前言
• 题目
• • • 普通方法
    • 重头戏----优秀方法

题目

幻方是一种很神奇的 NxN 矩阵：它由数字 1,2,3.......N×N构成，且每行、每列及两条对角线上的数字之和都相同

其中,输入的N一定是奇数

比如 N=5时候:

比如N=7时候:

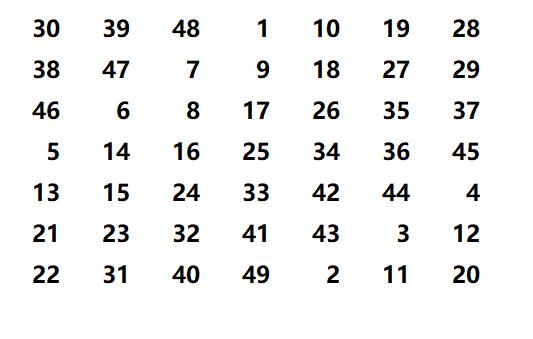
那么如果我们要用程序实现这个怎么搞???我们可以看看规律

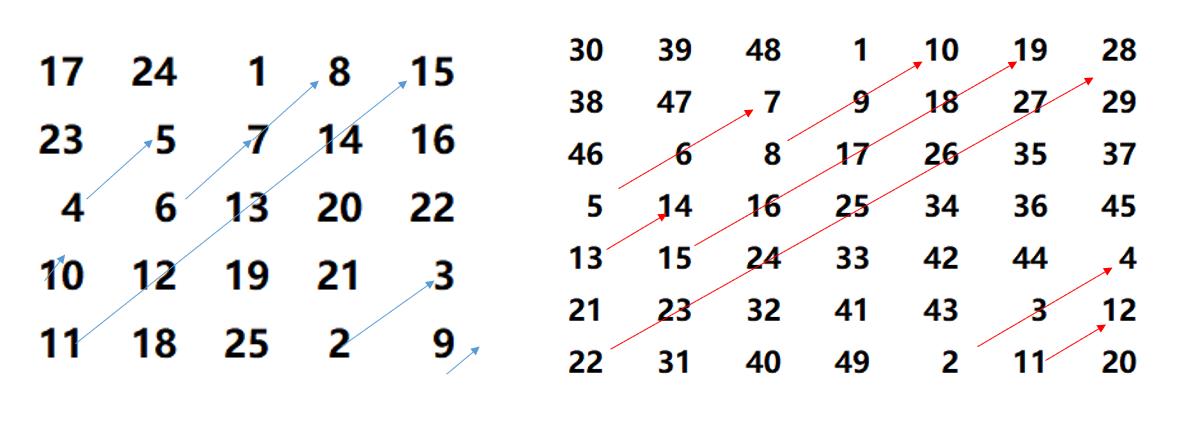
规律就是1的下标一定是在第一行的中间列-----------随着从1到nxn的增加,每个数字都向右上走,如果右上角有数字就向下走一个.且不能超出边界.

标准叙述:

首先将 1 写在第一行的中间。

之后，按如下方式从小到大依次填写每个数 K(K=2,3,⋯,N×N) ：

若 (K-1) 在第一行但不在最后一列，则将 K 填在最后一行， (K−1) 所在列的右一列；
若 (K-1) 在最后一列但不在第一行，则将 K 填在第一列， (K−1) 所在行的上一行；
若 (K−1) 在第一行最后一列，则将 K 填在 (K−1) 的正下方；
若 (K−1) 既不在第一行，也不在最后一列，如果 (K−1) 的右上方还未填数，则将 K 填在 (K-1) 的右上方，否则将 K 填在 (K−1) 的正下方。
现给定 N ，请按上述方法构造 N×N 的幻方。

普通方法

-------按照规律进行模拟,在这里就不再赘述,直接贴代码,因为重头戏是 后面的%

#include <stdio.h>

int n,a[10010][10010],x=1,y,cnt=2;//cnt赋值为2，因为从2开始填数

int main()
{
	scanf("%d",&n);//输入不解释
	y=(n+1)/2;//将x,y的值（k-1)坐标赋值为1,(n+1)/2;
	a[x][y]=1;//将第一行最中间的数赋值为1.
	int now=n*n;
	for(int i=2;i<=now;++i)
	{
	    if(x==1&&y!=n)//模拟第一种情况
	    {
	    	a[n][y+1]=cnt;
	    	x=n;
	    	y+=1;
	    	cnt++;
		}
		else if(x!=1&&y==n)//注意有else模拟第二种情况
		{
			a[x-1][1]=cnt;
			x-=1;
			y=1;
			cnt++;
		}
		else if(x==1&&y==n)//模拟第三种情况
		{
			a[x+1][y]=cnt;
			x+=1;
			cnt++;
		}
		else //第四种情况
		{
			if(a[x-1][y+1]==0)//如果k-1右上方还未填数
			{
				a[x-1][y+1]=cnt;
				x-=1;
				y+=1;
				cnt++;
			}
			else//反之~
			{
				a[x+1][y]=cnt;
				x+=1;
				cnt++;
			}
		}
	}
	for(int i=1;i<=n;++i)//完美输出
	{
		for(int e=1;e<=n;++e)
		printf("%d ",a[i][e]);
		printf("\\n");
	}
    return 0;//好习惯；
}

重头戏----优秀方法

在开始之前要知道个性质(其实大家都知道,我只是再说说以便后面印象深刻)

x % n的结果是:

• 当0 ≤ x < n时候,值是x.
• 当x = n时候,值是0.

开始:

我们根据规律可以更加仔细的看出,假设i是行,j是列.

那么j的变化规律一直是什么??? 1,2,3......n,1,2,3......n,1,2,3......,对,没错,j一直在增加,然后到n以后,又从1开始.

那么i的变化规律一直是什么??? n,n-1,n-2...3,2,1,n,n-1,n-2...3,2,1,n,n-1,n-2...,对,没错,i一直在减少,到1后,又从n开始

先看列的情况:

我们想要实现列一直增加怎么写???

• 首先肯定是这样j = j + 1 ,

但是这样让j循环下去.可以吗? 不可以.因为j会越界.

那怎么办?

• 我们看看越界时候j是啥值?
  • 当j=n时候,下次就会变为n+1了,就会越界!! 我们的目的确是让j从n变为1

所以我们就把 边界n给抵消掉,怎么抵消??? 那就是%n .

所以最后变为 y = y % n + 1

按照最开始博主写的%的两条性质推理可得:

• 当y的取值是[1,n-1]时候,等价 y = y+1;

• 当y的取值是n时候,下次y就会变为1.

注意: 有的人可能会想,这样也可以哎 y = (y+1) % n,注意哦~~~~~,这样写y的值永远不会到达边界哦!!!

再看行的情况:

我们就发现了个问题,好像从小到大,我们利用求余数进行从头循环,都是数字逐渐增大,现在要求从大开始逐渐变小,就有点难写了.

但是不要慌张哦~,我们一步一步的推一下逻辑

• 首先,我们肯定要让i不断减下去.所以i = i - 1.----------------------------------------------------------①

但是这样行吗? 不行,因为最后i会继续减少,变为0,但是i的范围只能是[1,n],所以越界了

那么我们能不能借一借列的思路,求一下模呢? 试一试

• i = ( i - 1) % n--------------------------------------------------------------------------------------------------②

但是这样好像还是没有解决掉哎. 因为按照博主最开始写的%的两条性质 ,①与②是等价的.但是我们肯定能猜到,这个倒着循环的数,一定与%有关系.

嗯…我们再借鉴一下列的思路,上面是针对边界情况分析,我们也试试.

边界情况是啥? i = 1时候. 我们的目的是让i-1 = 0时候,下一次i = n. 怎么办??怎么办??快想想???

咦?? 我们好像可以给i-1加个 n,(即这样i = (i-1 + n)%n),这样i下次就可以变为n了,但是好像这样子i-1等于0时候,就剩为n%n了.嗯???n%n好像等于0哎! 不对不对.

怎么办??? 那我们就退而求其次吧~~~~~,加一个n-1吧,这样最后i-1=0时候就变为(n-1)%n了,但是这样的值是 n-1哎,没事了!!!

我们可以加个1.

• 所以最终变为(i-1 + n-1)%n + 1,即(i - 2 + n) % n + 1-----------------------------------------③

大家试试,比如n=7时候,i从7开始下降,看看i的值是不是从7到1,然后又从7到1?,答案是肯定的.

所以这个题目的代码思路是:

先把1的位置写好,然后判断下一个位置是否有数字了,如果没有,就填进去,如果有,就列不变,填在下一个位置的垂直向下处.

#include<stdio.h>

int n,a[40][40] = {0},x,y;

int main()
{
    //开始输入1和n
	scanf("%d",&n);
    
	i=1,j=(n+1)/2;
    
	for(int m=1;m<=n*n;m++)
    {
		a[i][j]=i;
		if(a[(i-2+n)%n+1][j%n+1] == 0) //判断下一个位置是否空
            i=(i-2+n)%n+1,j=j%n+1;
		else 
            i= i%n+1; //如果下一个数字不为空了,就往下移动一下.
	}
    
	for(int i=1;i<=n;i++)
    {
		for(int j=1;j<=n;j++)
        {
			printf("%d ",a[i][j]);
		}
		printf("\\n");
	}
}