生成对抗网络（GAN）详细介绍及数字手写体生成应用仿真（附代码）

Posted 2021-06-26 康x呀

生成对抗网络（GAN）详细介绍及生成数字手写体仿真（附代码）

• 生成对抗网络简介
• • 深度学习基础介绍
  • • 损失函数与梯度下降
    • 反向传播算法推导
    • 批量标准化介绍
    • Dropout介绍
  • GAN原始论文理解
  • • 生成对抗网络基本介绍
    • 生成对抗网络理论推导
    • • 数据生成
      • 生成器——制造数据
      • 计算差异
      • 判别器——学习数据差异性
      • 最大化差异推导
      • 优化过程
    • GAN原始论文算法步骤详述
    • • 判别器训练算法
      • 生成器训练算法
    • GAN存在的问题
    • • 可解释性非常差
      • 训练不稳定
      • 优化震荡现象
      • 生成器容易产生模式崩溃（Mode collapse）
• 数字手写体生成应用
• • 数字图像生成介绍
  • 生成器网络结构初始化代码
  • 判别器网络结构初始化代码
• 仿真结果
• 其他

生成对抗网络简介

深度学习基础介绍

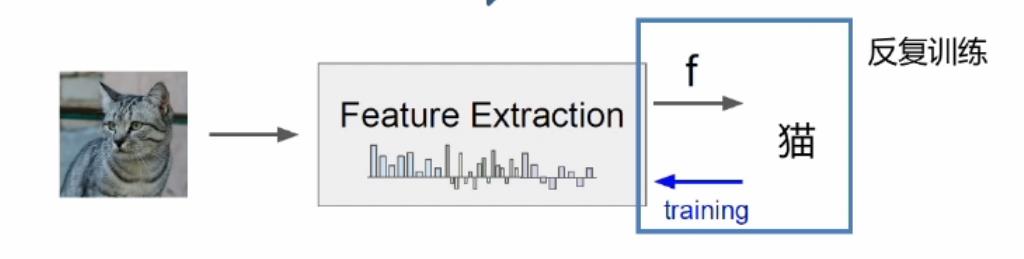
以上图举例子，假如要识别这只猫，在这里猫是一张图片，里面全是一些像素点，因此我们首先要对它进行一些特征提取，提取出猫的眼睛、鼻子、耳朵、花纹等特征。然后对这些提取出的这些特征进行学习，然后去识别这到底是不是一只猫，通过学习不停反复进行训练提取后的特征。然而会导致信息严重的丢失等问题。

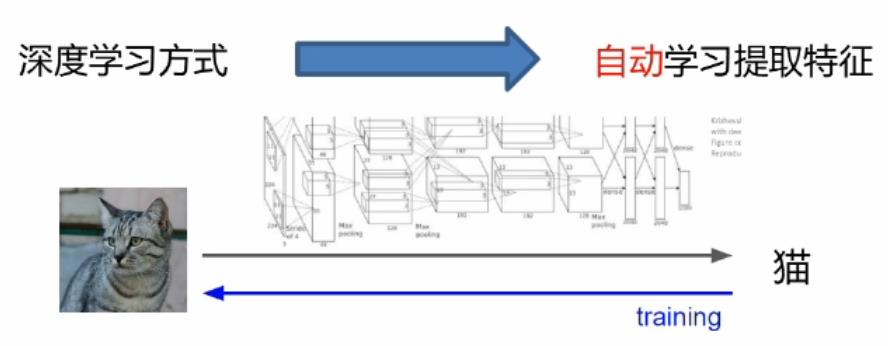
我们可以通过深度学习模型进行自动特征提取，直接从像素进行特征提取，然后去学习，学习之后然后再反向传播后去修正各个模块和提取的方式。这就相当于从头到尾它是一个联通的，不想传统的机器学习那样提取特征后，特征可能是好的也可能是坏的，对后面的学习无法进行修正。因此能够自学习自修正是深度学习的一个非常大的优势之一。深度学习最核心的在于分工与合作，以下图举例说明：

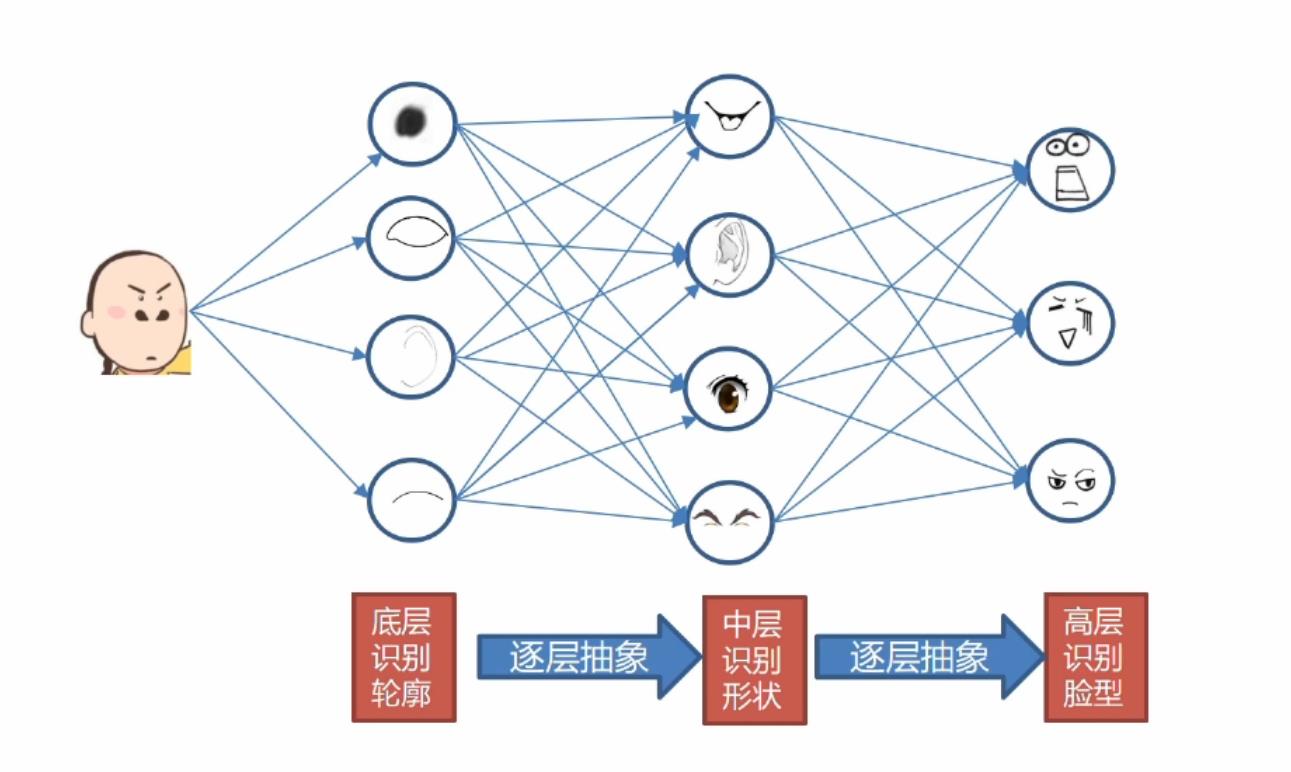
对于这样一个人脸图像，首先我们进行底层的轮廓识别，得到这些最基本特征，然后逐层抽象之后可能得到耳朵，鼻子，眼睛等这些中层识别形状特征。然后再进行逐层的抽象就会变成高级的脸部特征，比如笑脸和哭脸等特征，这就是深度学习最重要的分工和合作，逐层提取出不同的特征，然后重新组合得到更高级更抽象的特征。

损失函数与梯度下降

比如我们经常用到的均方误差分析法（最小二乘法）和交叉熵损失法（对数极大似然）：
均方误差损失(最小二乘法) ：该损失函数用于度量输出值范围为实数的回归任务。

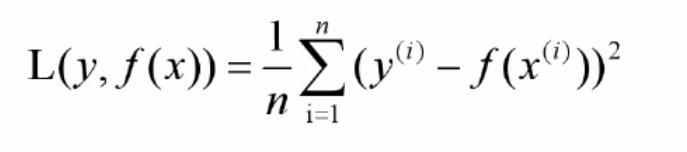
交叉熵损失(对数极大似然):该损失函数用于度量输出值范围为(0, 1)概率的分类任务。

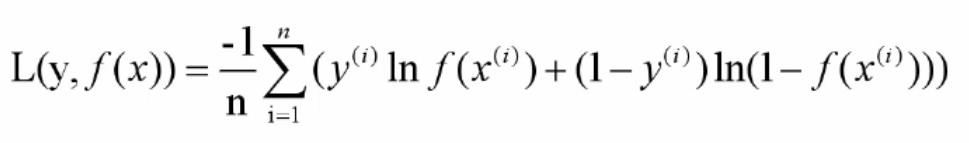
综上所述：我们损失函数的核心目的就是降低损失，那么如何降低损失函数？我们需要用到梯度下降法等来降低损失函数。

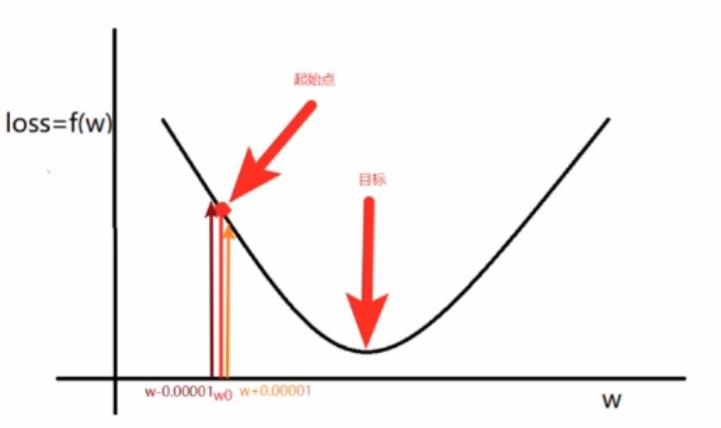
对于上述图中的损失函数（均方误差函数），如图中所示的起始点与目标点，那么我们如何去降低它呢？我们可以在起始点处进行试探，如以下梯度公式：

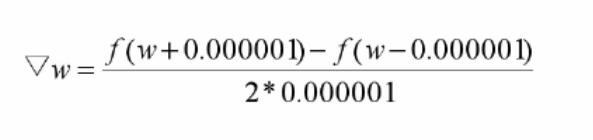
所谓梯度就是下降最快的方向，根据正负确定向左还是向右，最终在目标值处附近徘徊震荡并趋向于最优值，说白了其实就是就是确定损失函数降低的方向（增加还是减少参数），至于一次要走多少距离，一般用α表示，也就是学习率，一般由认为设置。

反向传播算法推导

下图为一个简单的数学链式求导的一个问题：J（a，b，c）=3（a+bc），u=a+v，v=bc，求a，b，c 各自的偏导数。求得结果如下图所示：

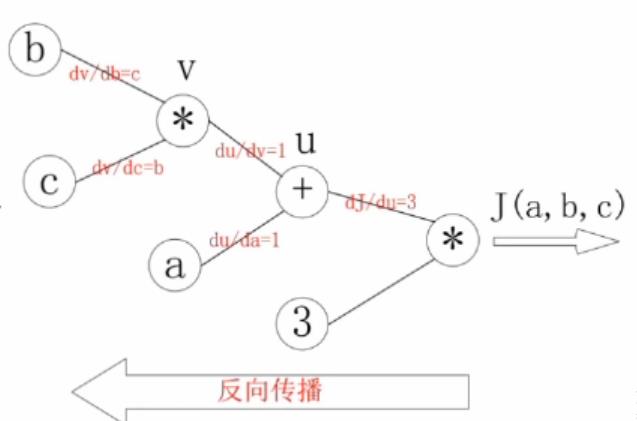
a，b，c 各自的偏导数就等于反向的梯度连接线相乘
dJ\\da= 31 dJ\\db= 31c dJ\\dc=b1*3
总结：反向传播就是复合函数的链式求导法则的应用。

批量标准化介绍

为什么要进行批量标准化？
对于量纲不一致的数据，按照一定的规则，进行一个批量处理，这样的好处就是可以加快神经网络的训练速度，提高模型的精度。

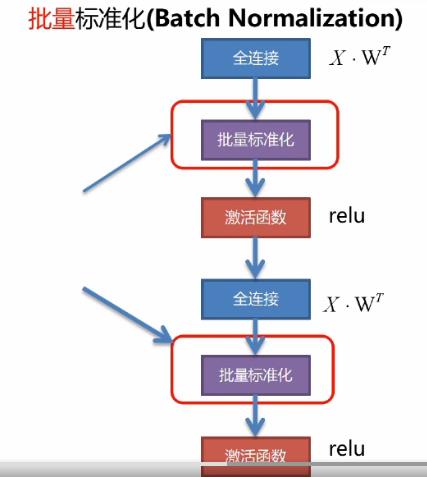
上图为深度学习网络的一个基本框架，全连接层实质上就是一个映射变换，然后放入激活函数中进行激活，再进入到下一个连接层，这样一层一层的进行传播。每一个连接层就是转化后的特征，也都需要去进行批量标准化。为了配合随机梯度下降，我们使用批量采样数据的均值与标准差。该方法极大的降低了深度学习训练的难度！

Dropout介绍

Dropout（最常用的深度学习正则化措施）
下图分别为深度学习的全连接模型和经过Dropout后的深度学习模型


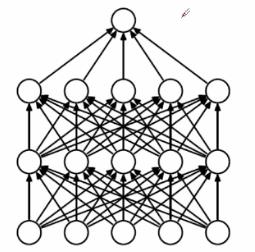
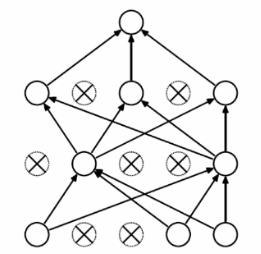
如第二个图所：Dropout实质上就是每一次选取部分神经元进行传播计算。
Dropout：训练时：每次迭代只随机激活一定数量的神经元进行计算。
测试时：激活所有神经元进行计算。
计算过程：
1.生成掩码
训练过程：
以p的概率随机产生0，1数；
mask={0 1 0 0 1 0 0 1 0}；其中0表示抑制，1表示激活。
测试过程：
mask={1 1 1 1 1 1 1 1 1};
计算过程：
out = mask*ReLu

GAN原始论文理解

生成对抗网络基本介绍

生成对抗网络由GoodFellow在2014年首次提出，是未来深度学习最具潜力与突破性的想法。在数字手写体生成，图像风格转换，图像修复等领域具有很广阔的前景。GAN的核心思想就是最小最大游戏（零和博弈），游戏双方为判别器跟生成器，生成器就是学习伪造数据，判别器就是判别数据的真实性，判别数据是生成器生成的还是原本真实的数据。为了胜利，它们不断优化自我不断提高各自的生成能力和判别能力。最终生成器可以以假乱真生成真实的数据。

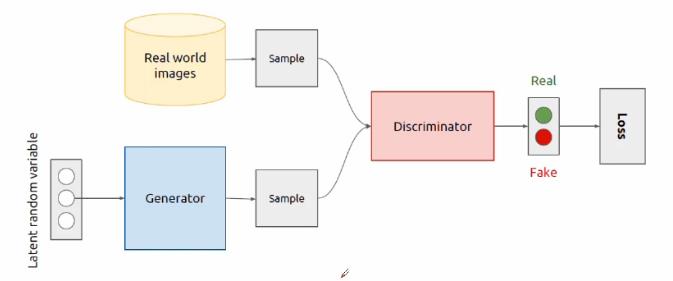
生成器跟判别器为两个分开独立的神经网络，生成器用来学习生成数据，随机的噪声作为生成器一开始的输入数据，经过生成器的传播形成一定的采样数据。判别器用来判别数据的好坏与真实性。数据的来源一部分来自对真实数据的采样，另一部分来自于生成器生成的数据。对真实的数据标记为”1“，代表数据是真实的，然后进行一个前向传播，然后选取同等数量的生成器生成的数据标记为”0“，然后交给判别器进行一个前向传播，就可以计算到一些损失值，然后再进行反向传播。特别注意的是：在训练判别器的时候应锁住生成器，反之亦然。在训练生成器的时候，不训练判别器，判别器仅仅提供梯度，不提供权重的更新。

生成对抗网络理论推导

数据生成

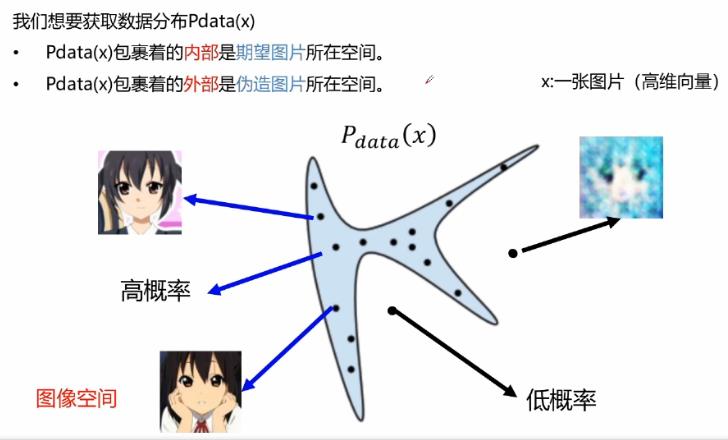
Pdata（x）外部的空间是一些伪造的图片，由对抗网络所生成的一些数据。GAN的目标其实就是找到Pdata（x）这样一个数据空间，在它的内部生成一些足够真实的数据。

我们并不知道数据分布Pdata（x）是什么样子，但是我们可以确信我们的数据来源于Pdata（x）。

PG（x）是我们生成模型生成的数据分布，我们期望它生成的数据和Pdata（x）尽可能的相似。

生成器——制造数据

生成器（generator）G是一个神经网络，该网络可以生成数据。

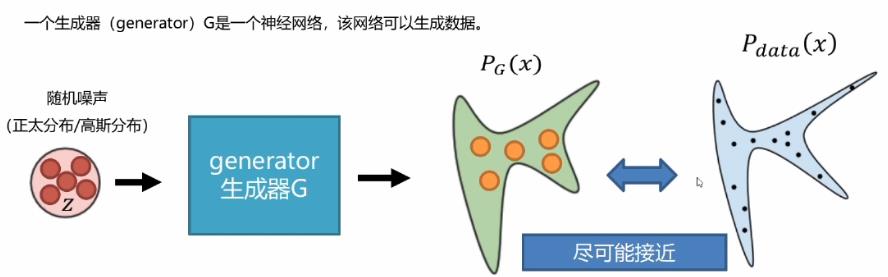
计算差异

生成器生成的数据PG（x）尽可能要与Pdata（x）相近，接近之后才能仿造真实的数据，但是问题是如何去衡量和计算它们之间的差异呢？

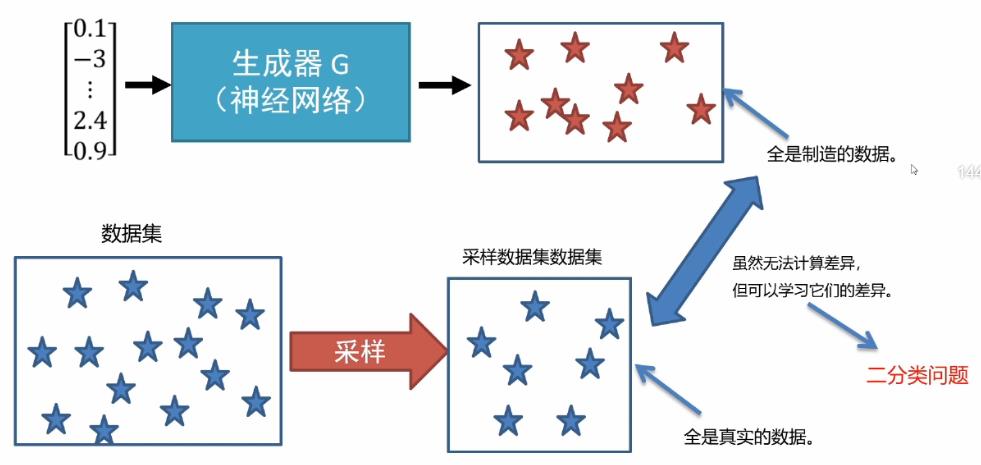
第一部分生成器对随机噪声进行传播计算得到伪造的数据，这是我们已知的。真实的数据也就是已经存在的数据集，对其进行采样后一部分数据得到真实的数据集。对于两个数据之间的差异我们可以进行学习，可以归为一个简单的二分类问题。

判别器——学习数据差异性

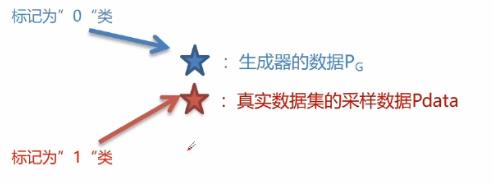
将生成器制造的数据跟采样数据合在一起，组合成了一个二分类数据集。然后放入判别器的神经网络中进行训练从而达成目的。我们可以使用极大似然估计这样的损失函数用来学习二分类学习任务。

上述公式中，红色部分来源于真实的数据，所以我们的损失值logD（x），D（x）期望输出1，生成器标记为”0“类，因此损失值用log（1-D（x））来表示。将二分类数据集送给判别器，如果这个数据集差异性较小，那么判别器将难以判别，训练完后还是损失值较大，很难降低。如果这个数据集本身差异性就很大，即使通过判别器简单的训练后就非常容易判别，那么就是最终判别器的损失值较小。所以就是说，训练到最优的时候，损失值越小，数据的差异性就越大。接下来用公式举例说明：


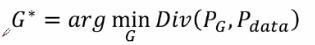
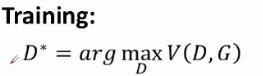
我们的目标是学习一个生成器G*，它的目的是最小化Pg和Pdata之间的差异性，那么最小化G的话，我们就需要训练一个最佳的D*，D的任务就是要最大化真实书记和伪造数据之间的差异性，对于判别器所提供的一个差异然后再进行一个生成器的训练。

最大化差异推导

判别器的目标就是最大化数据的差异，我们可以使用以下交叉熵损失函数：

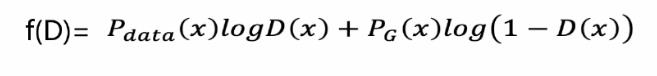
对此公式进行简化后可得：

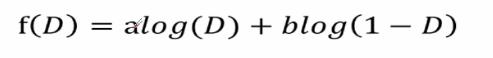
我们的目的是求最大化差异也就是求f（D）的极值，那么可得f（D）函数的梯度就等于0，

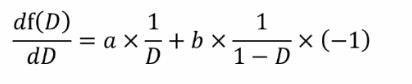
整体后可得：


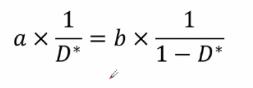
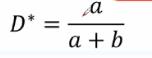
可得最佳的判别器D*(x)的表达式如下：

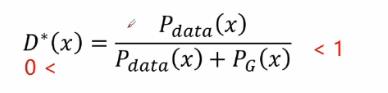
然后将D*(x)带入判别器的一个交叉熵损失函数中：
交叉熵损失函数：

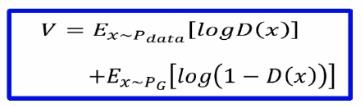
带入后可得以下等式并推导可得GAN用JS散度描述的一个损失函数（Jensen-Shannon divergence）：

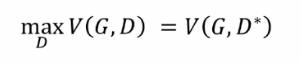
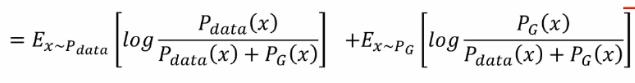
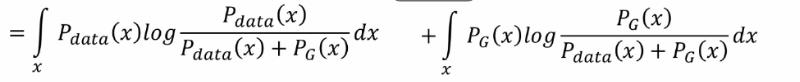
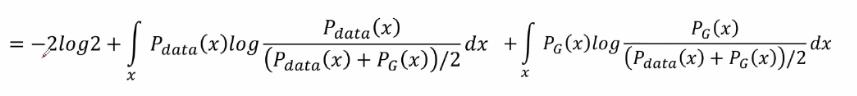
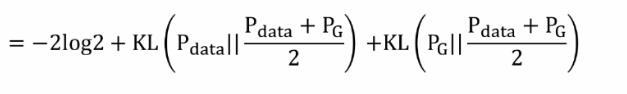
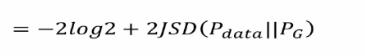
优化过程

生成对抗网络的代价函数：

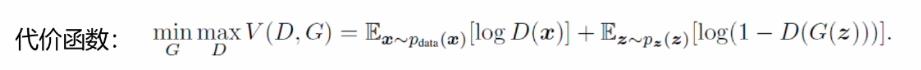
它是一个最大化最小化的过程，首先要最大化判别器的差异性，他要去判别生成数据跟真实数据之间的差异，在训练较好的情况之后，接下来就最下化生成器的损失，生成器生成的数据要和真实数据尽可能的高度相似，然而判别器要尽可能的进行区分真实数据和生成数据，因此两者之间就产生了一个对抗的关系。

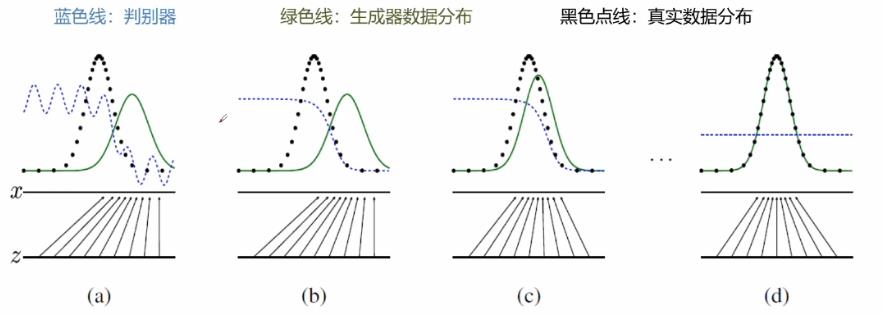
GAN原始论文算法步骤详述

判别器训练算法

生成器训练算法

GAN存在的问题

可解释性非常差

所学到的数据分布Pg(G)，没有显示的表达式。它只是一个黑盒子一样的映射函数： 输入是一个随机变量，输出想要的一个数据分布。

训练不稳定

难以保持生成器与判别器的平衡

优化震荡现象

生成器容易产生模式崩溃（Mode collapse）

举个生成数字图像的例子：生成器要生成0-9之间的数字，而判别器只是要判断生成器生成的数据像不像真实数据。比如”1“是非常容易生成的一个数字，那么生成器可能就会拼命的去生成更多的真实的”1“，从而判别器就难以判别。对于其他的复杂一点的数字比如”8“，”9“，生成器可能就干脆不生成了，从而避免犯错，这就是生成器的一个大问题，我们的希望是生成0-9的数字，然而最终就会导致这些问题出现。

数字手写体生成应用

数字图像生成介绍

生成器网络结构初始化代码

    def _init_gen(self):
        """
        初始化生成器网络结构
        网络结构 例如[noise_dim,100]*[100,100]*[100,gen_dim]
        :return: 生成数据op
        """
        self.gen_x = tf.placeholder(dtype=tf.float32, shape=[None, self.noise_dim], name="gen_x")
        # 构造生成器输入层
        active = tf.nn.relu(tf.matmul(self.gen_x, self.w_g_list[0]) + self.b_g_list[0])
        # 构造生成器隐藏层
        for i in range(len(self.gen_hidden) - 1):
            active = tf.nn.relu(tf.matmul(active, self.w_g_list[i + 1]) + self.b_g_list[i + 1])
        # 构造输出层
        out_logis = tf.matmul(active, self.w_g_list[-1]) + self.b_g_list[-1]
        g_out = tf.nn.sigmoid(out_logis)
        return g_out

判别器网络结构初始化代码

    def _init_dicriminator(self, input_op):
        """
        初始化判别器网络结构
        网络结构 例如：[gen_dim,100]*[100,100]*[100,1]
        :param input_op: 输入op
        :return: 判别器op
        """
        # 构造判别器输入层
        active = tf.nn.relu(tf.matmul(input_op, self.w_d_list[0]) + self.b_d_list[0])
        # 构造判别器隐藏层
        for i in range(len(self.d_hidden) - 1):
            active = tf.nn.relu(tf.matmul(active, self.w_d_list[i + 1]) + self.b_d_list[i + 1])
        # 构造判别器输出层
        out_logis = tf.matmul(active, self.w_d_list[-1]) + self.b_d_list[-1]
        return out_logis

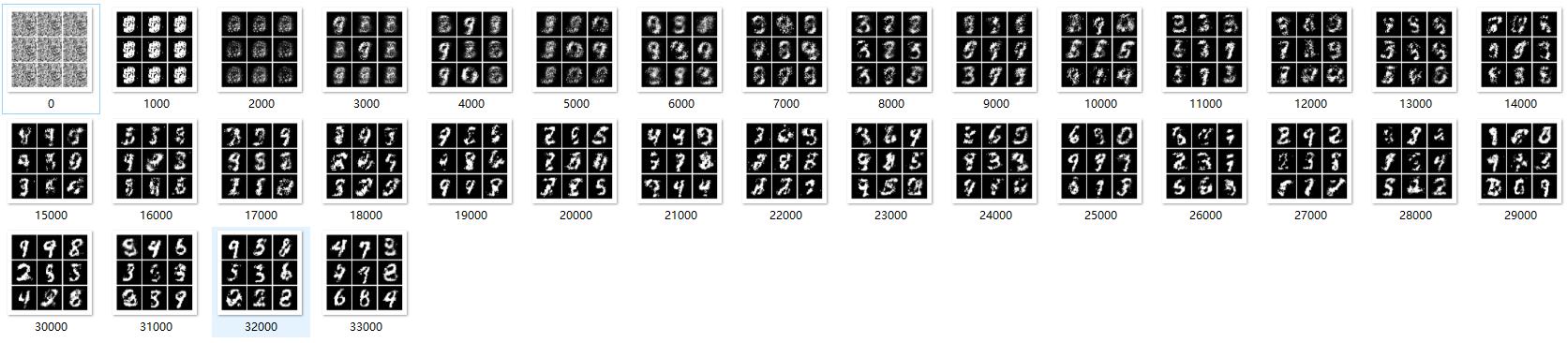
仿真结果

其他

本文是建立在第一篇GAN的原始论文——《GenerativeAdversarialNets》的基础之上进行的一个总结，并借鉴别人的代码对原文的算法进行一个简单的复现，接下来会继续学习并整理深度卷积生成对抗网络（DCGAN），Wasserstein GAN（WGAN），LSGAN，Improved Training of Wasserstein GAN，CGAN，CycleGAN等GAN的各种变形。
本文代码：链接：https://pan.baidu.com/s/19C68rjnOxUkEEJxnKkYo7w
提取码：o9vp
关注！关注！关注！关注！关注！关注！关注！关注！关注！