DFS+剪枝Aw842.排列数 & Aw843.N-皇后问题

Posted 2021-06-26 _BitterSweet

DFS练习

• aw842.排列数
• • 题目描述
  • 思路分析
  • 代码实现
• aw843.N-皇后问题
• • 题目描述
  • 思路分析
  • 代码实现

aw842.排列数

题目描述

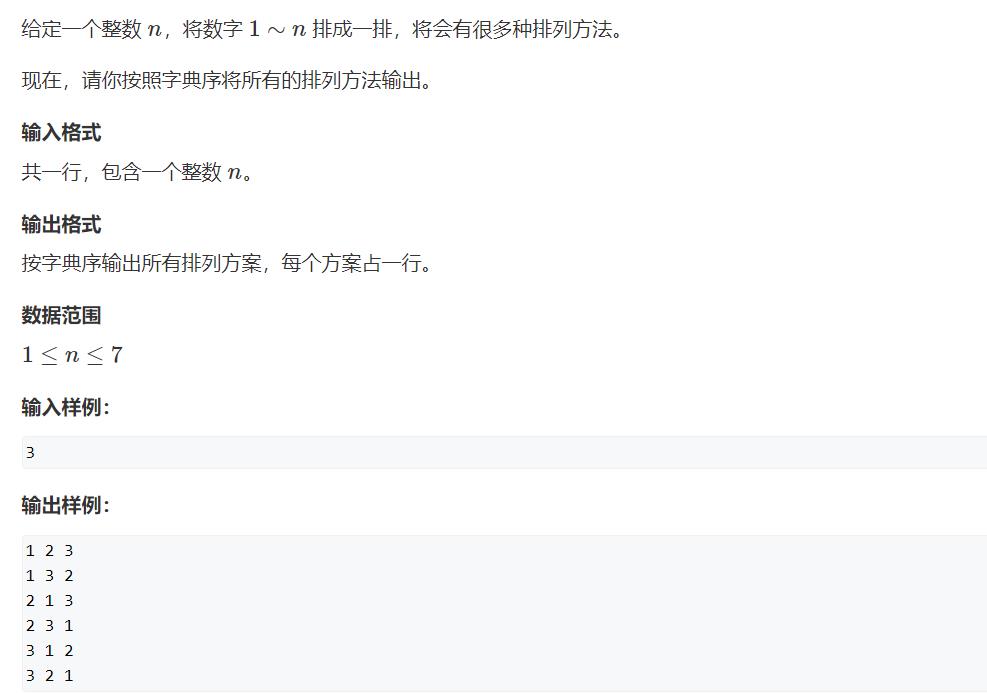
题目链接：https://www.acwing.com/problem/content/844/

思路分析

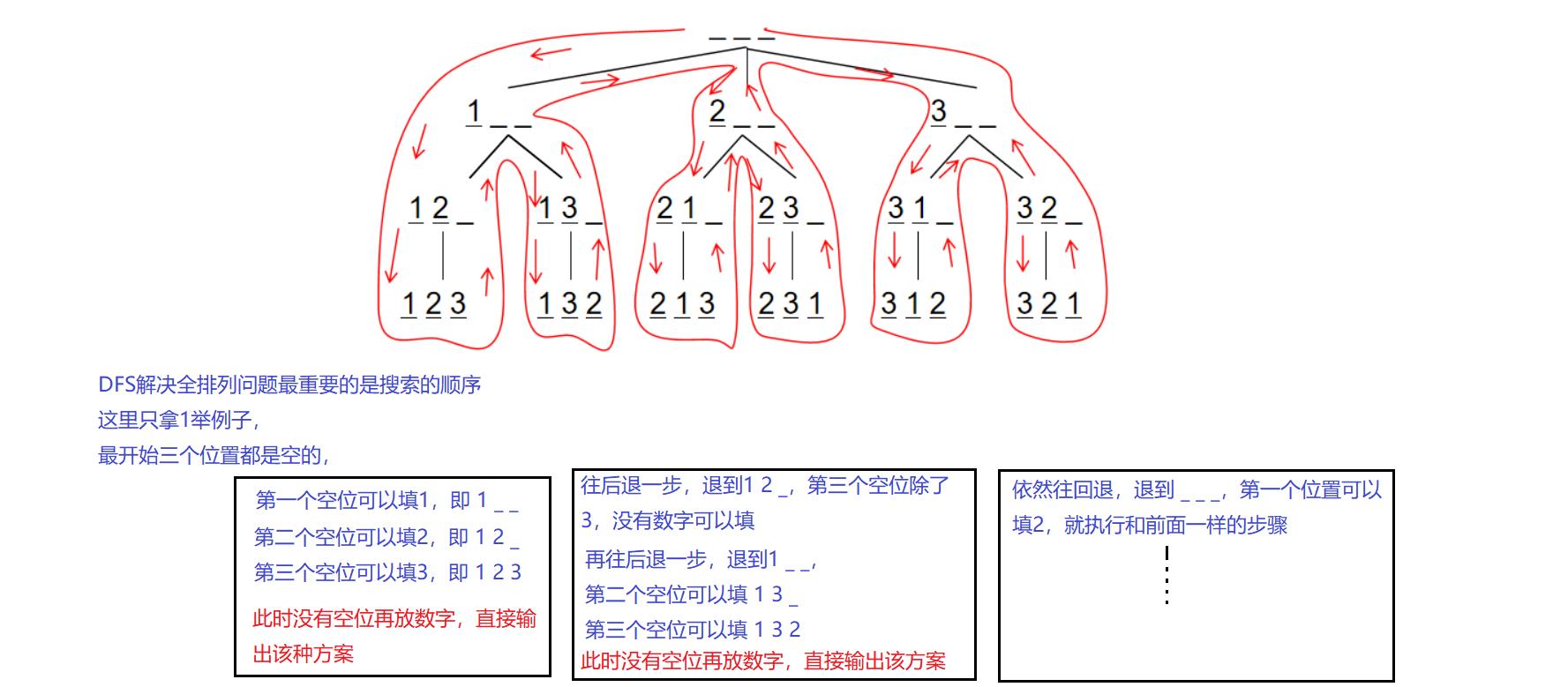
代码实现

#include<iostream>
using namespace std;
const int N = 10; 
int n;
int path[N];//保存序列
bool state[N];//位置是否被用过


void dfs(int u)
{
   if(u > n)//数字填完了则输出
   {
       for(int i = 1; i <= n; i++)
            cout << path[i] << " "; //输出方案
        cout << endl;
   }
   //空位上可以选择的数字为1~n
   for(int i = 1; i <= n; i++)
   {
       if(!state[i])//如果i位置没有被用过
       {
           path[u] = i;//放入空位
           state[i] = true;//数组被用，记为true
           dfs(u + 1);//填写下一个位置
           state[i] = false;//回溯
       }
   }
}

int main()
{
    cin >> n;
    dfs(1);
    return 0;
}

aw843.N-皇后问题

题目描述

题目链接：https://www.acwing.com/problem/content/description/845/

思路分析

---

• 思路一：按行枚举
  

---

• 思路二：按元素个数枚举
  

---

代码实现

• 按行搜索

#include<iostream>
using namespace std;

const int N = 20;
int n;
bool col[N],dg[N],udg[N];//col：列 dg：对角线 udg：反对角线
char g[N][N]; //用来存路径

void dfs(int u)
{
    if(u == n) //表示已经搜了n行，则输出这条路径
    {
        for(int i = 0; i < n; i++) puts(g[i]);
        puts("");
        return;
    }
    
    //对n个位置按行搜索
    for(int i = 0; i < n; i++)
    {
        //剪枝：对于不满足要求的点，不再往下搜索
        if(!col[i] && !dg[u + i] && !udg[n - u + i])
        {
            g[u][i] = 'Q';
            col[i] = dg[u + i] = udg[n - u + i] = true;
            dfs(u + 1);
            col[i] = dg[u + i] = udg[n - u + i] = false;//恢复现场
            g[u][i] = '.';
        }
    }
}

int main()
{
    cin >> n;
    for(int i = 0; i < n; i++)
        for(int j = 0; j < n; j++)
            g[i][j] = '.';
    
    dfs(0);
    return 0;
}

• 按元素搜索

#include <iostream>
using namespace std;
const int N = 20;

int n;
char g[N][N];
bool row[N], col[N], dg[N], udg[N]; // 因为是一个个搜索，所以加了row

// s表示已经放上去的皇后个数
void dfs(int x, int y, int s)
{
    // 处理超出边界的情况
    if (y == n) y = 0, x ++ ;

    if (x == n) // x==n说明已经枚举完n^2个位置了
    { 
        if (s == n) // s==n说明成功放上去了n个皇后
        { 
        	//输出这组解
            for (int i = 0; i < n; i ++ ) puts(g[i]);
            puts("");
        }
        return;
    }

    // 分支1：放皇后
    if (!row[x] && !col[y] && !dg[x + y] && !udg[x - y + n]) 
    {
        g[x][y] = 'Q';
        row[x] = col[y] = dg[x + y] = udg[x - y + n] = true;
        dfs(x, y + 1, s + 1);
        row[x] = col[y] = dg[x + y] = udg[x - y + n] = false;
        g[x][y] = '.';
    }

    // 分支2：不放皇后
    dfs(x, y + 1, s);
}


int main() 
{
    cin >> n;
    for (int i = 0; i < n; i ++ )
        for (int j = 0; j < n; j ++ )
            g[i][j] = '.';

    dfs(0, 0, 0);

    return 0;
}

---

• 思路一的效率更高一些

---