《通信原理》复习笔记3----第三章随机过程(重点与难点)
Posted 遗忘丶
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了《通信原理》复习笔记3----第三章随机过程(重点与难点)相关的知识,希望对你有一定的参考价值。
系列文章链接目录
一、《通信原理》复习笔记1----第一章绪论
二、《通信原理》复习笔记1----第一章绪论相关例题
三、《通信原理》复习笔记3----第三章随机过程(重点与难点)
前言
本章的复习重点在于,会求随机过程的数字特征,掌握如何判断平稳随机过程,理解各态历经性,掌握平稳过程的功率谱密度计算。记忆高斯随机过程的重要性质以及记忆窄带随机过程的几个重要结论。
一、随机过程的数字特征
随机信号:信号的某个或几个参数不能预知或不能完全预知的信号
随机噪声:不能预测的噪声
随机过程:随机信号和噪声统称为随机过程
随机过程数字特征最常用的是均值、方差和相关函数。
1.1 均值(数学期望)
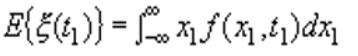
⮚数学期望的物理意义:信号或噪声的直流分量。
1.2 方差
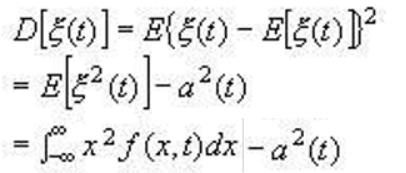
⮚方差的物理意义:信号或噪声的交流功率。
1.3自相关函数
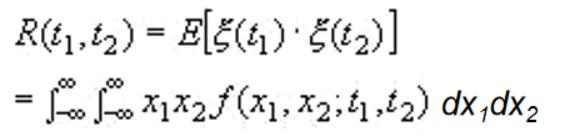
用途:
a.用来判断广义平稳;
b.用来求解随机过程的功率谱密度及平均功率。
二、平稳随机过程
2.1 狭义平稳随机过程(严平稳随机过程)
2.1.1 狭义(严)平稳随机过程定义与含义

2.1.2 平稳随机过程的数字特征(判定平稳随机过程的依据)
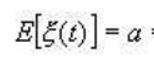
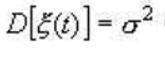
总结如下:

2.2 广义平稳随机过程

狭义平稳一定是广义平稳的,广义平稳不一定是狭义平稳。
2.3 各态历经的平稳随机过程
2.3.1 各态历经性
⮚“时间平均”代替“统计(逻辑)平均。”
⮚一个随机过程的均值和自相关函数都具有各态历经性,则称该随机过程具有各态历经性。

只有平稳随机过程才具有各态历经性,即各态历经的随机过程一定是平稳的,而平稳的随机过程则需要满足一定的条件才是各态历经的。
2.4 平稳过程的自相关函数
平稳随机过程的自相关函数和时间t无关,而只与时间间隔τ有关,即
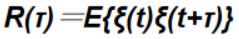
2.4.1平稳随机过程自相关函数的五个主要性质
①R(0)=E[ξ2(t)] , 表示R(0)为ξ(t)的均方值的平均功率。
②对偶性:R(τ)=R(-τ) ,表示自相关函数R(τ)是τ的偶函数。
③有界性:|R(τ)|≤ R(0) ,表示R(τ)的上界。即自相关函数R(τ)在τ=0时取最大值。
④R(∞ )=E2 [ξ(t)] ,表示R(∞ )是ξ(t)的直流功率。
⑤R(0) - R(∞)=σ2,σ2是方差,表示平稳过程ξ(t)的交流功率,当均值为0时有R(0)=σ2。
2.5 平稳过程的功率谱密度
2.5.1 功率谱密度概念
从频率的角度描述ξ(t)的统计规律的最主要的数字特征。它的物理意义表示ξ(t)的平均功率关于频率的分布。
2.5.2 功率谱密度的计算

2.5.3 功率谱密度的性质

三、高斯随机过程
3.1高斯随机过程定义(又称正态随机过程)
若随机过程ξ(t)的任意n维概率密度函数都服从正态分布,则称它为高斯过程。
3.2高斯随机过程重要性质
①高斯过程的n维分布只依赖各个随机变量的均值、方差和归一化协方差;
②高斯过程若是广义平稳随机过程,则又是狭义平稳随机过程;
③若高斯过程中的随机变量之间互不相关,则它们也是相互独立的;
④若干个高斯过程的代数和的过程仍是高斯过程;
⑤高斯过程经过线形变换后的过程仍是高斯过程。
四、随机过程通过线性系统
结论:平稳随机过程经线性系统传输后,输出仍然为平稳随机过程。
推论:
(1)输入是各态历经的随机过程, 输出也是各态历经的随机过程。
(2)输入是高斯过程,输出也是高斯过程,只是均值和方差发生了变化。
五、窄带随机过程
窄带随机过程ξ(t)可表示为:
ξ(t) = ξc(t) coswct - ξs(t) sinwct
其中,
同相分量ξc(t)=αξ(t) cosφξ(t)
正交分量ξs(t)=αξ(t) sinφξ(t)
窄带过程ξ(t)是平稳的,则ξc(t)与ξs(t)也必然是平稳的。
一个均值为0的窄带平稳高斯过程ξ(t),它的同相分量ξc(t)和正交分量ξs(t)同样是平稳高斯过程,而且均值为0,方差也相同。此外,在同一时刻上得到的ξc和ξs是互不相关的或统计独立的。
结论:
一个均值为零、方差为σ2的平稳高斯窄带随机过程:
①其包络αξ(t)的一维分布服从瑞利分布;
②相位Ψξ(t)的一维分布服从均匀分布;
③αξ(t)与Ψξ(t)统计独立;
④它的同相分量和正交分量同样是平稳高斯过程,且均值为零,方差相同。
六、正弦波加窄带随机过程
正弦波加窄带高斯过程的包络f(z) 服从莱斯分布。
以上是关于《通信原理》复习笔记3----第三章随机过程(重点与难点)的主要内容,如果未能解决你的问题,请参考以下文章