数据结构—— 散列查找：散列表的性能分析

Posted 大彤小忆

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了数据结构—— 散列查找：散列表的性能分析相关的知识，希望对你有一定的参考价值。

数据结构系列内容的学习目录 → \\rightarrow →浙大版数据结构学习系列内容汇总。

4. 散列表的性能分析

   ⋆ \\star ⋆ 平均查找长度（ASL）用来度量散列表查找效率：成功、不成功。
   ⋆ \\star ⋆ 关键词的比较次数，取决于产生冲突的多少。
   影响产生冲突多少有以下三个因素：
    (1）散列函数是否均匀；
    (2）处理冲突的方法；
    (3）散列表的装填因子α。
   分析： 不同冲突处理方法、装填因子对效率的影响。

4.1 线性探测法的查找性能

  可以证明，线性探测法的期望探测次数满足下列公式：
p = { 1 2 [ 1 + 1 ( 1 − α ) 2 ] （ 对 插 入 和 不 成 功 查 找 而 言 ） 1 2 [ 1 + 1 1 − α ]       （ 对 成 功 查 找 而 言 ）                           p=\\left\\{\\begin{matrix} \\frac{1}{2}\\left [ 1+\\frac{1}{(1-\\alpha)^{2} } \\right ]（对插入和不成功查找而言） \\\\ \\frac{1}{2}\\left [ 1+\\frac{1}{1-\\alpha } \\right ] \\ _{}\\ _{}\\ _{}（对成功查找而言）\\ _{}\\ _{}\\ _{}\\ _{}\\ _{}\\ _{}\\ _{}\\ _{}\\ _{}\\ _{}\\ _{}\\ _{}\\ _{} \\end{matrix}\\right. p={21​[1+(1−α)21​]（对插入和不成功查找而言）21​[1+1−α1​] ​ ​ ​（对成功查找而言） ​ ​ ​ ​ ​ ​ ​ ​ ​ ​ ​ ​ ​​  当a = 0.5时，
   ∘ \\circ ∘ 插入操作和不成功查找的期望ASLu = 0.5*(1+1/(1-0.5) 2 ^{2} 2 )= 2.5次
   ∘ \\circ ∘ 成功查找的期望ASLs = 0.5*(1+1/(1-0.5) ) = 1.5次

在这里插入图片描述
  a = 9/13 = 0.69，于是
   ∘ \\circ ∘ 期望ASLu = 0.5*(1+1/(1-0.69) 2 ^{2} 2 ) = 5.70次
   ∘ \\circ ∘ 期望ASLs = 0.5*(1+1/(1-0.69) ) = 2.11次（实际计算ASLs =2.56)

4.2 平方探测法和双散列探测法的查找性能

  可以证明，平方探测法和双散列探测法探测次数满足下列公式：
p = { 1 1 − α   （ 对 插 入 和 不 成 功 查 找 而 言 ） − 1 α l n ( 1 − α )   （ 对 成 功 查 找 而 言 ） p=\\left\\{\\begin{matrix} \\frac{1}{1-\\alpha} \\ _{}（对插入和不成功查找而言） \\\\ -\\frac{1}{\\alpha}ln(1-\\alpha) \\ _{}（对成功查找而言） \\end{matrix}\\right. p={1−α1​ ​（对插入和不成功查找而言）−α1​ln(1−α) ​（对成功查找而言）​  当a = 0.5时，
   ∘ \\circ ∘ 插入操作和不成功查找的期望ASLu = 1/(1-0.5) = 2次
   ∘ \\circ ∘ 成功查找的期望ASLs = -1/0.5* In(1-0.5) = 1.39次

在这里插入图片描述
  a = 9/11 = 0.82，于是
   ∘ \\circ ∘ 期望ASLu = 1/(1-0.82) = 5.56次
   ∘ \\circ ∘ 期望ASLs = -1/0.5* In(1-0.5) = 2.09次（例中ASLs = 2)

  期望探测次数与装填因子α的关系如下图所示。

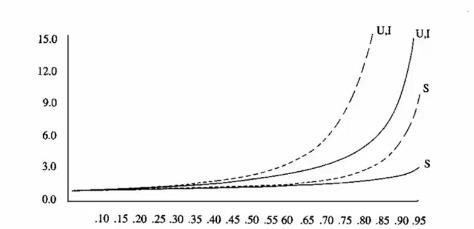
在这里插入图片描述
  上图中，线性探测法（虚线)、双散列探测法（实线)、U表示不成功查找、I表示插入、S表示成功查找。
   ⋆ \\star ⋆ 当装填因子a<0.5的时候，各种探测法的期望探测次数都不大，也比较接近。
   ⋆ \\star ⋆ 随着α的增大，线性探测法的期望探测次数增加较快，不成功查找和插入操作的期望探测次数比成功查找的期望探测次数要大。
   ⋆ \\star ⋆ 合理的的最大装入因子α应该不超过0.85。

4.3 分离链接法的查找性能

  所有地址链表的平均长度定义成装填因子α，α有可能超过1。
  不难证明：其期望探测次数p为：
p = { α + e − α   （ 对 插 入 和 不 成 功 查 找 而 言 ） 1 + α 2   （ 对 成 功 查 找 而 言 ）                                 p=\\left\\{\\begin{matrix} \\alpha+e^{-\\alpha} \\ _{}（对插入和不成功查找而言） \\\\ 1+\\frac{\\alpha}{2}\\ _{}（对成功查找而言）\\ _{}\\ _{}\\ _{}\\ _{}\\ _{}\\ _{}\\ _{}\\ _{}\\ _{}\\ _{}\\ _{}\\ _{}\\ _{}\\ _{}\\ _{}\\ _{} \\end{matrix}\\right. p={α+e−α ​（对插入和不成功查找而言）1+2α​ ​（对成功查找而言） ​ ​ ​ ​ ​ ​ ​ ​ ​ ​ ​ ​ ​ ​ ​ ​​  当a = 1时，
   ∘ \\circ ∘ 插入操作和不成功查找的期望ASLu= 1+e − 1 ^{-1} −1 = 1.37次
   ∘ \\circ ∘ 成功查找的期望ASLs = 1+1/2 = 1.5次

  前面例子14个元素分布在11个单链表中，所以α = 14/11 = 1.27，故
   ∘ \\circ ∘ 期望ASLu = 1.27+e − 1.27 ^{-1.27} −1.27 = 1.55次
   ∘ \\circ ∘ 期望ASLs = 1+1.27/2 =1.64次（例中ASLs = 1.36)

   ⋆ \\star ⋆ 选择合适的h(key)，散列法的查找效率期望是常数 O ( 1 ) O(1) O(1)，它几乎与关键字的空间的大小n无关！也适合于关键字直接比较计算量大的问题。
   ⋆ \\star ⋆ 它是以较小的α为前提。因此，散列方法是一个以空间换时间。
   ⋆ \\star ⋆ 散列方法的存储对关键字是随机的，不便于顺序查找关键字，也不适合于范围查找，或最大值最小值查找。

4.4 开放地址法 vs 分离链法

   开放地址法： 散列表是一个数组，存储效率高，随机查找。
          散列表有“聚集”现象。
   分离链法： 散列表是顺序存储和链式存储的结合，链表部分的存储效率和查找效率都比较低。
           关键字删除不需要“懒惰删除”法，从而没有存储“垃圾”。
           太小的α可能导致空间浪费，大的α又将付出更多的时间代价。不均匀的链表长度导致时间效率的严重下降。

以上是关于数据结构—— 散列查找：散列表的性能分析的主要内容，如果未能解决你的问题，请参考以下文章

jdk源码分析——HashMap

Python 常用查找数据结构及算法

数据结构学习笔记——查找算法（线性查找散列查找）

数据结构学习笔记——查找算法（线性查找散列查找）

数据结构—— 散列查找：散列表

散列表的平均查找长度怎么计算？