Python|递归法判断平衡二叉树

Posted 2021-06-25 算法与编程之美

本文首发于微信公众号："算法与编程之美"，欢迎关注，及时了解更多此系列文章。

问题描述

给定一个二叉树，判断它是否是高度平衡的二叉树。

本题中，一棵高度平衡二叉树定义为：一个二叉树每个节点 的左右两个子树的高度差的绝对值不超过 1 。

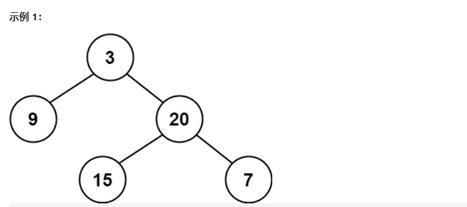
输入：root = [3, 9, 20, null, null,15, 7]

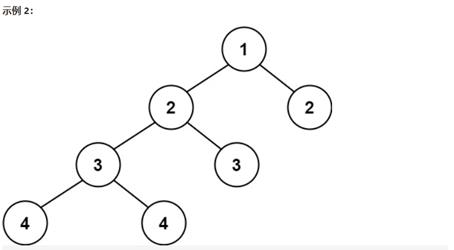
root = [1, 2, 2, 3, 3, null,null, 4, 4]

root = []

输出：true

     false 

     true

解决方案

首先要先知道平衡二叉树的是什么，二叉树是数据结构中由n个结点组成的有限集合，二叉树是有序树，有左右两子树；平衡二叉树就是二叉树的每个结点的高度差不会超过1并且只会在（-1,0,1）三个范围中的二叉树，所以在判断时可以使用递归的方式去判断是否为平衡二叉树，递归的方式可以是自上而下或者自下而上，这里使用的是自上而下。先定义一个新的函数，将节点分为空与非空，然后对二叉树进行遍历，计算左右子树的高度，如果左右子树的高度差在范围内，就分别递归左右子节点进行判断是否平衡。因为本题是在力扣上做的，前两行的定义函数是力扣自动生成的，但是后面的需要更换函数就可以在pychram上运行。

代码中的root是二叉树的根节点，left与right是左右子树

结语

要解决本题需要学习数据结构中的二叉树的相关知识，包括先中后序遍历等对二叉树的变换以及应用，本文的代码也比较难懂，也要对函数有基础使用方法。本次就是用到的递归的方式来解决这个问题。

附件

class Solution:     def isBalanced(self, root: TreeNode) -> bool:         def height (root:TreeNode)-> int:             if not root:                 return 0             return max(height(root.left),height(root.right)) + 1           if not root:             return True         return abs(height(root.left)-height(root.right)) <= 1 and self.isBalanced(root.left) and self.isBalanced(root.right)

实习编辑：衡辉

稿件来源：深度学习与文旅应用实验室（DLETA）