算法: 1143. Longest Common Subsequence最长公共子序列

Posted 2021-06-25 架构师易筋

1143. Longest Common Subsequence

Given two strings text1 and text2, return the length of their longest common subsequence. If there is no common subsequence, return 0.

A subsequence of a string is a new string generated from the original string with some characters (can be none) deleted without changing the relative order of the remaining characters.

For example, “ace” is a subsequence of “abcde”.
A common subsequence of two strings is a subsequence that is common to both strings.

Example 1:

Input: text1 = "abcde", text2 = "ace" 
Output: 3  
Explanation: The longest common subsequence is "ace" and its length is 3.

Example 2:

Input: text1 = "abc", text2 = "abc"
Output: 3
Explanation: The longest common subsequence is "abc" and its length is 3.

Example 3:

Input: text1 = "abc", text2 = "def"
Output: 0
Explanation: There is no such common subsequence, so the result is 0.

Constraints:

1 <= text1.length, text2.length <= 1000
text1 and text2 consist of only lowercase English characters.

动态规划解法

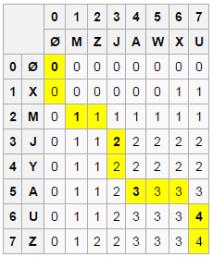
寻找 LCS；
让X是“XMJYAUZ”和Y是“MZJAWXU”。X和之间的最长公共子序列Y是“MJAU”。
下表显示了X和前缀之间的最长公共子序列的长度Y。
ith行和jth列显示之间的LCS的长度X_{1..i}和Y_{1..j}。

class Solution {
    public int longestCommonSubsequence(String text1, String text2) {
        int[][] dp = new int[text1.length() + 1][text2.length() + 1];
        for (int i = 0; i < text1.length(); i++) {
            for (int k = 0; k < text2.length(); k++) {
                if (text1.charAt(i) == text2.charAt(k)) {
                    dp[i + 1][k + 1] = 1 + dp[i][k];
                } else {
                    dp[i + 1][k + 1] = Math.max(dp[i + 1][k], dp[i][k + 1]);
                }
            }
        }
        return dp[text1.length()][text2.length()];
    }
}