面试题打卡——C++版

Posted 2021-06-25 ych9527

文章目录

• • • • 股票价格跨度
      • 买卖股票的最佳时机含手续费
      • 最佳买卖股票时机含冷冻期
      • 买卖股票的最佳时机III
      • 买卖股票的最佳时机IV

股票价格跨度

编写一个 StockSpanner 类，它收集某些股票的每日报价，并返回该股票当日价格的跨度。

今天股票价格的跨度被定义为股票价格小于或等于今天价格的最大连续日数（从今天开始往回数，包括今天）。

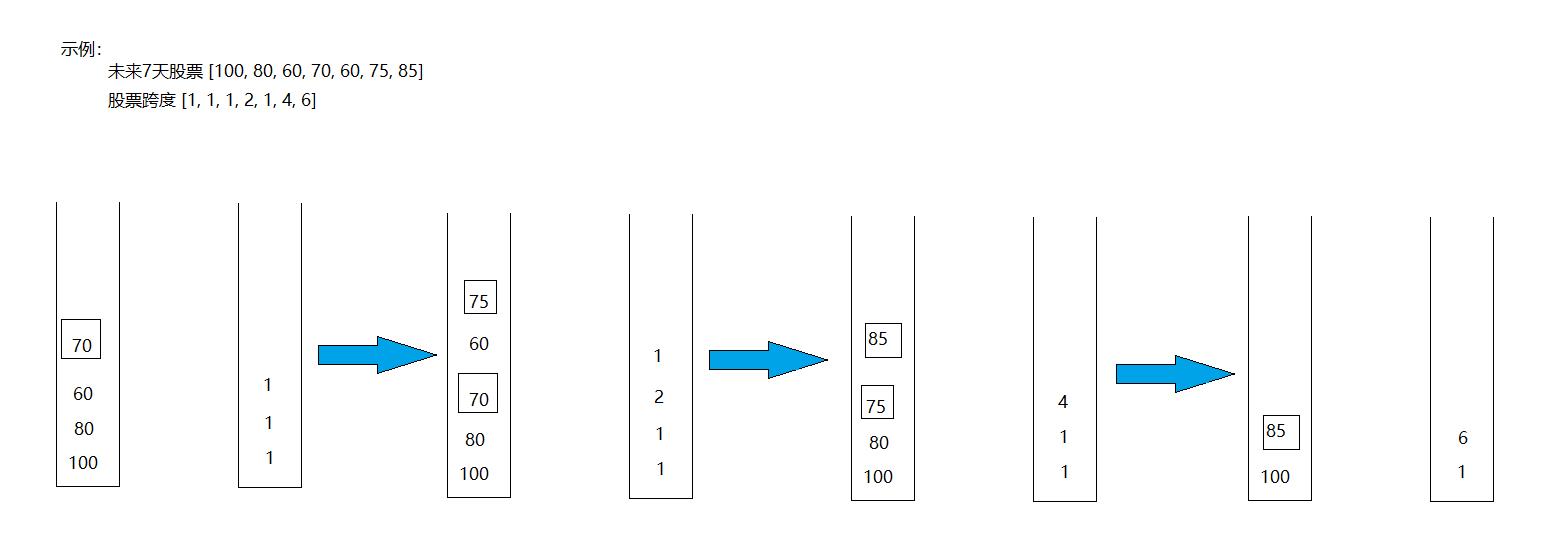
例如，如果未来7天股票的价格是 [100, 80, 60, 70, 60, 75, 85]，那么股票跨度将是 [1, 1, 1, 2, 1, 4, 6]。

题解：

给定两个栈，一个栈存储当前的股票价格，设这个栈为val。
另一个栈存储对应的最大的连续日数，设这个栈为count。

在一个新的元素num进入的时候，设进入count栈的数的大小为sum，初始化sum=1.

num>val.top() -> sum+=count.top() 并且 count和val同时进行出栈动作，这里利用while循环进行比较叠加，这是因为在当前元素前面的元素映射的连续值，已经被count保存了起来，只要后面来的元素大于num，那么一定大于 num大于的元素

class StockSpanner {
public:
    StockSpanner() {}
    
    int next(int price) {
 
         int sum=1;
        while(!val.empty()&&price>=val.top())
        {
            sum+=count.top();
            count.pop();
            val.pop();
        }
            
        val.push(price);
        count.push(sum);
        
        return count.top();
    }
    stack<int> val;
    stack<int> count; 
};

买卖股票的最佳时机含手续费

给定一个整数数组 prices，其中第 i 个元素代表了第 i 天的股票价格 ；非负整数 fee 代表了交易股票的手续费用。你可以无限次地完成交易，但是你每笔交易都需要付手续费。如果你已经购买了一个股票，在卖出它之前你就不能再继续购买股票了。返回获得利润的最大值。注意：这里的一笔交易指买入持有并卖出股票的整个过程，每笔交易你只需要为支付一次手续费。

题解：

设dp[i][n]表示第i天结束时的状态，此时状态有两种 dp [i][0]表示当天结束手里头有股票的利润，dp[i][1]表示当天结束，手里头没有股票的利润

令dp[0][0]=-prices[0] 表示第一天买入股票时，利润为负数

转移方程推导：

1.dp[i][0]表示第i天时，手里面有股票的利润，第i天手里面有股票，那么这个股票可以是上一天的，可以是今天买入的

继承昨天的股票：dp[i][0]=dp[i-1][0] 。
今天新买入股票，则说明昨天手里是没有股票的 dp[i][0] = dp[i-1][1] - prices[i]
-> dp[i][0]=fmax(dp[i-1][0],dp[i-1][1]-prices[i])

2.dp[i][1]，表示第i天没有股票时，手里头的利润，那么这个状态可以是上一天就没有股票，也可以是上一天有股票今天卖了

上一天没有股票：dp[i][1]=dp[i-1][1]
上一天有股票今天卖了：dp[i][1]=dp[i-1][0]+prices[i]-fee
-> dp[i][1]=fmax(dp[i-1][1],dp[i-1][0]+prices[i]-fee)

3.最终的最大利润为最后一天时，手里头没有股票时的利润

class Solution {
public:
    int maxProfit(vector<int>& prices, int fee) {
        //每进行一次买入卖出，需要交一笔手续费
        //dp[i][n]表示当天结束时的状态
        //此时有两种状态
        //dp[i][0] 表示手里有股票
        //dp[i][1] 表示手里没有股票

        vector<vector<int>>dp(prices.size(),vector<int>(2,0));
        if(prices.size()==0)
            return 0;

        dp[0][0]=-prices[0];//第一天买入股票

        for(int i=1;i<prices.size();i++)//从第二天开始
        {
            dp[i][0]=fmax(dp[i-1][0],dp[i-1][1]-prices[i]);//上一天，或者今天买入的
            dp[i][1]=fmax(dp[i-1][1],dp[i-1][0]+prices[i]-fee);//今天卖出去了，或者本来就没有
        }

        return fmax(dp[prices.size()-1][0],dp[prices.size()-1][1]) ;
    }
};

最佳买卖股票时机含冷冻期

给定一个整数数组，其中第 i 个元素代表了第 i 天的股票价格 。设计一个算法计算出最大利润。在满足以下约束条件下，你可以尽可能地完成更多的交易（多次买卖一支股票）:你不能同时参与多笔交易（你必须在再次购买前出售掉之前的股票）。卖出股票后，你无法在第二天买入股票 (即冷冻期为 1 天)。

题解：

dp[i][n]表示在第i天结束时的状态，n此时有三种状态 ，dp[i][0]=持有股票 dp[i][1]=处于冷冻期 dp[i][2]=不处于冷冻期，且不持有股票

转移方程推导：

1.dp[i][0]表示第i天时，手里面持有股票， 那么这个股票可以是上一天的，或者是今天买入的，今天买入，则上一天不能处于冷冻期
dp[i][0]=max(dp[i-1][0],dp[i-1][2] - prices[i])

2.dp[i][1]表示第i天时，处于冷冻期，那么今天卖出了股票，则上一天必须是有股票的
dp[i][1] =prices[i] + dp[i-1][0]

3.dp[i][2]表示第i天时，即不处于冷冻期，也不持有股票，那么这个状态可以是上一天的延续，也可以是上一天处于冷冻期
dp[i][2] = max(dp[i-1][1],dp[i-2][2])

class Solution {
public:
    int maxProfit(vector<int>& prices) {
        //dp[i][n]表示在第i天结束时的状态
        //其中 n有三种状态 
        //dp[i][0]=持有股票  dp[i][1]=处于冷冻期  dp[i][2]=不处于冷冻期，且不持有股票

        //第n天的状态只于第n-1天有关系

        //dp[i][0]=max(dp[i-1][0],dp[i-1][2] - prices[i])//前一天就有股票，或者今天买的

        //dp[i][1] =prices[i] + dp[i-1][0] //在当天卖出了股票,昨天就是有股票的 + 当天的股票价格

        //dp[i][2] = max(dp[i-1][1],dp[i-2][2])//当天没有进行任何操作,前一天没有股票或者前一天处于冷冻期

        if(prices.empty())
            return 0;

       vector<vector<int>>dp(prices.size(),vector<int>(3,0));

        //dp[0][1]=0 第一天不可能处于冷冻期  dp[0][2]=0第一天不进行任何操作
        dp[0][0]=-prices[0];//第一天买入股票，收入为负数
        
        for(int i=1;i<prices.size();i++)//从二天开始
        {
            dp[i][0]=fmax(dp[i-1][0],dp[i-1][2] - prices[i]);
            dp[i][1] =prices[i] + dp[i-1][0];
            dp[i][2] = fmax(dp[i-1][1],dp[i-1][2]);
        }

        return fmax(dp[prices.size()-1][0],fmax(dp[prices.size()-1][1],dp[prices.size()-1][2]));
    }
};

买卖股票的最佳时机III

给定一个数组，它的第 i 个元素是一支给定的股票在第 i 天的价格。设计一个算法来计算你所能获取的最大利润。你最多可以完成 两笔 交易。注意：你不能同时参与多笔交易（你必须在再次购买前出售掉之前的股票）

题解：

1.状态设定：

一天结束时，有4种如下状态：
buy1：进行第一次买入； sell1：进行第一次售出； buy2：进行第二次买入；sell2：进行第二次售出

2.状态分析：

buy1:每次买入都应该挑最小的进行买入 -> buy1=fmax(buy1,-prices[i])
sell1:每次卖出，都应该挑选最高的价格进行卖出 -> sell1=famx(sell1,buy1+prices[i])

buy2:在卖第二次的时候，第一次的股票必须是出售的状态,因此利润为第一次卖出时的利润减去买入股票的价格 -> buy2=famx(buy2,sell1-prices[i])

sell2:在价格较高时，进行卖出 -> sell2 = fmax(sell2,prices[i])

class Solution {
public:
    int maxProfit(vector<int>& prices) {
        //两种状态，手持股票，或者不持
        //最多完成两笔交易
        
        int buy1=-prices[0];//第一次买入
        int buy2=-prices[0];//第二次买入
        int sell1=0;//第一次卖出
        int sell2=0;//第二次卖出

        for(int i=1;i<prices.size();i++)
        {
            buy1=fmax(buy1,-prices[i]);//挑选最小的值进行一次买入
            sell1=fmax(sell1,buy1+prices[i]);//挑选一次最大的值，进行第一次卖出
            
            buy2=fmax(buy2,sell1-prices[i]);//买第二次时的利润=第一次的利润-当前股票价格
            sell2=fmax(sell2,buy2+prices[i]);//挑选一个较大的值，进行第二次卖出
        }

        return sell2;
    }
};

买卖股票的最佳时机IV

给定一个整数数组 prices ，它的第 i 个元素 prices[i] 是一支给定的股票在第 i 天的价格。设计一个算法来计算你所能获取的最大利润。你最多可以完成 k 笔交易。注意：你不能同时参与多笔交易（你必须在再次购买前出售掉之前的股票）

题解：

本题和上题其实是一样的，只是在给定变量的时候不是给定2组，而是给定K组

class Solution {
public:
    int maxProfit(int k, vector<int>& prices) {
        if(prices.size()==0||k==0)
            return 0;
        vector<int> buy(k,-prices[0]);
        vector<int> sell(k,0);

        for(int i=1;i<prices.size();i++)
        {
            for(int j=0;j<k;j++)
            {
                if(j==0)//第一次
                {
                    buy[j]=fmax(buy[j],-prices[i]);
                    sell[j]=fmax(sell[j],buy[j]+prices[i]);
                }
                else//非第一次
                {
                    buy[j]=fmax(buy[j],sell[j-1]-prices[i]);//上一次卖出去的利润 - 当前买股价格
                    sell[j]=fmax(sell[j],buy[j]+prices[i]);//判断是否卖出去
                }
            }
        }

        return sell[k-1];
    }
};