TSP问题模拟退火算法求解TSP问题matlab源码

Posted 2021-06-24 MatlabQQ1575304183

二、 模拟退火算法

1. 算法
模拟退火算法可分为解空间、目标函数和初始解三部分，其基本思想是：
（1）初始化：初始温度T(充分大)，初始解状态s(是算法迭代的起点)，每个T值的迭代次数L；
（2）对k=1，……，L做第(3)至第6步；
（3）产生新解s′；
（4）计算增量cost=cost(s′)-cost(s)，其中cost(s)为评价函数；
（5）若t<0则接受s′作为新的当前解，否则以概率exp(-t′/T)接受s′作为新的当前解；
（6）如果满足终止条件则输出当前解作为最优解，结束程序。终止条件通常取为连续若干个新解都没有被接受时终止算法；
（7）T逐渐减少，且T趋于0，然后转第2步运算。

2. 参数选择
（1）温度T的初始值设置。
温度T的初始值设置是影响模拟退火算法全局搜索性能的重要因素之一。初始温度高，则搜索到全局最优解的可能性大，但因此要花费大量的计算时间；反之，则可节约计算时间，但全局搜索性能可能受到影响。实际应用过程中，初始温度一般需要依据实验结果进行若干次调整。
（2）温度衰减函数的选取。
衰减函数用于控制温度的退火速度，一个常用的函数为：
T(t+1)=aT(t)
式中a是一个非常接近于1的常数，t为降温的次数。
（3）马尔可夫链长度L的选取。
通常的原则是：在衰减参数T的衰减函数已选定的前提下，L的选取应遵循在控制参数的每一取值上都能恢复准平衡的原则。

三、TSP算法实现

1. TSP算法描述
（1）TSP问题的解空间和初始解
TSP的解空间S是遍访每个城市恰好一次的所有回路，是所有城市排列的集合。TSP问题的解空间S可表示为{1,2,…,n}的所有排列的集合，即S = {(c1,c2,…,cn) | ((c1,c2,…,cn)为{1,2,…,n}的排列）}，其中每一个排列Si表示遍访n个城市的一个路径，ci= j表示在第i次访问城市j。模拟退火算法的最优解与初始状态无关，故初始解为随机函数生成一个{1,2,…,n}的随机排列作为S0。
（2）目标函数
TSP问题的目标函数即为访问所有城市的路径总长度，也可称为代价函数：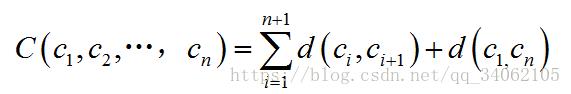

现在TSP问题的求解就是通过模拟退火算法求出目标函数C(c1,c2,…,cn)的最小值，相应地，s*= (c*1,c*2,…,c*n)即为TSP问题的最优解。
（3）新解产生
新解的产生对问题的求解非常重要。新解可通过分别或者交替用以下2种方法产生：
①二变换法：任选序号u,v(设uvn)，交换u和v之间的访问顺序，若交换前的解为si= (c1,c2,…,cu,…,cv,…,cn),交换后的路径为新路径，即：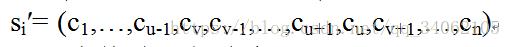

②三变换法：任选序号u,v和ω(u≤vω)，将u和v之间的路径插到ω之后访问，若交换前的解为si= (c1,c2,…,cu,…,cv,…,cω,…,cn)，交换后的路径为的新路径为：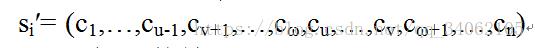

（4）目标函数差
计算变换前的解和变换后目标函数的差值：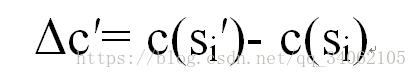

（5）Metropolis接受准则
根据目标函数的差值和概率exp(-ΔC′/T)接受si′作为新的当前解si，接受准则：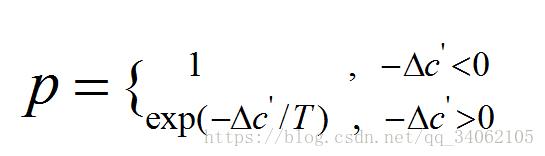

2 TSP算法流程
根据以上对TSP的算法描述，可以写出用模拟退火算法解TSP问题的流程图2 所示：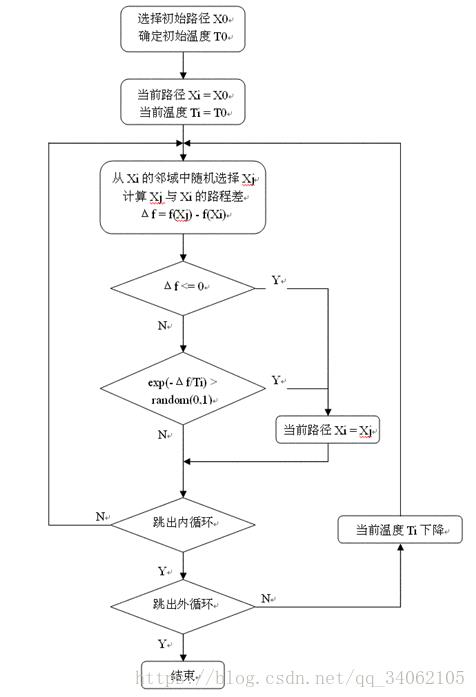

 clc;
clear;
close all;
%%
tic
T0=1000;   % 初始温度
Tend=1e-3;  % 终止温度
L=200;    % 各温度下的迭代次数（链长）
q=0.9;    %降温速率
% X=[16.4700   96.1000
%    16.4700   94.4400
%    20.0900   92.5400
%    22.3900   93.3700
%    25.2300   97.2400
%    22.0000   96.0500
%    20.4700   97.0200
%    17.2000   96.2900
%    16.3000   97.3800
%    14.0500   98.1200
%    16.5300   97.3800
%    21.5200   95.5900
%    19.4100   97.1300
%    20.0900   92.5500];
data=load('eil51.txt');
cityCoor=[data(:,1) data(:,2)];%城市坐标矩阵
%%
% D=Distanse(X);  %计算距离矩阵
 D=Distanse(cityCoor);  
N=size(D,1);    %城市的个数
%% 初始解
S1=randperm(N);  %随机产生一个初始路线

%% 画出随机解的路径图
% DrawPath(S1,X)
DrawPath(S1,cityCoor)
pause(0.0001)
%% 输出随机解的路径和总距离
disp('初始种群中的一个随机值:')
OutputPath(S1);
Rlength=PathLength(D,S1);
disp(['总距离：',num2str(Rlength)]);

%% 计算迭代的次数Time
Time=ceil(double(solve(['1000*(0.9)^x=',num2str(Tend)])));
count=0;        %迭代计数
Obj=zeros(Time,1);         %目标值矩阵初始化
track=zeros(Time,N);       %每代的最优路线矩阵初始化
%% 迭代
while T0>Tend
    count=count+1;     %更新迭代次数
    temp=zeros(L,N+1);
    for k=1:L
        %% 产生新解
        S2=NewAnswer(S1);
        %% Metropolis法则判断是否接受新解
        [S1,R]=Metropolis(S1,S2,D,T0);  %Metropolis 抽样算法
        temp(k,:)=[S1 R];          %记录下一路线的及其路程
    end
    %% 记录每次迭代过程的最优路线
    [d0,index]=min(temp(:,end)); %找出当前温度下最优路线
    if count==1 || d0<Obj(count-1)
        Obj(count)=d0;           %如果当前温度下最优路程小于上一路程则记录当前路程
    else
        Obj(count)=Obj(count-1);%如果当前温度下最优路程大于上一路程则记录上一路程
    end
    track(count,:)=temp(index,1:end-1);  %记录当前温度的最优路线
    T0=q*T0;     %降温
    fprintf(1,'%d\\n',count)  %输出当前迭代次数
end
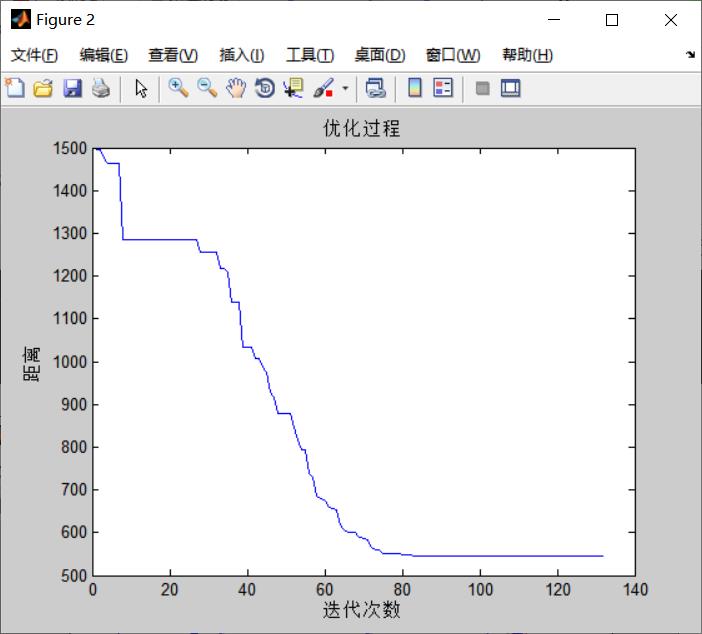
%% 优化过程迭代图
figure
plot(1:count,Obj)
xlabel('迭代次数')
ylabel('距离')
title('优化过程')

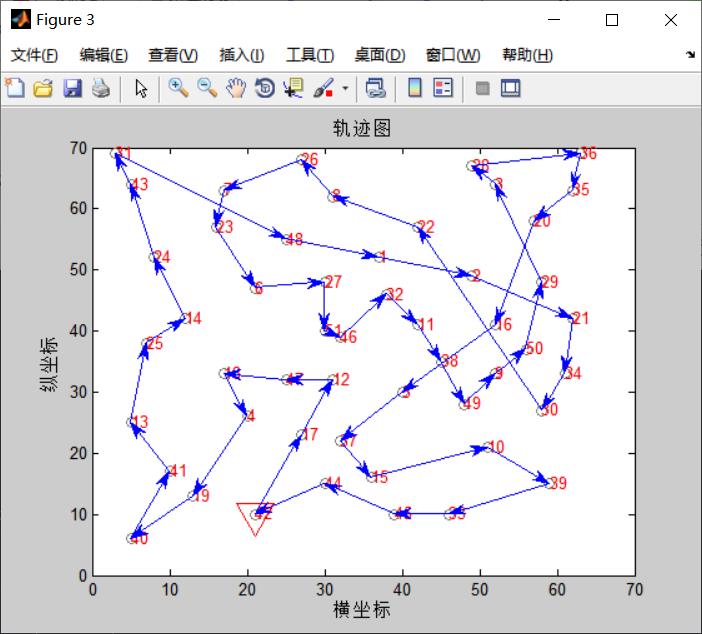
%% 最优解的路径图
DrawPath(track(end,:),cityCoor)

%% 输出最优解的路线和总距离
disp('最优解:')
S=track(end,:);
p=OutputPath(S);
disp(['总距离：',num2str(PathLength(D,S))]);
disp('-------------------------------------------------------------')
toc

​

完整代码添加QQ1575304183