路径规划基于蚁群算法求解最短路径matlab

Posted 2021-06-24 MatlabQQ1575304183

   

一、蚁群算法的基本原理

1、蚂蚁在路径上释放信息素。

2、碰到还没走过的路口，就随机挑选一条路走。同时，释放与路径长度有关的信息素。

3、信息素浓度与路径长度成反比。后来的蚂蚁再次碰到该路口时，就选择信息素浓度较高路径。

4、最优路径上的信息素浓度越来越大。

5、最终蚁群找到最优寻食路径。

 

 

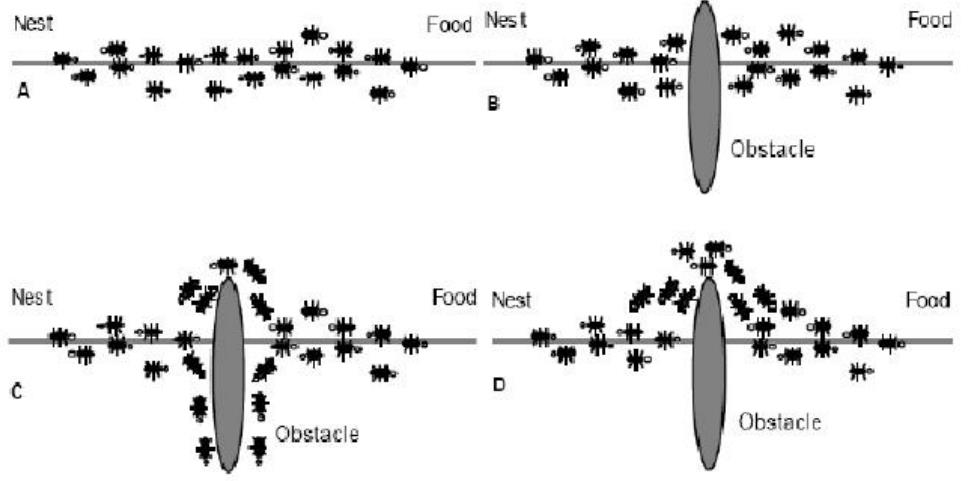
 蚁群走过较短的那一侧的蚂蚁数数量会多于较长那一侧的，所以留下的信息素就会多，渐渐的蚂蚁就只走较短的那一侧了。

 

蚁群算法对TSP的求解主要有两大步骤：（TSP问题就是要找到最短哈密尔顿回路）

1、路径构建

AS中的随机比例规则；对于每只蚂蚁k，路径记忆向量R^k.按照访问顺序记录了所有k已经经过的城市序号。设蚂蚁k当前所在城市为i,则其选择城市j作为下一个访问对象的概率为:

 

 

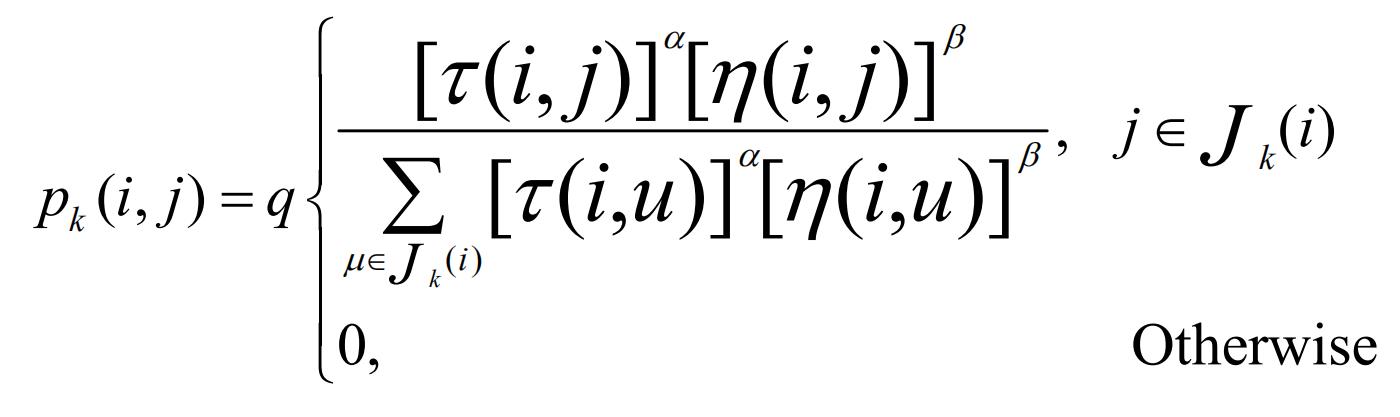
2、信息素更新

 

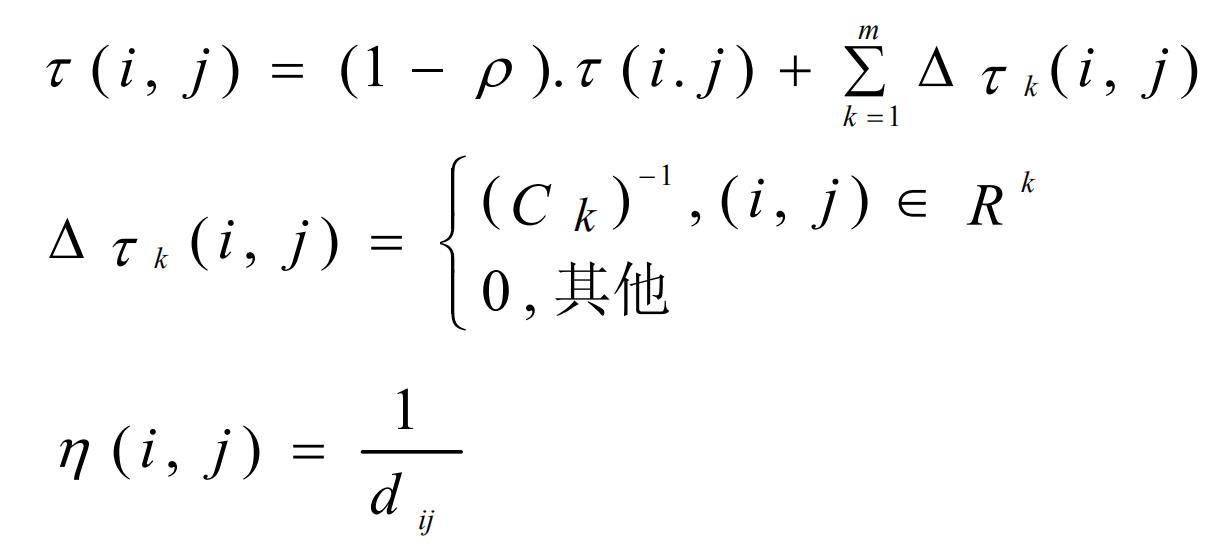
这里m是蚂蚁个数, ρ是信息素的蒸发率，规定0≤ ρ≤1，在AS中通常设置为 ρ =0.5，Δτij是第k只蚂蚁在它经过的边上释放的信息素量，它等于蚂蚁k本轮构建路径长度的倒数。C^k表示路径长度，它是R^k中所有边的长度和。

构建图：构建图与问题描述图是一致的，成份的集合C对应着点的集合（即：C=N），连接对应着边的集合（即L=A）,且每一条边都带有一个权值，代表点i和j之间的距离。

约束条件：所有城市都要被访问且每个城市最多只能被访问一次。

信息素和启发式信息：TSP 问题中的信息素表示在访问城市i后直接访问城市j的期望度。启发式信息值一般与城市i和城市j的距离成反比。

解的构建：每只蚂蚁最初都从随机选择出来的城市出发，每经过一次迭代蚂蚁就向解中添加一个还没有访问过的城市。当所有城市都被蚂蚁访问过之后，解的构建就终止。

 

 

 

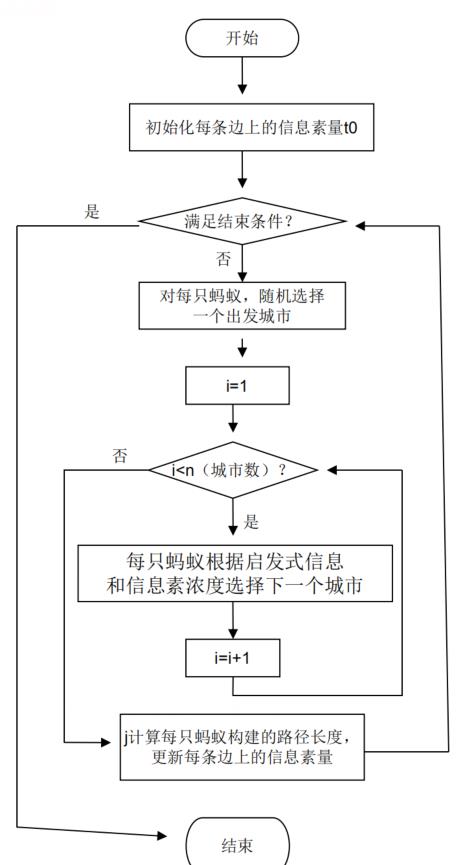
蚁群算法存在缺陷：

蚁群算法在解决小规模TSP问题是勉强能用，稍加时间就能发现最优解，但是若问题规模很大，蚁群算法的性能会极低，甚至卡死。所以可以进行改进，例如精英蚂蚁系统。

精英蚂蚁系统是对基础蚁群算法的一次改进，它在原AS信息素更新原则的基础上增加了一个对至今最优路径的强化手段。在每轮信息素更新完毕后，搜索到至今最优路径的那只蚂蚁将会为这条路径添加额外的信息素。精英蚂蚁系统引入 这种额外的信息素强化手段有助于更好的引导蚂蚁搜索的偏向，使算法更快收敛

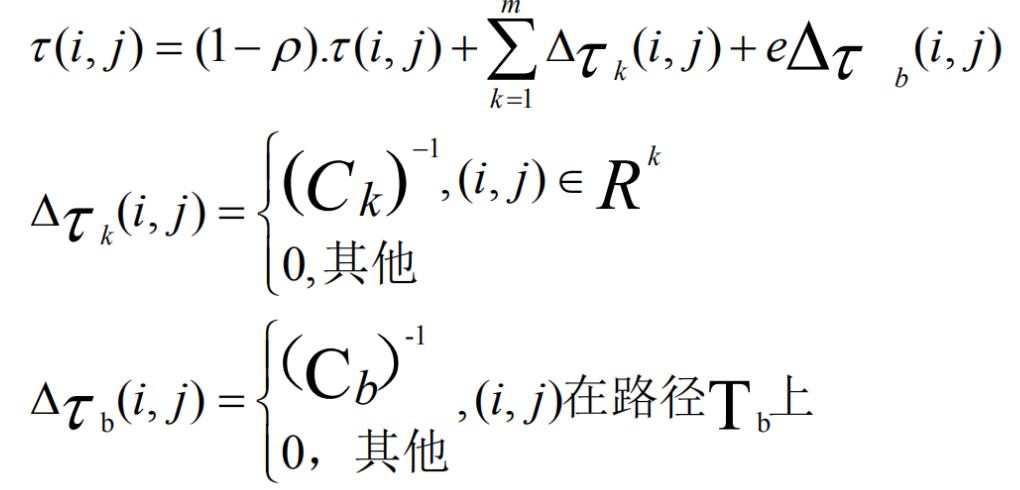
二、代码

% Ant main program

clear all;
close all;
clc;

tic;
Ant=25;%蚂蚁数量
Ger=120;%迭代次数
first_address = [
    100,10
    150,10
    180,30
    200,10
    200,200
    200,220
    180,240
    180,270
    150,270
    100,240
    80,240
    50,270
    200,300
    10,300
    10,270
    10,240
    10,200
    10,10
    50,30
    100,10
    ];%first_address表示测试数据中的节点坐标

SumOfCity = size(first_address,1);%节点个数
length_address =10000.*ones(SumOfCity,SumOfCity);%length_address表示两两节点间的距离，初始设定10000，可以设定无穷大，表示不相连
length_address(1,2)=377;%表示节点1和节点2的距离
length_address(2,4)=190;
length_address(2,3)=100;
length_address(3,4)=101;
length_address(4,5)=240;
length_address(5,17)=1932;
length_address(5,6)=70;
length_address(6,13)=200;
length_address(6,7)=63.1;

length_address(7,10)=377;
length_address(7,8)=87.5;
length_address(8,9)=100;
length_address(10,11)=8;
length_address(9,10)=170.8;
length_address(9,12)=332.9;
length_address(11,12)=168.8;
length_address(11,16)=375.2;
length_address(12,15)=135.1;

length_address(13,14)=458;
length_address(14,15)=100;
length_address(15,16)=86.7;
length_address(16,17)=187.5;
length_address(17,18)=639.8;

length_address(18,20)=510.5;
length_address(18,19)=200.1;
length_address(19,20)=246.8;
for   n=1:size(first_address)
    for m=1:size(first_address)
        if length_address(n,m)~=10000
            length_address(m,n)=length_address(n,m);   %对称矩阵
        end
    end
end

power=length_address;%距离
[PM PN]=size(power);%距离矩阵大小，行列个数
% %% 画出节点分布图形
% figure(1);
% grid on;
% hold on;
% scatter(first_address(:,1),first_address(:,2));
% for i=1:PN
%     for j=1:PN
%         if(length_address(i,j)~=10000)
%             line([first_address(i,1),first_address(j,1)],[first_address(i,2),first_address(j,2)],'Color','g');%划线
%             text((first_address(i,1)+first_address(j,1))/2,(first_address(i,2)+first_address(j,2))/2,num2str(length_address(i,j)));%标注线段距离
%         end
%     end
% end



% 初始化蚂蚁位置
v=init_population(Ant,PN);
v(:,1)=1;%起点
v(:,PN)=1;%终点

fit=short_road_fun(v,power);%求每条路径的距离
T0 = max(fit)-fit;


% 初始化
vmfit=[];
vx=[];
P0=0.2;           % P0----全局转移选择因子
P=0.8;            % P ----信息素蒸发系数
%C=[];
% 开始寻优
for i_ger=1:Ger
    lamda=1/i_ger;    % 转移步长参数
    [T_Best(i_ger),BestIndex]=max(T0);
    for j_g=1:Ant    % 求取全局转移概率
        r=T0(BestIndex)-T0(j_g);
        Prob(i_ger,j_g)=r/T0(BestIndex);
    end
    %对100只蚂蚁进行路径的转变
    for j_g_tr=1:Ant
        %路径进行改变，该路径存放到temp变量，1表示经过该列所在的节点数
        if Prob(i_ger,j_g_tr)<P0
            M=rand(1,PN)<lamda;
            temp=v(j_g_tr,:)-2.*(v(j_g_tr,:).*M)+M;
        else
            M=rand(1,PN)<P0;
            temp=v(j_g_tr,:)-2.*(v(j_g_tr,:).*M)+M;
        end
        temp(:,1)=1;%起点和终点必须有蚂蚁存在
        temp(:,end)=1;
        %判转变后的临时路径距离是否小于原来的路径，是的话就将该蚂蚁的路径进行转换成temp中存放的路径
        if short_road_fun(temp,power)<short_road_fun(v(j_g_tr,:),power)
            v(j_g_tr,:)=temp;
        end
    end
    
    %信息素更新
    
       [sol,indb]=min(fit);
    v(1,:)=v(indb,:);%第一只蚂蚁的路径保存最小路径
    media=mean(fit);
    vx=[vx sol];%存放每一代最小的距离
    %     vmfit=[vmfit media];
    
    
end

% % % % % % % % % % % % % % % % % % % % % % % % % % % % % % % % %
%%%% 最后结果
% 显示最优解及最优值
% v(indb,:)
disp(sprintf('Code of shortroad is: %s',num2str(v(indb,:))));
disp(sprintf('\\n'));    %空一行
disp(sprintf('Shortroad is: %s',num2str(find(v(indb,:)))));
disp(sprintf('Mininum is: %d',sol));
route=find(v(indb,:));
% 画出节点分布图形
figure(2);
grid on;
hold on;
for i=1:PN-1
    plot(first_address(i,1),first_address(i,2),'bo','MarkerSize',10);
    str=num2str(i);
    text(first_address(i,1)-10,first_address(i,2)+10,str,'Color','red','FontSize',15);
end
m=length(route);
for i=1:m
    plot(first_address(route(i),1),first_address(route(i),2),'MarkerSize',10,'MarkerEdgeColor','k','MarkerFaceColor',[0.5,0.5,0.5])  ;
    hold on;
end
for i=1:PN
    for j=1:PN
        if(length_address(i,j)~=10000)
            line([first_address(i,1),first_address(j,1)],[first_address(i,2),first_address(j,2)],'Color','g','LineWidth',5);%划线
            text((first_address(i,1)+first_address(j,1))/2,(first_address(i,2)+first_address(j,2))/2,num2str(length_address(i,j)));%标注线段距离
        end
    end
end
%% 最短路径
for p=1:m-1
    if(route(p+1)~=20)
        line([first_address(route(p),1),first_address(route(p+1),1)],[first_address(route(p),2),first_address(route(p+1),2)],'Color','r','LineWidth',5);%划线
        text((first_address(route(p),1)+first_address(route(p+1),1))/2,(first_address(route(p),2)+first_address(route(p+1),2))/2,num2str(length_address(route(p),route(p+1))));%标注线段距离
    else
        line([first_address(route(p),1),first_address(1,1)],[first_address(route(p),2),first_address(1,2)],'Color','r','LineWidth',5);%划线
        text((first_address(route(p),1)+first_address(1,1))/2,(first_address(route(p),2)+first_address(1,2))/2,num2str(length_address(route(p),route(p+1))));%标注线段距离
    end
end
axis([0 250 0 400])
% 图形显示最优及平均函数值变化趋势
% figure(3);
% plot(vx);
% title('最优,平均函数值变化趋势');
% xlabel('Generations');
% ylabel('f(x)');
% hold on;
% plot(vmfit,'r');
% hold off;

runtime=toc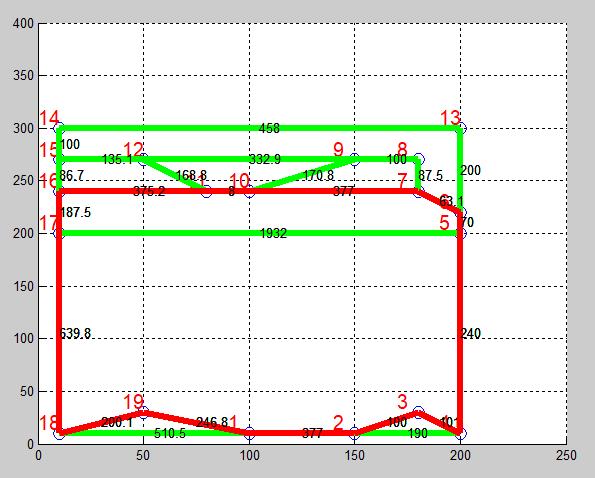

​

完整代码添加QQ1575304183