降维算法PCA的应用----高维数据的可视化

Posted 2021-06-24 iostreamzl

文章目录

• • 序言
  • 废话不多说看代码
  • • 导入相关模块
    • 数据提取
    • 降维
    • • 降维后数据信息展示
      • 新的特征矩阵
    • 可视化
    • • 关于X_dim2[y==i, 0]的解释
  • 总结

序言

当我们拿到一堆数据的时候，几乎不可能通过我们的肉眼分辨出数据的分布情况，这时候就想要通过图展示数据的分布，但是现实中数据往往维度很高，而我们人类能看到的最高维度就三维，这时我们就可以通过降维算法PCA将维度降低到三位之下，便于我们观察数据的分布。注意点这里讲的方式只适用于分类型标签数据的可视化

废话不多说看代码

本次使用的数据是sklearn自带的鸢尾花数据集

导入相关模块

from sklearn.datasets import load_iris
from sklearn.decomposition import PCA
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt

%matplotlib inline

数据提取

# 提取特征和标签
iris = load_iris()
X = iris['data']
y = iris['target']

降维

# 实例化PCA，并实现数据降维
pca_2 = PCA(n_components=2)
X_dim2 = pca_2.fit_transform(X)

降维后数据信息展示

# 通过explained_variance_s属性查看降维后的每个特征的可解释性方差的大小
# 方差越大带有的有效信息越大
pca_2.explained_variance_
# array([4.22824171, 0.24267075])

# 通过explained_variance_ratio_属性查看降维后的每个特征所占信息量占原始信息量的比例
pca_2.explained_variance_ratio_
# array([0.92461872, 0.05306648])

# 查看降维后的所有特征信息量占原始数据的比例
pca_2.explained_variance_ratio_.sum()
# 0.9776852063187949

97%的展现率，可以说画出来的图基本接近原始数据的分布的

新的特征矩阵

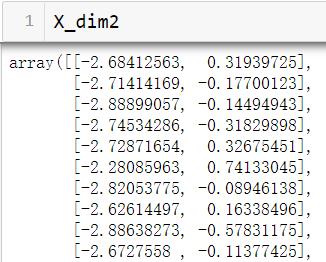
可视化

# 可视化
# 将第一个特征作为x，第二个特征作为y

color = ['red', 'green', 'blue']

# 取出标签中的所有类别
label = np.unique(y) # [0, 1, 2]

for i in label :
	# 这里采用的是bool索引
    x = X_dim2[y==i, 0]
    y1 = X_dim2[y==i, 1]
    plt.scatter(x, y1, c=color[i])

plt.show()

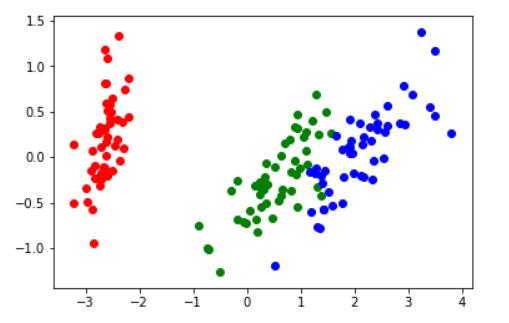
这就是大名鼎鼎的鸢尾花数据集的分布了。可能有一点点的误差，毕竟新的特征举证只能表现原数据97%的信息。但是数据大致的分布情况是没错的

关于X_dim2[y==i, 0]的解释

这里能这么做的原因在于。我没有对我的数据进行行方向上的变化，也就是说没有交换过行的位置。
那么最终的数据与标签y依然是一一对应的关系。通过这个索引获得的数据，依然符合原数据的分布。

# 以y == 0 为例
y == 0
'''
array([ True,  True,  True,  True,  True,  True,  True,  True,  True,
        True,  True,  True,  True,  True,  True,  True,  True,  True,
        True,  True,  True,  True,  True,  True,  True,  True,  True,
        True,  True,  True,  True,  True,  True,  True,  True,  True,
        True,  True,  True,  True,  True,  True,  True,  True,  True,
        True,  True,  True,  True,  True, False, False, False, False,
       False, False, False, False, False, False, False, False, False,
       False, False, False, False, False, False, False, False, False,
       False, False, False, False, False, False, False, False, False,
'''
# 遍历y，只要遇到为0的情况，相应位置则为true。
# 最终返回一个bool矩阵
X_dim2[y==0, 0]
# 通过y==0返回的bool索引，取出为true对应的行，在取第一列

总结

降维算法PCA的真的很强大。当不知道数据分布的情况下，大可以通过降维画出数据分布，然后再选择比较适合的模型来进行数据的预测。

---

欢迎在评论区和我共同讨论