密码学——公钥密码体系之RSA算法2
Posted 摆渡沧桑
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了密码学——公钥密码体系之RSA算法2相关的知识,希望对你有一定的参考价值。
密码学——公钥密码体系之RSA算法2
一、RSA算法背景
上一讲介绍了公钥密码体系中的背包算法,在Merkle背包算法出现后不久,便出现了第一个比较完善的公开秘钥算法RSA,它可以用于加密也可以用于数字签名(一般常用作数字签名,速度较快)。
RSA算法以它的三个发明者Ron Rivest,Adi Shamir和Leonard Adleman的名字命名。
RSA的安全基于大数分解的难度。其公开密钥和私人秘钥是一对大素数的函数。从一个公开密钥和密文中恢复出明文的难度等价于分解两个大素数之积。
二、RSA算法描述
- 为了产生两个密钥,选取两个大素数
p
p
p和
q
q
q.为了获得最大程度的安全性,两数的长度一样。计算乘积。
n = p q n=pq n=pq - 然后随机算去加密密钥
e
e
e,使得
e
e
e 和
(
p
−
1
)
(
q
−
1
)
(p-1)(q-1)
(p−1)(q−1)互素。最后用欧几里得扩展算法计算解密密钥
d
d
d,以满足
e d = 1 m o d ( p − 1 ) ( q − 1 ) ed = 1 mod (p-1)(q-1) ed=1mod(p−1)(q−1)
则
d = e − 1 m o d ( p − 1 ) ( q − 1 ) d=e^{-1}mod(p-1)(q-1) d=e−1mod(p−1)(q−1)
其中, d d d与 n n n也互素。 e e e和 n n n是公开密钥,两个素数 p p p和 q q q不再需要,他们应该被舍弃,但绝不能泄露
加密消息
m
m
m时,首先将它分成比n小的数据分组(采用二进制数,选取小于n的2的最大次幂)。也就是说,如果
p
p
p和
q
q
q为100位素数,那么n将有200位,每个消息分组mi应小于200位长(如果需要加密固定的消息分组,那么可以在它的左边填充0,并确保该数比n小)。加密后的密文c,将由相同长度的分组ci组成。加密公式简化为:
c
i
=
m
i
e
m
o
d
(
n
)
c_i=m_i^emod(n)
ci=miemod(n)
解密消息时,取每一个加密后的分组ci并计算:
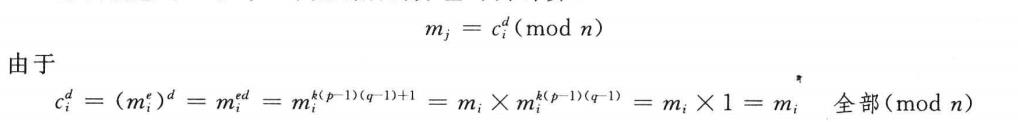
这个公式能恢复明文,如下

消息用d加密就像用e解密一样容易。
举一个简单的例子:
选择
p
=
47
p=47
p=47,
q
=
71
q=71
q=71,那么
n
=
p
q
=
3347
n=pq=3347
n=pq=3347
加密密钥
e
e
e必须与
(
p
−
1
)
(
q
−
1
)
=
46
∗
70
=
3220
(p-1)(q-1)=46*70=3220
(p−1)(q−1)=46∗70=3220没有公因子。
随机选取
e
=
79
e=79
e=79,那么:
d
=
7
9
−
1
m
o
d
3220
=
1019
d=79^{-1}mod3220=1019
d=79−1mod3220=1019
该结果使用扩展欧几里得算法求出。公开
e
e
e和
n
n
n,将
d
d
d保密,丢弃
p
p
p和
q
q
q。
对于加密消息:
m
=
688232687966668003
m=688232687966668003
m=688232687966668003
首先将其分为小的分组。在此例中,按3位数字一组就可以进行加密。这个消息将分成6个分组m,进行加密:
m
1
=
688
m_1=688
m1=688
m
2
=
232
m_2=232
m2=232
m
3
=
687
m_3=687
m3=687
m
4
=
966
m_4=966
m4=966
m
5
=
668
m_5=668
m5=668
m
6
=
003
m_6=003
m6=003
第一个分组加密为:
68
8
79
m
o
d
3337
=
1570
=
c
1
688^{79}mod3337 = 1570 = c_1
68879mod3337=1570=c1
对随后的分组进行同样的运算产生加密后的密文:
c
=
15702756209122762423158
c=15702756209122762423158
c=15702756209122762423158
解密消息时需要用解密密钥1019进行相同的指数运算。因而
157
0
1019
m
o
d
3337
=
688
=
m
1
1570^{1019}mod3337=688=m_1
15701019mod3337=688=m1
消息的其余部分可用同样的方法恢复出来
三、RSA的硬件实现
-
已有的RSA芯片
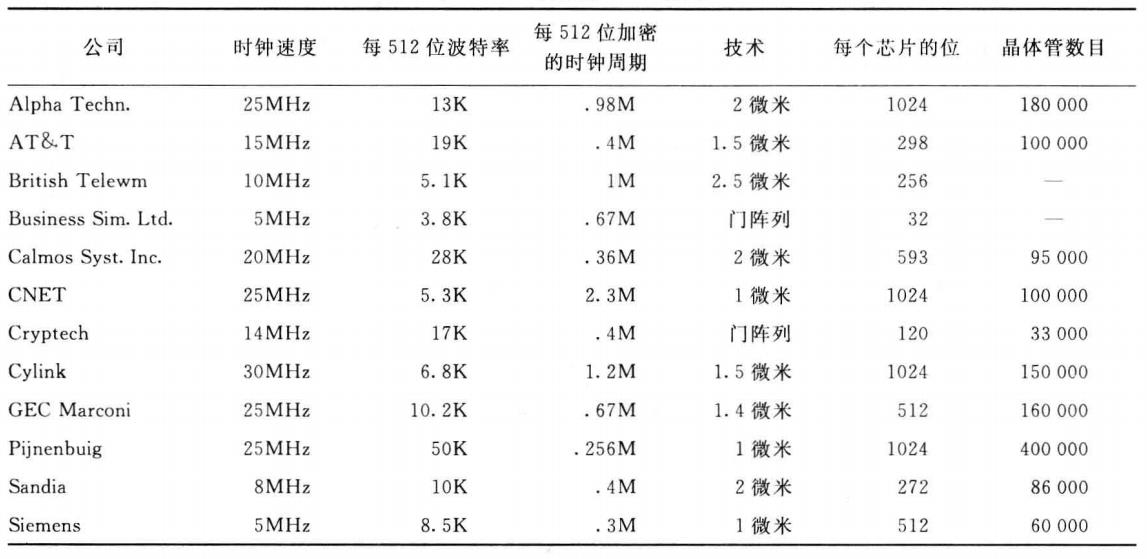
-
RSA速度
RSA硬件实现时,RSA比DES慢大约1000倍。最快的具有512位模数的VLSI硬件实现的吞吐量为64Kbit每秒。也有一些实现1024位RSA的加密芯片。如今设计512bit的芯片可以达到1Mb/s,该芯片在1995年制成。在智能卡中已经大量实现了RSA,这些实现都比较慢。有兴趣的读者可以关注我之前的专门RSA硬件设计专栏:
基于Montgomery算法的高速、可配置RSA密码IP核硬件设计系列博文软件实现时,DES大约比RSA快100倍。这些数字会随着技术发展而发生相应的变化,但RSA的速度将永远不会达到对称算法的速度。下表给出了软件实现RSA算法的情况:

-
RSA硬件和软件加速
对于RSA硬件实现,可以采用蒙哥马利算法来加速硬件。如果很适当的选择了一个 e e e值,RSA加密速度将快很多。最常用的三个 e e e值为3,17和65537(2^16+1)(二进制表示只有两个1,所以只需要17次乘法来实现指数运算)。
X.509中建议采用65537;
PEM中建议采用3;
PKCS#1中建议采用3和65537;即便是一组用户使用同样的 e e e值,采用这三个值中的任何一个都不存在安全问题
假如已经保存了 p p p和 g g g值,以及诸如 d m o d ( p − 1 ) 、 q − 1 d m o d ( p − 1 ) 、 m o d p dmod(p-1)、q^{-1}dmod(p-1)、modp dmod(p−1)、q−1dmod(p−1)、modp这类数,那么运用中国剩余定理就能使私人密钥的运行速度加快。这些数很容易从私人密钥和公开密钥中计算出来。
四、RSA的安全性
对于RSA的安全性完全依赖于大数分解的难度,从技术上来说,这是不正确的,只是一种推测。
从数学上从未证明过,需要分解n才能从
e
e
e和
c
c
c中计算出
m
m
m。用一种完全不同方法来对RSA进行密码分析还只是一种想象。如果这种新方法能让密码分析者推算出
d
d
d,也可以作为分解大数的一种新方法。
也可以通过猜测 ( p − 1 ) ( q − 1 ) (p-1)(q-1) (p−1)(q−1)的值来攻击RSA。但这种攻击没有分解n容易。
对于持有极端怀疑态度的人来说,有些RSA的变型已经被证明和大数分解同样困难。分解 n n n是最显而易见的攻击方法。敌方手中有公开秘钥 e e e和模数 n n n,要找到解密密钥 d d d,他们就必须分解 n n n,目前,129位十进制数字的模数是能分解的临界数。所以,n应该大于这个数。
对于密码分析者来说,有可能尝试每一种可能的d,直到获得正确的一个。这种穷举攻击还没有试图分解 n n n更有效。
随着时间的推移,声称已经找到破译RSA的简单方法,但直到现在这些宣称还没有强有力的证据。
还有其他的担心,大多数用于计算素数 p p p和 q q q的算法是有概率的,假如 p p p和 q q q不是素数又如何?首先可以找出这件事发生尽可能小的概率。如果不是素数,这就意味着加密和解密均不能正确的工作,可以立即放弃。出现这种问题的主要原因是素性检测是基于概率来检测的。
五、对RSA的选择密文攻击
有些攻击专门针对RSA的实现。他们不攻击算法本身,而是攻击协议。仅使用RSA而不重视它的实现时不够的。实现的细节其实也很重要
情形1——攻击协议:Eve在Alice的通信过程中进行窃听,设法成功选取一个用她的公开秘钥加密的密文
c
c
c,Eve想读出消息。从数学角度来说,她想得到
m
m
m,这里:
m
=
c
d
m=c^d
m=cd为了恢复
m
m
m,首先先选取一个随机数
r
r
r,满足
r
r
r小于
n
n
n。他得到的Alice的公开秘钥
e
e
e,然后计算:
x
=
r
e
m
o
d
n
x=r^emodn
x=r以上是关于密码学——公钥密码体系之RSA算法2的主要内容,如果未能解决你的问题,请参考以下文章