Acwing第 2 场周赛605 题解
Posted 辉小歌
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了Acwing第 2 场周赛605 题解相关的知识,希望对你有一定的参考价值。
做了两道,看了一下第三道题目直接撤了,不过第三道题目好像之前在哪见过。
好像是个原题,不过还是不会。
A: 3626. 三元一次方程 【暴力】
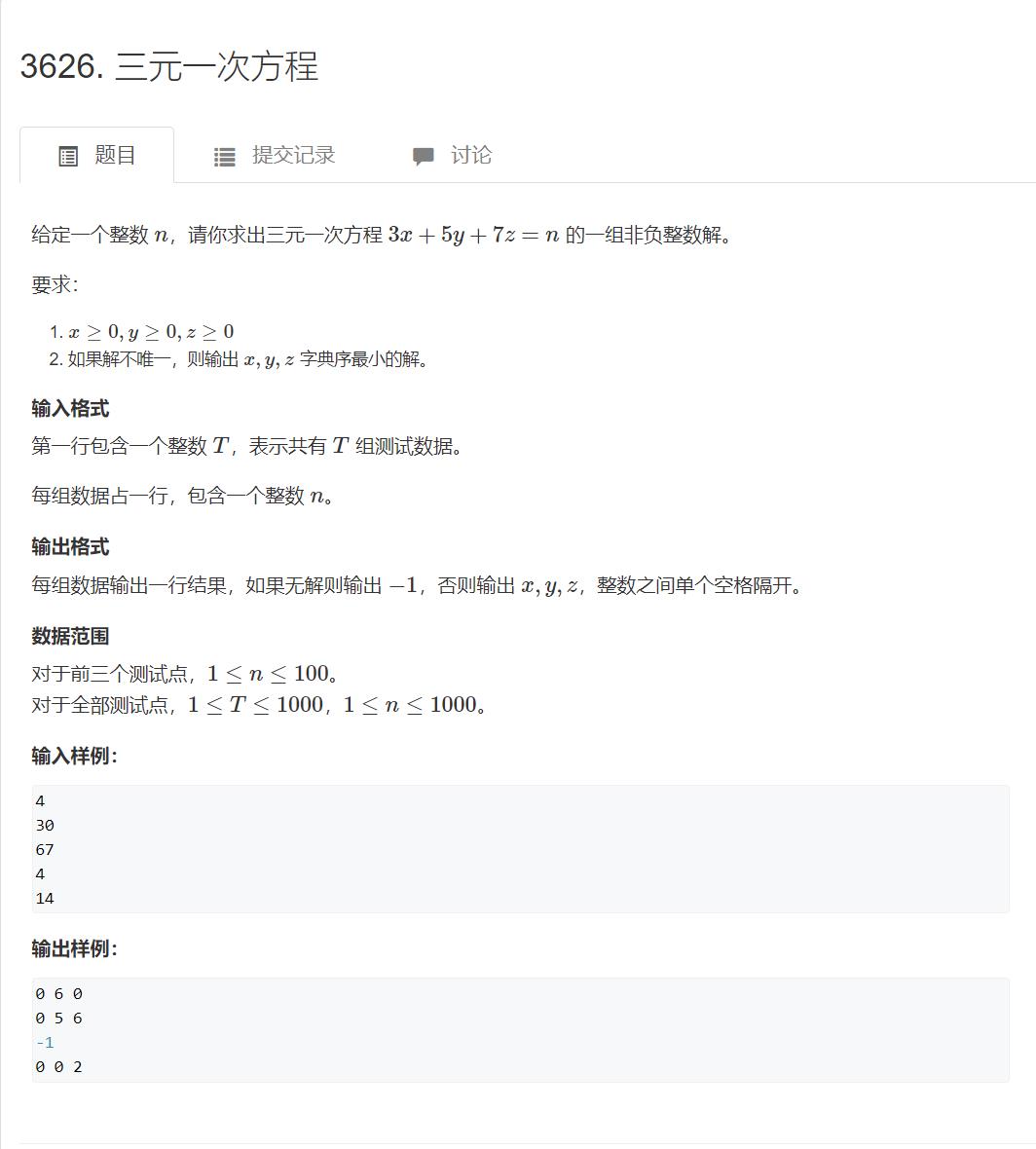
题目地址
这道题居然花费了我十分钟左右,题目数据范围很小直接三重循环暴力就行。
刚开始想复杂了,花费了不少时间,当看到2分钟就有人AC的时候,我知道了这绝对是一个签到。
果断转换思维,打暴力。
#include<cstdio>
#include<iostream>
#include<vector>
#include<map>
#include<set>
#include<string>
#include<cstring>
#include<queue>
using namespace std;
const int N=10;
typedef long long int LL;
int a=3,b=5,c=7;
int main(void)
{
int t; cin>>t;
while(t--)
{
int x; cin>>x;
bool flag=false;
for(int i=0;i<=350;i++)
{
for(int j=0;j<=250;j++)
{
for(int z=0;z<=200;z++)
{
if(i*a+j*b+z*c==x)
{
printf("%d %d %d\\n",i,j,z);
flag=true;
break;
}
}
if(flag) break;
}
if(flag) break;
}
if(!flag) cout<<-1<<endl;
}
return 0;
}
B: 3627. 最大差值 【模拟 / 前缀和】
本来想直接模拟,数据范围很大,于是想到了大根堆用优先队列第一个取出来后,再取k次。
后来一想前缀和可以轻松搞定,果断用前缀和。
#include<cstdio>
#include<iostream>
#include<vector>
#include<map>
#include<set>
#include<string>
#include<cstring>
#include<algorithm>
#include<queue>
using namespace std;
const int N=1e5*2+10;
typedef long long int LL;
LL a[N],s[N];
int main(void)
{
int t; cin>>t;
while(t--)
{
int n,k; scanf("%d%d",&n,&k);
memset(s,0,sizeof s);
for(int i=1;i<=n;i++) scanf("%lld",&a[i]);
sort(a+1,a+n+1);
for(int i=1;i<=n;i++) s[i]=s[i-1]+a[i];//前缀和
LL ans=a[n];
if(k>=(n-1)) ans+=s[n-1];//如果k大于等于剩余的数的数量 直接加完。
else ans+=s[n-1]-s[n-1-k];//否则从 n-1 到n-1-k 取一个长度为k的区间
cout<<ans<<endl;
}
return 0;
}
C: 3628. 边的删减 【最短路径树】
在讲解题目之前,需要直到的前置知识:
- 最短路径的概念: 一个指定的顶点出发,计算从该顶点出发到其他所有顶点的最短路径。
- 最小生成树(Minimum Spanning Tree)简称MST: 有n个点我们选n-1条边可以将所有的点联通,且其权值之和最小。
- 最短路径树(Shortest Path Tree)简称SPT: 是一种使用最短路径算法生成的数据结构树。
- 所谓最短路径树,就是对于给定的源点 ,求出它到所有结点的最短路径,并且通过前驱来标记每个结点是从哪个结点过来的,如果有多 条长度相等的最短路径时,取其中一条,这样整个图就变成了一棵以源点为根结点的树,这棵树就叫最短路径树。
- 需要注意的是,最短路径树是原图的一棵生成树,并且要求原图一定是一个连通图。
本题考察的知识点就是最短路经树,大致思路跑一遍的Dijkstra()求出来,各个点到1的最短距离。
遍历一下图,找到一个最多保留k条边的最短路树,那么我们的最优状态是k+1个点。
如果 dist[b]=dist[a]+w说明这是一条最短路上的边。
y总代码:
#include <iostream>
#include <cstring>
#include <algorithm>
#include <queue>
#include <vector>
#define x first
#define y second
using namespace std;
typedef long long LL;
typedef pair<LL, int> PII;
const int N = 100010, M = 200010;
int n, m, k;
int h[N], e[M], w[M], id[M], ne[M], idx;
LL dist[N];
bool st[N];
vector<int> ans;
void add(int a, int b, int c, int d) // 添加一条边a->b,边权为c
{
e[idx] = b, w[idx] = c, id[idx] = d, ne[idx] = h[a], h[a] = idx ++ ;
}
void dijkstra() // 求1号点到n号点的最短路距离
{
memset(dist, 0x3f, sizeof dist);
dist[1] = 0;
priority_queue<PII, vector<PII>, greater<PII>> heap;
heap.push({0, 1});
while (heap.size())
{
auto t = heap.top();
heap.pop();
int ver = t.second, distance = t.first;
if (st[ver]) continue;
st[ver] = true;
for (int i = h[ver]; i != -1; i = ne[i])
{
int j = e[i];
if (dist[j] > dist[ver] + w[i])
{
dist[j] = dist[ver] + w[i];
heap.push({dist[j], j});
}
}
}
}
void dfs(int u)
{
st[u] = true;
for (int i = h[u]; ~i; i = ne[i])
{
int j = e[i];
if (!st[j] && dist[j] == dist[u] + w[i])//如果这是一条最短路径上的边
{
if (ans.size() < k) ans.push_back(id[i]);//加进来
dfs(j);
}
}
}
int main()
{
scanf("%d%d%d", &n, &m, &k);
memset(h, -1, sizeof h);
for (int i = 1; i <= m; i ++ )
{
int a, b, c;
scanf("%d%d%d", &a, &b, &c);
add(a, b, c, i), add(b, a, c, i);
}
dijkstra();
memset(st, 0, sizeof st);
dfs(1);
printf("%d\\n", ans.size());
for (auto x: ans) printf("%d ", x);
return 0;
}
以上是关于Acwing第 2 场周赛605 题解的主要内容,如果未能解决你的问题,请参考以下文章

