33线性空间07——四个基本子空间的基与维数
Posted 炫云云
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了33线性空间07——四个基本子空间的基与维数相关的知识,希望对你有一定的参考价值。
- 线性空间01——线性空间、线性相关、线性无关、基和维数、极大线性无关
- 线性空间02——坐标、坐标变换与基变换、过度矩阵
- 线性空间03——子空间、子空间的交与和、生成子空间、 子空间的维数公式
- 线性空间04——子空间的直和、n个子空间的直和、直和分解、直和补
- 线性空间05——列空间和零空间、维数
- 线性空间06——行空间和左零空间
- 线性空间07——四个基本子空间的基与维数_
四个基本子空间的基
设 A A A 是一个 m × n m \\times n m×n 阶阵,考虑
列空间(column space) : C ( A ) = { y ∈ R m ∣ y = A x , ∃ x ∈ R n } C(A)=\\left\\{\\mathbf{y} \\in \\mathbb{R}^{m} \\mid \\mathbf{y}=A \\mathbf{x}, \\exists \\mathbf{x} \\in \\mathbb{R}^{n}\\right\\} C(A)={y∈Rm∣y=Ax,∃x∈Rn}
行空间(row space) : C ( A T ) = { y ∈ R n ∣ y = A T x , ∃ x ∈ R m } C\\left(A^{T}\\right)=\\left\\{\\mathbf{y} \\in \\mathbb{R}^{n} \\mid \\mathbf{y}=A^{T} \\mathbf{x}, \\exists \\mathbf{x} \\in \\mathbb{R}^{m}\\right\\} C(AT)={y∈Rn∣y=ATx,∃x∈Rm}
零空间(nullspace) : N ( A ) = { x ∈ R n ∣ A x = 0 } N(A)=\\left\\{\\mathbf{x} \\in \\mathbb{R}^{n} \\mid A \\mathbf{x}=\\mathbf{0}\\right\\} N(A)={x∈Rn∣Ax=0}
左零空间(left nullspace) : N ( A T ) = { x ∈ R m ∣ A T x = 0 } = { x ∈ R m ∣ x T A = 0 } N\\left(A^{T}\\right)=\\left\\{\\mathbf{x} \\in \\mathbb{R}^{m} \\mid A^{T} \\mathbf{x}=\\mathbf{0}\\right\\}=\\left\\{\\mathbf{x} \\in \\mathbb{R}^{m} \\mid \\mathbf{x}^{T} A=\\mathbf{0}\\right\\} N(AT)={x∈Rm∣ATx=0}={x∈Rm∣xTA=0}
注:
(1) C ( A T ) C\\left(A^{T}\\right) C(AT) 是 A A A 的行向量的全部线性组合.
(2) C ( A ) C(A) C(A) 和 N ( A T ) N\\left(A^{T}\\right) N(AT) 是 R m \\mathbb{R}^{m} Rm 的子空间. C ( A T ) C\\left(A^{T}\\right) C(AT) 和 N ( A ) N(A) N(A) 是 R n \\mathbb{R}^{n} Rn 的子空间.
C(A)列空间
矩阵的列空间包含它所有列向量的线性组合,对于 A A A 是一个 m × n m \\times n m×n 矩阵而言,有n个列向量,这些向量都有m个分量,所以 C ( A ) C(A) C(A)是 R m R^m Rm 的子空间。
秩表示主元数量,也表明了列向量组中的一组线性无关的向量,所以 d i m C ( A ) = r = r ( A ) dim C(A)=r=r(A) dimC(A)=r=r(A),一组基就是主元所在列向量即A的主列向量。


C ( A T ) C(A^T) C(AT) 行空间
矩阵的行空间包含它所有行向量的线性组合, 对于 A A A 是一个 m × n m \\times n m×n 矩阵而言,有 m m m个行向量, 这些向量都有n个分量, 所以 C ( A T ) C\\left(A^{T}\\right) C(AT) 是 R n R^{n} Rn 的子空间。
秩是行最简阶梯矩阵 R R R主列数 ,行最简阶梯矩阵只进行了行变换,没有改变这个矩阵的行空间,因此矩阵A和矩阵R的行空间应该是一同一个子空间。所以 dim C ( A T ) = r = r ( A ) \\operatorname{dim} C\\left(A^{T}\\right)=r=r(A) dimC(AT)=r=r(A), 一组基就是R矩阵的前 r r r行。
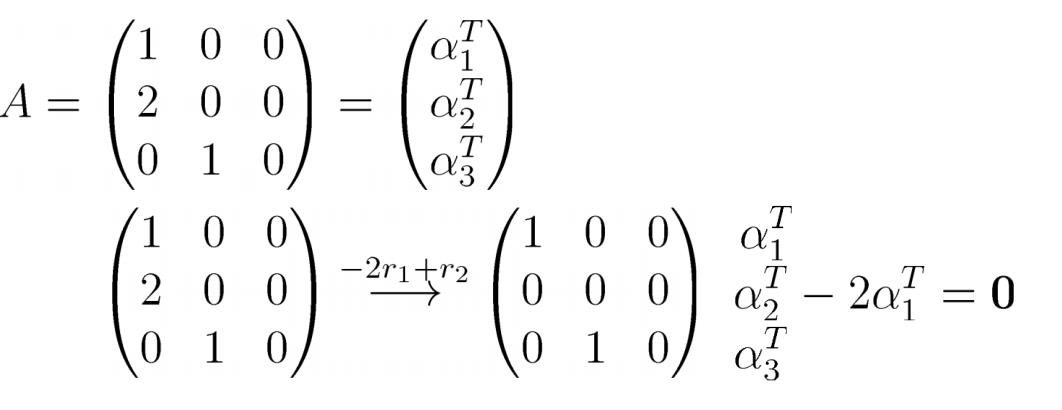
可以看出 α 2 T \\alpha_{2}^{T} α2T 可用 α 1 T , α 3 T \\alpha_{1}^{T}, \\alpha_{3}^{T} α1T,α3T 线性表出, α 1 T , α 3 T \\alpha_{1}^{T}, \\alpha_{3}^{T} α1T,α3T 是 C ( A T ) C\\left(A^{T}\\right) C(AT) 的基.

N(A)零空间
零空间是方程 A x = 0 Ax=0 Ax=0的所有解向量构成的空间,A矩阵列数 n n n决定了解向量 x x x具有n个分量,所以,零空间是 R n R^n Rn 的子空间。
求零空间的时候我们需要知道总共有多少个自由变量,所以自由变量 n − r n-r n−r 就是零空间的维数, d i m N ( A ) = n − r dim N(A)=n-r dimN(A)=n−r ,一组基就是特解。
零空间和列空间的维数关系是:
d
i
m
(
C
(
A
)
)
+
d
i
m
(
N
(
A
)
)
=
r
+
(
n
−
r
)
=
n
dim(C(A))+dim(N(A))=r+(n-r)=n
dim(C(A))+dim(N(A))=r+(n−r)=n
N ( A T ) N(A^T) N(AT) 左零空间
左零空间就是将A进行转置,得到的转置矩阵是n行m列,秩不变, 所以有
m
−
r
m-r
m−r 个自由变量, 所以
dim
N
(
A
T
)
=
m
−
r
\\operatorname{dim} N\\left(A^{T}\\right)=m-r
dimN(AT)=m−r, 转置之后解向量
x
x
x 具有m个分量,所以是
以上是关于33线性空间07——四个基本子空间的基与维数的主要内容,如果未能解决你的问题,请参考以下文章