优化理论13----黄金分割法单峰函数python实现及验证

Posted 2021-06-24 炫云云

一维搜索——黄金分割法

文章目录

• 一维搜索——黄金分割法
• • 无约束一维极值问题
  • 单峰函数
  • • • 定义：
      • 形象地描述如图：
  • 黄金分割法
  • 对黄金分割法的理论阐述
  • python实现及验证
  • 参考资料

最优化知识笔记整理汇总，超级棒

无约束一维极值问题

无约束一维极值问题可简单表述为：
$$\begin{gathered} \min f(x),x\in \mathrm{R}, \\ \text{ or }\min f(x),x\in \left[x_1,x_2\right] \end{gathered}$$
其中 $x$ 为一维变量，相应的 $f(x)$ 为一维变量 $x$ 的函数。

如果自变量的范围为整个实数区间，此时的优化问题为求函数的最小值，是一个全局优化问题。我们考虑的优化问题是以下两种情况：

（1）在自变量的范围为整个实数区间的前提下，求函数的任意一个极值；

（2）在自变量的范围为给定区间的前提下，求函数的任意一个极值。

求解无约束一维极值问题常使用一维搜索法。一维搜索即沿着某一已知方向求目标函数的极小点，其方法是根据已知点通过迭代公式求得新的点，而新的点比当前点更优。

单峰函数

定义：

设$f$是定义在闭区间$[a,b]$上的一元函数，$x^{\ast }$是$f$在$[a,b]$上的极小点，并且对于任意的$x_1,x_2$属于$[a,b]$,$x_1<x_2$;

若当$x_2<=x^{\ast }$ 时，$f(x_1)>f(x_2)$, 当$x^{\ast }<=x_1$时，$f(x_2)>f(x_1)$ 则称$f$是在闭区间[a,b]上的单峰函数。

形象地描述如图：

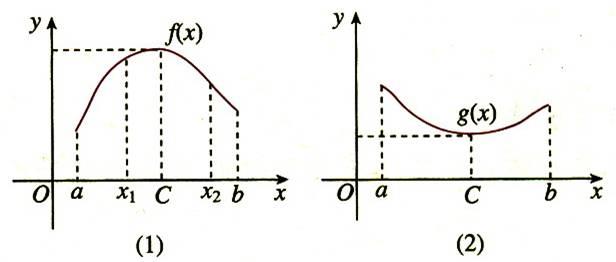
图中f(x)和g(x)均为单峰函数，即在一个区间上存在一个极值点可以将函数明确地分成两半具有单调性的曲线。可以看到，单峰只是一个形象的称呼，也有单谷函数（区间）的称谓

黄金分割法

黄金分割法就是在单峰（谷）区间内搜索出最优解的算法，具体算法步骤如下图：

• 原理：极小点包含于搜索区间内，可以不断地缩小搜索区间，就可以使搜索区间的端点逼近到极小点。

如图所示， $[a,b]$ 为搜索区间，黄金分割法首先根据黄金比例产生两个内点 $x_1,x_2$。

$x_1=a+0.382\ast (b-a)$

$x_2=a+0.618\ast (b-a)$

然后根据 $f\left(x_1\right),f\left(x_2\right)$ 的大小关系来重新选择搜索区间。

1. 若 $f\left(x_1\right)<f\left(x_2\right)$ ，则搜索区间变为 $\left[x_1,b\right]$ ；
2. 若 $f\left(x_1\right)>f\left(x_2\right)$ ，则搜索区间变为 $\left[a,x_2\right]$ 。

• 算法步骤

【1】选定初始区间 $\left[a_1,b_1\right]$ 及精度 $\epsilon >0$ ，令 $\alpha =0.618$,计算试探点：

${\lambda }_1=a_1+(1-\alpha )\ast \left(b_1-a_1\right)$

${\mu }_1=a_1+\alpha \ast \left(b_1-a_1\right)$

并令 $k=1$ 。

【2】若 $b_k-a_k<\epsilon$ ，则停止计算。最优解$x^{\ast }\in [a_k,b_k]$,可取 $x^{\ast }=1/2\ast (a_k$

一维搜索 黄金分割法

OpenCV-单峰三角阈值法Thresh_Unimodal

OpenCV-单峰三角阈值法Thresh_Unimodal

模拟退火

机器学习实战4：基于马尔科夫随机场的图像分割(附Python代码)

优化理论05----最速下降法最速下降法思想python实现