66----曲面的方程柱坐标球坐标曲面的参数方程
Posted 炫云云
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了66----曲面的方程柱坐标球坐标曲面的参数方程相关的知识,希望对你有一定的参考价值。
文章目录
曲面的一般方程
形形色色的曲面

回顾:平面是最简单的曲面
平面可以看作是具有某种约束的点的几何轨迹,其中约束条件是:
动点到定点的连线始终与一定直线垂直 .
平面的一般方程: A x + B y + C z + D = 0 A x+B y+C z+D=0 Ax+By+Cz+D=0.
这个三元一次方程描述平面上所有点的共同性质:
(1) 满足方程的点都在平面上;
(2) 平面上点的坐标满足方程.
平面表示为点的集合: S = { ( x , y , z ) ∈ R 3 ∣ A x + B y + C z + D = 0 } S=\\left\\{(x, y, z) \\in \\mathbb{R}^{3} \\mid A x+B y+C z+D=0\\right\\} S={(x,y,z)∈R3∣Ax+By+Cz+D=0}
曲面可以看作是具有某种约束的点的几何轨迹 .
1、曲面的一般方程
例1
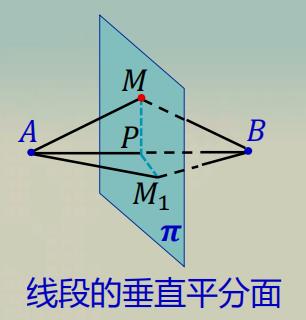
一动点到两定点 A ( x 1 , y 1 , z 1 ) A\\left(x_{1}, y_{1}, z_{1}\\right) A(x1,y1,z1) 和 B ( x 2 , y 2 , z 2 ) B\\left(x_{2}, y_{2}, z_{2}\\right) B(x2,y2,z2) 始终保持相等距离,求这动点的轨迹方程 .
【解】 设动点为
M
(
x
,
y
,
z
)
,
M(x, y, z),
M(x,y,z), 由约束条件知
∣
A
M
∣
=
∣
B
M
∣
|A M|=|B M|
∣AM∣=∣BM∣
由两点距离公式知 线段的垂直平分面
(
x
−
x
1
)
2
+
(
y
−
y
1
)
2
+
(
z
−
z
1
)
2
=
(
x
−
x
2
)
2
+
(
y
−
y
2
)
2
+
(
z
−
z
2
)
2
\\sqrt{\\left(x-x_{1}\\right)^{2}+\\left(y-y_{1}\\right)^{2}+\\left(z-z_{1}\\right)^{2}}=\\sqrt{\\left(x-x_{2}\\right)^{2}+\\left(y-y_{2}\\right)^{2}+\\left(z-z_{2}\\right)^{2}}
(x−x1)2+(y−y1)2+(z−z1)2=(x−x2)2+(y−y2)2+(z−z2)2
整理得三元一次方程:
2
(
x
2
−
x
1
)
x
+
2
(
y
2
−
y
1
)
y
+
2
(
z
2
−
z
1
)
z
−
(
x
2
2
+
y
2
2
+
z
2
2
−
x
1
2
−
y
1
2
−
z
1
2
)
=
0
2\\left(x_{2}-x_{1}\\right) x+2\\left(y_{2}-y_{1}\\right) y+2\\left(z_{2}-z_{1}\\right) z-\\left(x_{2}^{2}+y_{2}^{2}+z_{2}^{2}-x_{1}^{2}-y_{1}^{2}-z_{1}^{2}\\right)=0
2(x2−x1)x+2(y2−y1)y+2(z2−z1)z−(x22+y22+z22−x12−y12−z12)=0
这说明动点的轨迹是一个平面 .
例2
到一定点 M 0 ( x 0 , y 0 , z 0 ) M_{0}\\left(x_{0}, y_{0}, z_{0}\\right) M0(x0,y0,z0) 的距离等于常数 R ( R > 0 ) R(R>0) R(R>0) 的动点的轨迹是球面 . 求这球面的方程 .
【解】 设动点为
M
(
x
,
y
,
z
)
,
M(x, y, z),
M(x,y,z), 则
∣
M
0
M
∣
=
R
\\left|M_{0} M\\right|=R
∣M0M∣=R,由两点距离公式知
(
x
−
x
0
)
2
+
(
y
−
y
0
)
2
+
(
z
−
z
0
)
2
=
R
\\sqrt{\\left(x-x_{0}\\right)^{2}+\\left(y-y_{0}\\right)^{2}+\\left(z-z_{0}\\right)^{2}}=R
(x−x0)2+(y−y0)2+(z−z0)2=R
整理得三元方程:
(
x
−
x
0
)
2
+
(
y
−
y
0
)
2
+
(
z
−
z
0
)
2
=
R
2
\\left(x-x_{0}\\right)^{2}+\\left(y-y_{0}\\right)^{2}+\\left(z-z_{0}\\right)^{2}=R^{2}
(x−x0)