优化理论14----二分法二分法与黄金分割法比较python实现
Posted 炫云云
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了优化理论14----二分法二分法与黄金分割法比较python实现相关的知识,希望对你有一定的参考价值。
一维搜索——二分法
最优化知识笔记整理汇总,超级棒
二分法
同前面的方法一样,仍然要求函数 f f f 在区间 [ a 0 , b 0 ] [a_0,b_0] [a0,b0] 上位单峰函数。另外,二分法还要求函数为连续可微的,因为要使用到一阶导数 f ′ f' f′ 。
求解的过程为:
1)确定初始区间的中点 x ( 0 ) = ( a 0 + b 0 ) / 2 x^{(0)}=(a_0+b_0)/2 x(0)=(a0+b0)/2 。
2)计算函数在 x ( 0 ) x^{(0)} x(0) 处的一阶导数 f ′ ( x ( 0 ) ) f'(x^{(0)}) f′(x(0))
- 如果 f ′ ( x ( 0 ) ) > 0 f'(x^{(0)})>0 f′(x(0))>0 ,说明极小点在 x ( 0 ) x^{(0)} x(0) 左侧,区间压缩为 [ a 0 , x ( 0 ) ] [a_0,x^{(0)}] [a0,x(0)]
- 如果 f ′ ( x ( 0 ) ) < 0 f'(x^{(0)})<0 f′(x(0))<0 ,说明极小点在 x ( 0 ) x^{(0)} x(0)右侧,区间压缩为 [ x ( 0 ) , b 0 ] [x^{(0)},b_0] [x(0),b0]
- 如果 f ′ ( x ( 0 ) ) = 0 f'(x^{(0)})=0 f′(x(0))=0,说明极小点为 x ( 0 ) x^{(0)} x(0)
按照如上的方式,在第k次迭代过程中计算相应的一阶导数并判断极小点可能在的区间。
二分法与黄金分割法比较
二分法是用来求根的,而黄金分割法是用来求极值的。如果非要用黄金分割法来求根的话会比二分法慢一个常数
单峰函数求极值问题:(黄金分割在上,二分法在下),明显黄金分割更快
注意:用阴影表示的“可能区域”里面始终都有三个已经计算过的点。
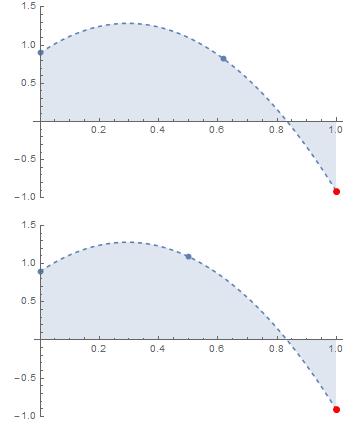
单根函数求根问题:(黄金分割在上,二分法在下),明显二分法更快
注意:用阴影表示的“可能区域”里面始终都有两个已经计算过的点。
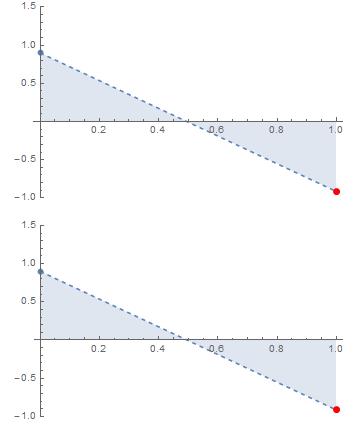
分割的越“均衡”,算法执行得就越快。求根问题中的二分法和求极值问题中的黄金分割法都满足每次更新的“可行区域”和上一个“可行区域”是相似的.
二分法
假设
f
(
x
)
f(x)
f(x) 是一个连续可微凸函数。为了求解步长,解决:
α
ˉ
:
=
arg
min
α
f
(
x
ˉ
+
α
d
ˉ
)
\\bar{\\alpha}:=\\arg \\min _{\\alpha} f(\\bar{x}+\\alpha \\bar{d})
αˉ:=argαminf(xˉ+αdˉ)
其中
x
ˉ
\\bar{x}
xˉ是我们当前的迭代,
d
ˉ
\\bar{d}
dˉ是试图最小化f(x)的算法产生的当前方向。假设
d
ˉ
\\bar{d}
dˉ是
f
(
x
)
f(x)
f(x)在
x
=
x
ˉ
x=\\bar{x}
x=xˉ处的下降方向。有
f
(
x
ˉ
+
ϵ
d
ˉ
)
<
f
(
x
ˉ
)
对于所有
ϵ
>
0
并且充分小
f(\\bar{x}+\\epsilon \\bar{d})<f(\\bar{x}) ~~~~\\text { 对于所有 } \\epsilon>0 \\text { 并且充分小 }
f(xˉ+ϵdˉ)<f(xˉ) 对于所有 ϵ>0 并且充分小
设
h
(
α
)
:
=
f
(
x
ˉ
+
α
d
ˉ
)
h(\\alpha):=f(\\bar{x}+\\alpha \\bar{d})
h(α):=f(xˉ+αdˉ),因此,
h
(
α
)
h(\\alpha)
h(α)是标量变量
α
\\alpha
α中的一个凸函数,我们的问题是求解
α
ˉ
=
arg
min
α
h
(
α
)
\\bar{\\alpha}=\\arg \\min _{\\alpha} h(\\alpha)
αˉ=argαminh(α)
让
h
′
(
α
ˉ
)
=
0
,
h^{\\prime}(\\bar{\\alpha})=0,
h′(αˉ)=0, 其中
h
′
(
α
)
=
∇
f
(
x
ˉ
+
α
d
ˉ
)
T
d
ˉ
h^{\\prime}(\\alpha)=\\nabla f(\\bar{x}+\\alpha \\bar{d})^{T} \\bar{d}
h′(α)=∇f(xˉ+αdˉ)Tdˉ
命
题
1
\\large\\color{magenta}{\\boxed{\\color{brown}{命题1} }}
命题1
h
′
(
0
)
=
0
h^{\\prime}(0)=0
h′(0)=0
因为 h ( α ) h(\\alpha) h(α) 是一个凸函数,我们有:
命 题 2 \\large\\color{magenta}{\\boxed{\\color{brown}{命题2} }} 命题2 h ′ ( α ) h^{\\prime}(\\alpha) h′(α)是 α \\alpha α的单调递增函数。
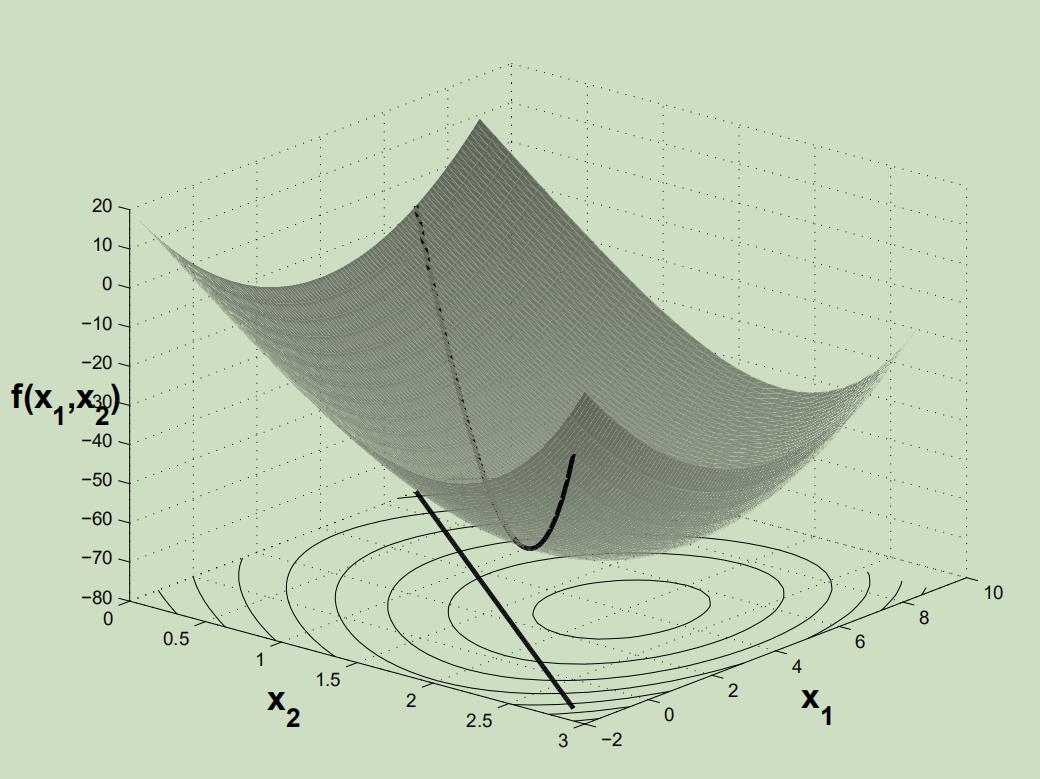
图3给出了一个需要优化的双变量凸函数示例。图4显示了函数 h ( α ) h(\\alpha) h(α) ,通过将图3的函数限制在该图中所示的直线上得到的。注意,从图4中可以看出 h ( α ) h(\\alpha) h(α)是凸的。因此它的一阶导数 h ′ ( α ) h^{\\prime}(\\alpha) h′(α)是一个单调递增的函数。如图5所示
图
3
待
优
化
的
凸
函
数
。
图3 待优化的凸函数。
图3待优化的凸函数。
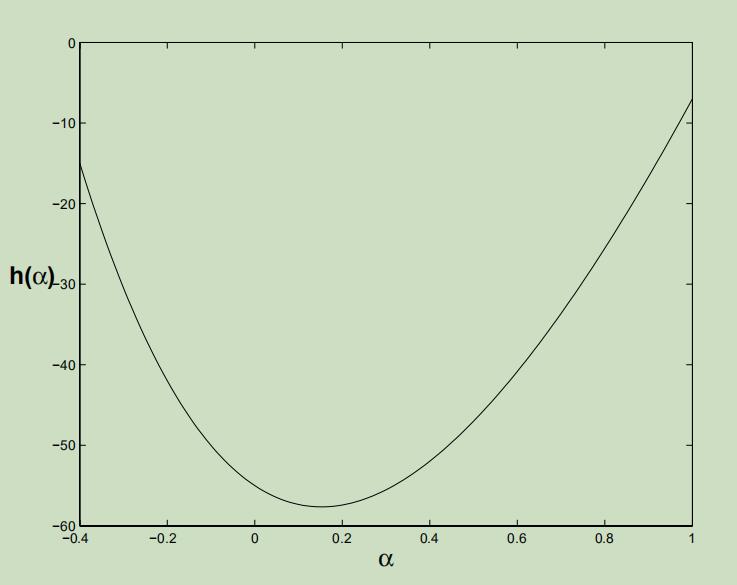
图 4 一 维 函 数 h ( α ) 图4 一维函数h(α) 图4一维函数h(α)
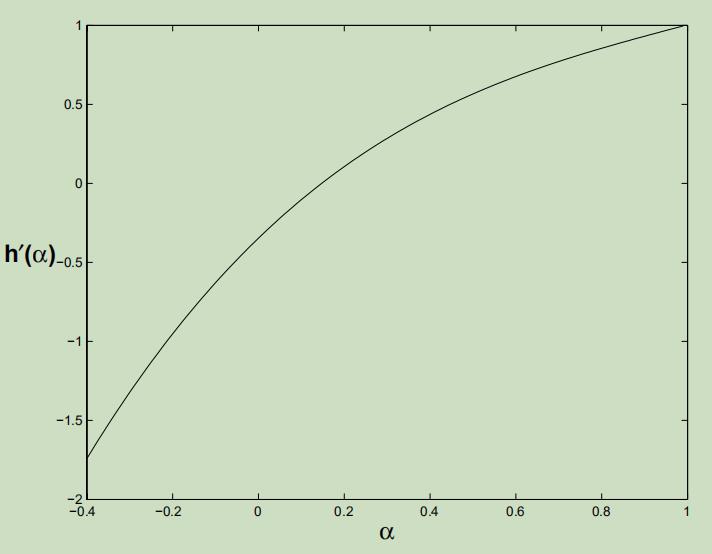
图 5 一 阶 导 数 h ′ ( α ) 是 一 个 单 调 递 增 的 函 数 图5 一阶导数h^{\\prime}(\\alpha)是一个单调递增的函数 图5一阶导数h′(α)是一个单调递增的函数
二分法的思想:
同前面的方法一样,仍然要求函数 f f f 在区间 [ a 0 , b 0 ] [a_0,b_0] [a以上是关于优化理论14----二分法二分法与黄金分割法比较python实现的主要内容,如果未能解决你的问题,请参考以下文章