数据结构--排序

Posted 2021-06-24 水澹澹兮生烟.

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了数据结构--排序相关的知识，希望对你有一定的参考价值。

文章目录

1.排序的概念
2.常见的排序算法

1.排序的概念

排序：所谓排序，就是使一串记录，按照其中的某个或某些关键字的大小，递增或递减的排列起来的操作。
稳定性：在原序列中，r[i]=r[j]，且r[i]在r[j]之前，而在排序后的序列中，r[i]仍在r[j]之前，则称这种排序算法是稳定的；否则称为不稳定的。
在这里插入图片描述
内部排序：将数据一次性加载到内存中。
外部排序：数据元素太多不能同时放在内存中，根据排序过程的要求不能在内外存之间移动数据的排序。

2.常见的排序算法

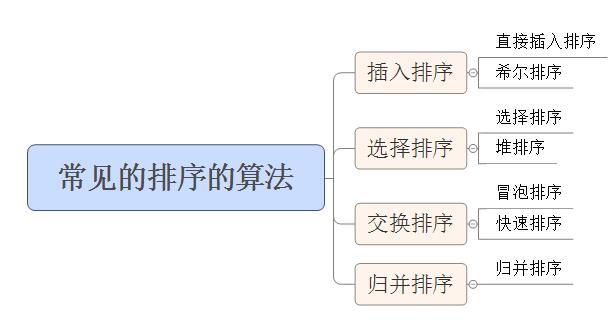
在这里插入图片描述

2.1插入排序–直接插入排序

单个元素的插入
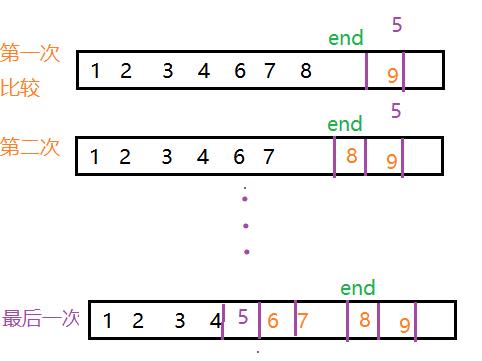
给定一组元素[1，2，3，4，6，7，8，9] ，将5插入这组元素中，首先要进行插入，必须满足原数据已经排好序列，然后从后向前比较(这样可以直接将数据进行向后搬移)，进行插入。如下图：
在这里插入图片描述

while(key<array[end]){
	array[end+1]=array[end];
	end--;
}
array[end+1]=key;

现在我们给出一组无序数据，用进行快速排序。与上面的原理相同，我们可以从数据的第二个数据开始，向前比较。
他的时间复杂度为：O(N^2)
他的稳定性：稳定的
应用场景：在元素个数较少，接近有序


for(int i=1;i<size;i++){
	key=array[i];
	int end=i-1;
	while(end>=0&&key<array[end]){
		array[end+1]=array[end];
	    end--;
    }
    array[end+1]=key;
}

最终实现：

void IsertSort(int array[], int size){
	//表示当前要插入元素在数组中的下标，i位置的元素一定往i之前插入
	for (int i = 1; i < size; i++){
		int key = array[i];//我们要开始插入的元素从第i个开始
		int end = i - 1;//我们的要插入的数组的end=i-1
		while (end>=0&&array[end]>key){
			array[end + 1] = array[end];
			end--;
		}
		array[end+1] = key;
	}
}

2.2插入排序–希尔排序

现在给出一组数据，他的数据量大，且无序，到那时还是要使用插入排序的思想，这时，我们可以借助希尔排序。
希尔排序法：又称缩小增量法。希尔排序法的基本思想是：先选定一个整数，把待排序文件中所有记录分成个组，所有距离为的记录分在同一组内，并对每一组内的记录进行排序。
在这里插入图片描述如何进行分组呢？
此时我们可以间隔着将其进行分组。假设给一个标记gap=3,一下标每间隔3分成一组，进行排序。

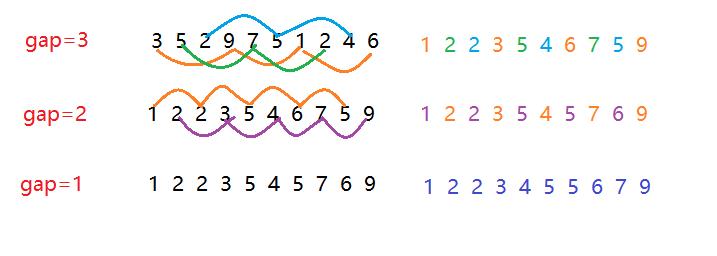
当gap > 1时都是预排序，目的是让数组更接近于有序。当gap == 1时，数组已经接近有序的了。
gap取值：

 int gap=size;
 gap=gap/3+1;

复杂度：O(N^1.3—N2）
稳定性：不稳定
应用场景：数据量大，且无序。

void ShellSort(int array[], int size)
{
	int gap = size;
	while (gap > 0){
	gap=gap/3+1;
		for (int i = gap; i < size; i++){
			int key = array[i];//我们要开始插入的元素从第i个开始
			int end = i - gap;//我们的要插入的数组的end=i-1
			while (end >= 0 && array[end]>key){
				array[end + gap] = array[end];
				end -= gap;
			}
			array[end + gap] = key;
		}
	}
	
}

2.3选择排序–选择排序

选择排序：每一次从待排序的数据元素中选出最小（或最大）的一个元素，存放在序列的起始位置，直到全部待排序的数据元素排完。
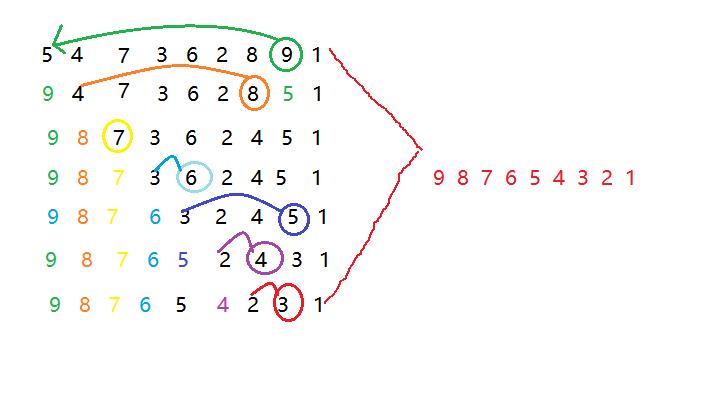
在这里插入图片描述
时间复杂度:O(N^2)
稳定性：不稳定

//降序排序
void SElectSort(int array[], int size){
	
	for (int i = 0; i < size; i++){
		int index = i;
		int max = array[i];
		for (int j = i; j < size; j++){
			if (array[j]>max){
				max = array[j];
				index = j;
			}
		}
		array[index] = array[i];
		array[i] = max;
	}
}

同时对最大值与最小值进行降序排列

//同时调节最大元素与最小元素
void SelectSorttogether(int array[], int size){
	for (int i = 0; i < size; i++){
		int max = array[i];
		int min = array[size - i-1];
		int index_max = i;
		int index_min = size - 1 - i;
		for (int j = i; j < size - i - 1; j++){
			if (array[j]>max){
				max = array[j];
				index_max = j;
			}
			if (array[j] < min){
				min = array[j];
				index_min = j;
			}
		}
		array[index_max] = array[i];
		array[i] = max;
		array[index_min] = array[size - i - 1];
		array[size - i - 1] = min;
		
	}
}

选择排序的缺陷：存在重复比较。–>如何优化？利用堆排序。

2.4选择排序–堆排序

(原理：我的另一篇博客)

void Heapadjustdown(int array[], int size, int parent){
	int temp = 0;
	int child = parent * 2 + 1;//先标记左孩子，一个堆里面不一定又右孩子
	while (child<size){//此时，保证父结点一直存在孩子
		if (child + 1 < size&&array[child + 1] > array[child]){//此时先判定有没有右孩子，在看右孩子是否大于左孩子在对
			child += 1;//标记孩子结点
		}
		if (array[parent] < array[child]){
			//如果此时父结点小于子结点那么进行交换
			temp=array[child]  ;
			array[child] = array[parent];
			array[parent] = temp;
			//此时交换结束后，对其父结点和子结点的位置进行调整
			parent = child;
			child = parent * 2 + 1;
		}
		else{ break; }

	}
}
//堆排序
void Heapsort(int array[], int size){
	int temp = 0;
	//建堆，升序建设大堆，降序建小堆
	//从倒数第一个非叶子结点开始知道根节点的位置向下调整
	int root = size/ 2-1;
	while (root >= 0)
	{
		Heapadjustdown(array, size, root);
		root--;
	}
	//进行完向下调整得到大堆后，我们可以开始利用堆删除进行对堆排序
	int end = size-1;//删除堆顶元素
	while (end>0){
		//1.将堆顶元素于堆尾元素进行交换
		temp = array[0];
		array[0]=array[end];
		array[end] = temp;
		//2.删除堆尾元素
		end--;
		//3.对进行删除完后的堆进行重新向下排序
		Heapadjustdown(array, end+1, 0);
	}
}

2.5交换排序–冒泡排序

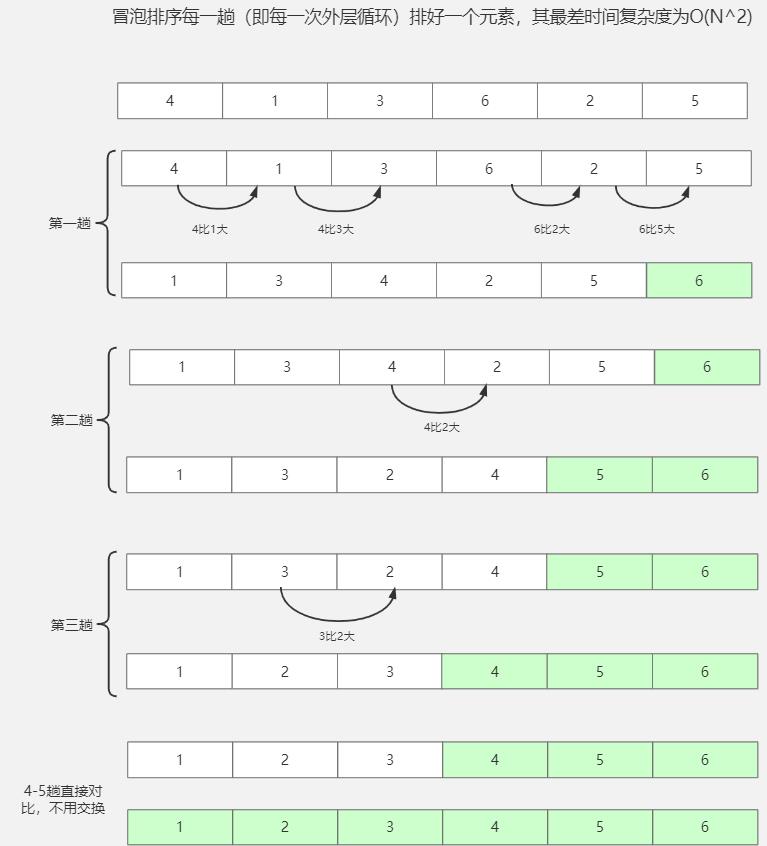
在这里插入图片描述

//冒泡排序,顺序排列
void BubbleSort(int array[], int size){
	int swap = 0;
	for(int i = 0; i < size-1; i++){
		for (int j = 0; j < size - i-1; j++){
			if (array[j]> array[j + 1]){
				swap = array[j];
				array[j] = array[j + 1];
				array[j + 1] = swap;
			}
		}
	}
}

2.6交换排序–快速排序

快速排序是Hoare于1962年提出的一种二叉树结构的交换排序方法，其基本思想为：任取待排序元素序列中的某元素作为基准值，按照该排序码将待排序集合分割成两子序列，左子序列中所有元素均小于基准值，右子序列中所有元素均大于基准值，然后最左右子序列重复该过程，直到所有元素都排列在相应位置上为止。
在这里插入图片描述
现在我们看如何按照基准值来划分：
但是在基准值上的选择是十分重要的，在基准值选择上我们要尽量避免大多数情况下选择最大值或最小值，下面使取基准值的优化(三数取中法)：

int middlenum(int array[], int left, int right){
	int middle = (left + right) / 2;
	if (array[left] < array[right]){
		if (array[middle] < array[left])
			return left;
		else if (array[middle]>array[right])
			return right;
		else
			return middle;
	}
	else{
		if (array[middle]>array[left])
			return left;
		else if (array[middle] < array[right])
			return right;
		else
			return middle;
	}
}

法一：hoare
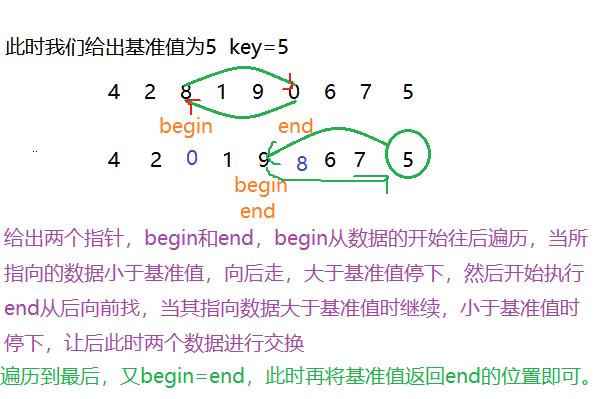
在这里插入图片描述

int partion1(int array[], int left1, int right1){
	int left = left1;
	int right = right1;
	int temp = 0;
	int key = middlenum(array,left,right);
	//交换right与key的位置,将基准值再次放到末位置
	temp = array[right];
	array[right] = array[key];
	array[key] = temp;
	while (right>left){
		if (array[left]<array[right1]){
			left++;
		}
		else{
			if (array[right] >= array[right1]){
				right--;
			}
			else{
				temp = array[left];
				array[left] = array[right];
				array[right] = temp;
			}
		}

	}
	if (left < right1){
		//将基准值于left位置进行交换
		temp = array[right1];
		array[right1] = array[left];
		array[left] = temp;
	}
	return left;
}

法二:挖坑法
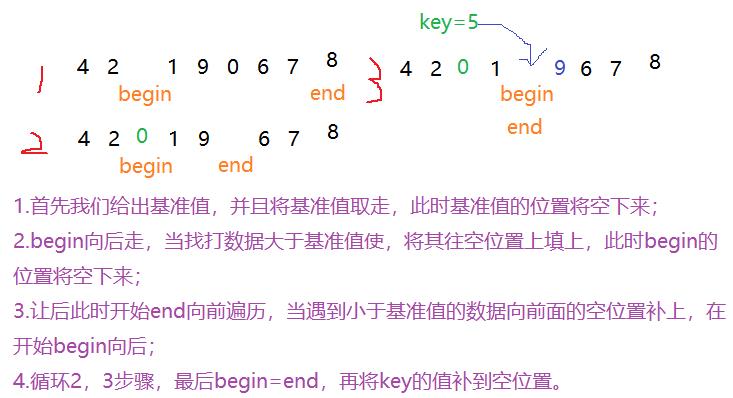
在这里插入图片描述

int partion2(int array[] , int left1, int right1){
	//挖坑法
	int left = left1;
	int right = right1;
	int temp = 0;
	int key = middlenum(array, left, right);
	//交换right与key的位置,将基准值再次放到末位置
	temp = array[right];
	array[right] = array[key];
	array[key] = temp;
	int keynum = array[right1];//将key值进行保存
	while (left < right){
		while (left<right&&array[left] < keynum){
			left++;
		}
		//如果大于，则用此时数据进行填坑
		array[right] = array[left];
		while (left<right&&array[right]>=keynum){
			right--;
		}
		array[left] = array[right];
	}
	//最后将基准值补到空位置上
	array[left] = keynum;
	return left; 
}

法三：前后指针法
在这里插入图片描述

int partion3(int array[], int left, int right){
	int cur = left;
	int prve = cur - 1;
	int key = middlenum(array, left, right);
	//交换right与key的位置,将基准值再次放到末位置
	int temp = array[right];
	array[right] = array[key];
	array[key] = temp;
	while (cur < right){
		if (array[cur] < array[right] && ++prve != cur){
			//交换right与key的位置,将基准值再次放到末位置
			temp = array[prve];
			array[prve] = array[cur];
			array[cur] = temp;
		}
		cur++;
	}
	if (++prve != right){
		temp = array[prve];
		array[prve] = array[right];
		array[right] = temp;
	}
	return prve;
}

快速排序的实现：
1.递归法

void quickSort_hoare(int array[],int left,int right){
	
	int div=0;
	if (right - left < 1){
		return;
	}
	//结束后，我们将基准值左面的进行排序右面的进行排序
	div = partion3(array, left, right);
	//key左面的排序
	quickSort_hoare(array, left, div);
	//key右面的排序
	quickSort_hoare(array, div + 1, right);
}

2.循环的方法
因为每次进行递归，相当于通过层层压栈的方式进行保存起来，我们只需要自己定义一个栈的结构，对每次形成的区间进行保存即可。

  void QuicksortNor(int array[],int size){
  	stack s;
  	stackInit(&s);//对栈进行初始化
  	int left=0;
  	int right=size;
  	int div=0;

  	stackPush(&s,left);//对左边界进行压栈
  	stackPush(&s,right);//对右边界进行压栈


  	while(!StackEmpty(&s)){
  		right=stackTop(&s);//先取有右边界元素
  		stackPop(&s);//移除
  		left=stackTop(&s);
  		stackPop(&s);
  		if(right-left>=1){	
  			div=pation1(array,left,right);
  			//[div+1,rigth],先压右半侧
  			stackpush(&s,div+1);
  			stack(&s,right);
  			//[left,div]
  			stackpush(&s,left);
  			stackpush(&s,div);
  		}else{
  			break;
  		}
  	}
  	stackDestory(&s);//栈的销毁
  }

快排在最好的情况下时间复杂度–O(Nlog2(N)),最坏的情况下–O(N^2)。
空间复杂度最好为–O(log2N),最坏的情况下–O(N)。

2.7归并排序

数量非常大，不能一次性加载到内存中。
1.在学习归并排序中，此时我们要知道给定两组有序数据，将其合并成一组数据。
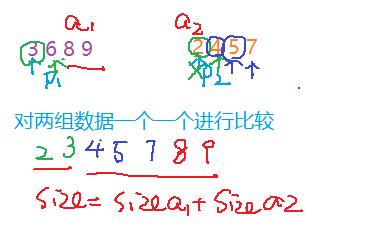
在这里插入图片描述

void meraedata(int array[],int left,int right,int temp[]){
	//现在我们一直一组数据时从[left，mid),另一组数据是从[mid-right)
	int i = 0;
	int begin1 = left;
	int end1 = left + <以上是关于数据结构--排序的主要内容，如果未能解决你的问题，请参考以下文章 
 以下代码片段的时间复杂度是多少？
 ElasticSearch学习问题记录——Invalid shift value in prefixCoded bytes (is encoded value really an INT?)(代码片段
 排序02-直接插入排序法
 markdown 数组排序片段
 Java排序算法 - 堆排序的代码
 Realm和RecyclerView项目排序和自动ViewPager片段通信