基于Ziegler-Nlichols方法的参数整定与PID仿真

Posted 2021-06-24 昔时扬尘处

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了基于Ziegler-Nlichols方法的参数整定与PID仿真相关的知识，希望对你有一定的参考价值。

基于Ziegler-Nlichols方法的参数整定与PID仿真

0研究背景

写在前面

1.本代码基于MATLAB2019a版本，低版本或者不同版本可能会报错，mdl文件或slx文件打开可能会失败；
2.本博客将详细介绍Ziegler-Nlichols方法的PID仿真，如果转载请注明出处；
3.如果本博客恰巧与您的研究有所关联，欢迎您的咨询qq1366196286。

1被控对象的传递函数

$G(s)=\\frac{1}{s(s+2)(s+4)}$

系统数学模型（即传递函数）确定的这种数学模型是在用拉普拉斯变换方法求解微分方程过程中引出来的复域中的数学模型，它不但能等同微分方程反映系统的输入、输出动态特性，而且能间接的反映结构、参数变化时对系统输出的影响。而且传递函数只取决于系统（或元件）的结构和参数，与外界输入无关。基于传递函数模型的传统PID控制经验公式，是Ziegler与Nichols于20世纪40时年代提出的。他们著名的回路整定技术使得PID算法直到现在还被广泛地应用在工业领域内的反馈控制策略中。本博客将以传递函数为背景来介绍基于Ziegler-Nlichols 方法的PID仿真实现。

m函数

 
 clc,
 clear all; %#ok<CLALL> 
 num = [1]; %#ok<NBRAK>
 den = [1 6 8 0];
 sys = tf(num,den);
 isstable(sys) %%判断系统是否稳定，返回值1，说明系统是稳定的，返回值0，则系统不具有稳定性。

运行结果如下：
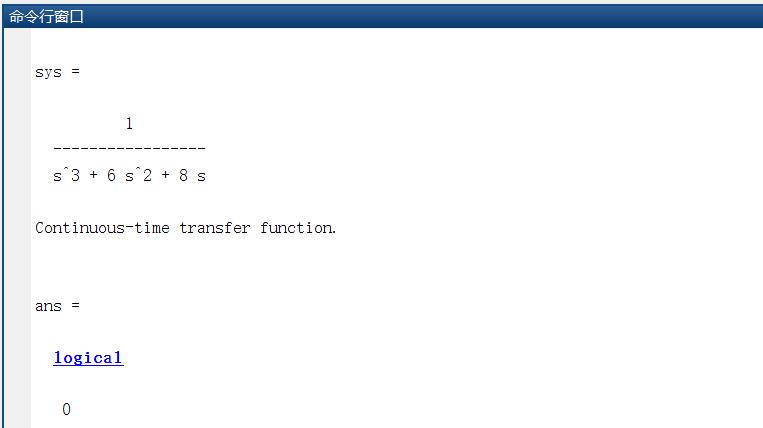
在这里插入图片描述

其中logical的返回值，是判断系统是否稳定的。返回值0，说明系统不具有稳定性。

Simulink仿真文件
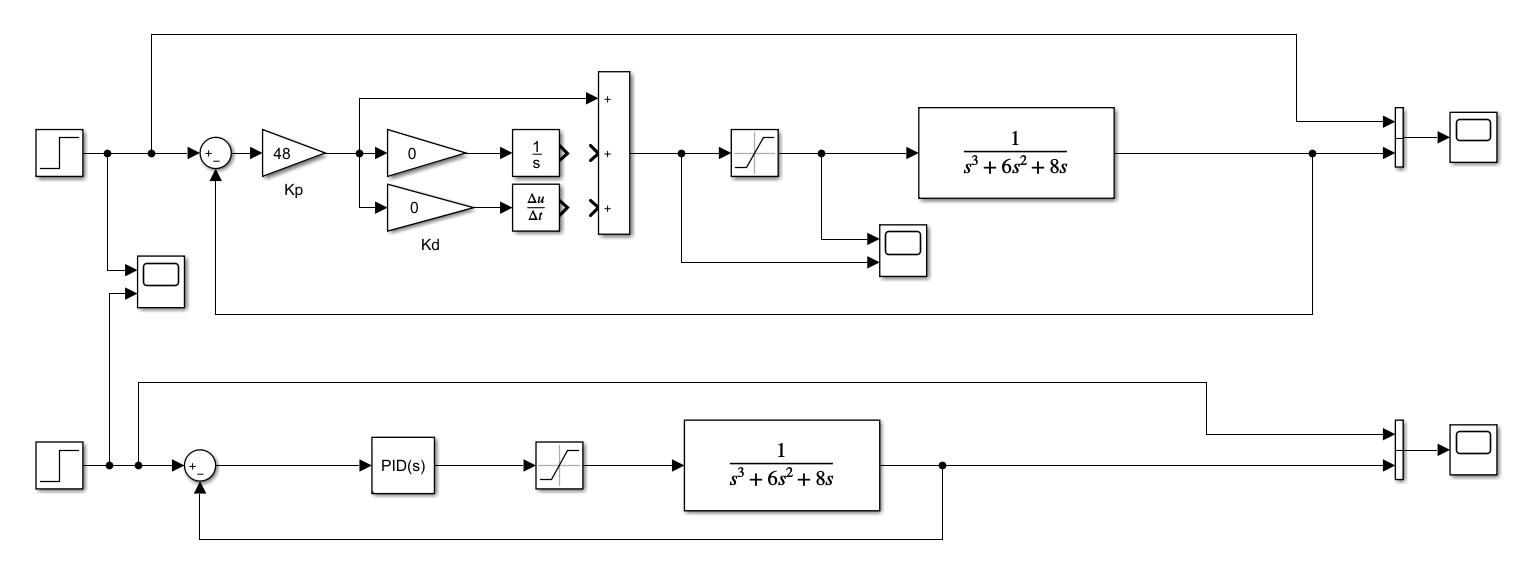
在这里插入图片描述

2Ziegler-Nlichols方法的阶跃响应曲线

大致的整定流程与步骤，如下图所示。其中以基于Ziegler-Nlichols 方法的PID参数整定为基础，也可以前往参数整定的专栏，去进一步了解PID控制器的控制参数对系统的影响作用，链接直达：基于遗传算法的PID参数整定研究。
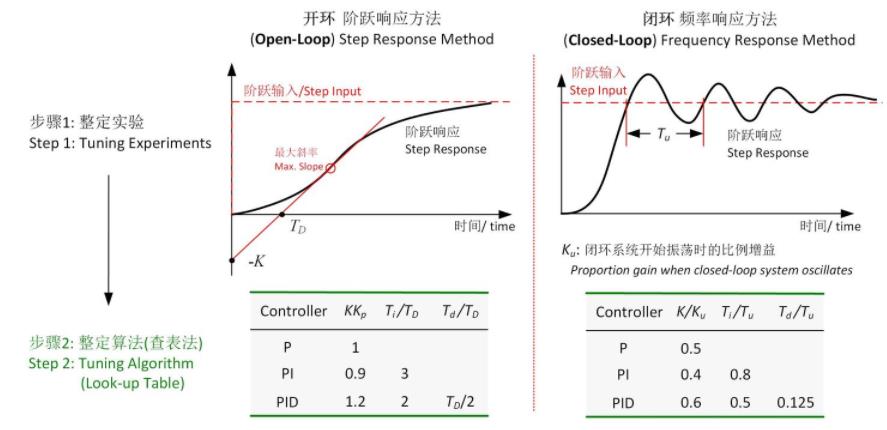
在这里插入图片描述

2.1 Ziegler-Nlichols方法的简单介绍

控制系统在外界干扰作用后，不能恢复到稳定的平衡状态，而出现一种既不衰减，也不发散的等幅振荡过程，这样的过渡过程就称为临界振荡过程，如下图所示。
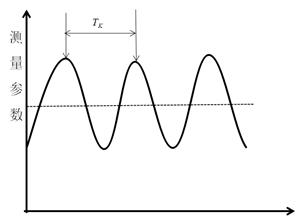
在这里插入图片描述
图临界振荡过程示意图（一般的我们选定3Tk以减小测量误差）

PID控制算法为

$u(t)=\\frac{1}{\\delta_{\\mathrm{k}}}\\left(e+\\frac{1}{T_{\\mathrm{i}}} \\int_{0}^{t} e \\mathrm{~d} t+T_{\\mathrm{D}} \\frac{\\mathrm{d} e}{\\mathrm{~d} t}\\right)$

式中，δk为临界比例度，Ti为积分时间，TD为微分时间

Ziegler-Nlichols方法是根据给定对象的临界状态参数K和T来确定PID控制器的参数，整定公式如表1-l所示。其中，如果单位阶跃响应曲线为S形曲线，则可用此法，否则不能用。此外，适用于临界振幅不大、振荡周期较长的过程控制系统，但有些系统从安全性考虑不允许进行稳定边界试验，如锅炉汽包水位控制系统。还有某些时间常数较大的单容对象，用纯比例控制时系统始终是稳定的，对于这些系统也是无法用临界比例度法来进行参数整定的。

我们在Ziegler-Nlichols方法整定中，首先需要得到的就是临界参数，即在临界状态下，被控量y来回振荡一次所用时间，称为临界周期Tk。被调参数处于临界状态时的比例度，称为临界比例度δk。其次，在上图中的临界振荡过程，可以得到我们所需要的临界比例度δk和临界周期Tk的数值。再次，根据控制器的结果结合表选定经验公式，最后根据经验公式计算出PID控制器各参数的具体数值。具体的实现步骤如下：

Step 1 寻找临界振荡状态，求取临界比例度δk和临界周期Tk。

先把积分时间放至最大，微分时间放至零，比例度放至较大的适当值。“纯P控制参数”，就是使控制系统按纯比例作用的方式投入运行。然后，慢慢地减少比例度，在外界干扰的作用下，细心观察控制器的输出信号和被调参数的变化情况。如果控制过程的曲线波动是衰减的，则把比例度继续调大，如果控制过程的曲线波动是发散的，则应把比例度调小些，直到曲线波动呈等幅振荡为止，从而得到临界比例度δk和临界周期Tk值。即整定口诀说的“等幅振荡出现时，δk值Tk值为临界”。

Step 2 结合控制器的结构形式，按表选定参数计算公式。

表 Ziegler-Nlichols方法的参数整定计算表
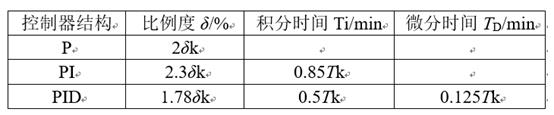
在这里插入图片描述

“按照公式乘系数”即根据得到的δk和Tk值按下表临界比例度法参数计算公式表，来计算调节器的各参数值。

Step 3 先比例调节，后积分调节，最后微分调节。

求得具体的数值后，将比例度调在比计算数值大一些的刻度上，然后把积分时间放至计算值上，然后从大到小地调整积分时间，最后把微分时间放至计算值上，从小到大地调整微分时间。这样的调整次序就是口诀中的“PID顺序不能错”。

Step 4 多次调节参数，观察最佳响应曲线的输出。

最后把比例度减小到计算值上，通过观察曲线，也就是“静观运行勤调整，细心寻求最佳值”。即适当地进行各参数的微调，以达到满意的控制效果。

整定的口诀：

临界整定应用多，纯P运转减参数；

等幅振荡出现时，δk值Tk值为临界；

按照公式乘系数，P、I、D顺序不能错；

静观运行勤调整，细心寻求最佳值。

2.2 Ziegler-Nlichols方法的整定过程

构建闭环控制回路，确定稳定极限。将积分作用和微分作用均断开连接，或者直接在PID控制器模块中将其所对应的控制参数设置为0。即此时被控对象仅存在比例作用，通过调节比例系数，来获取临界震荡状态。
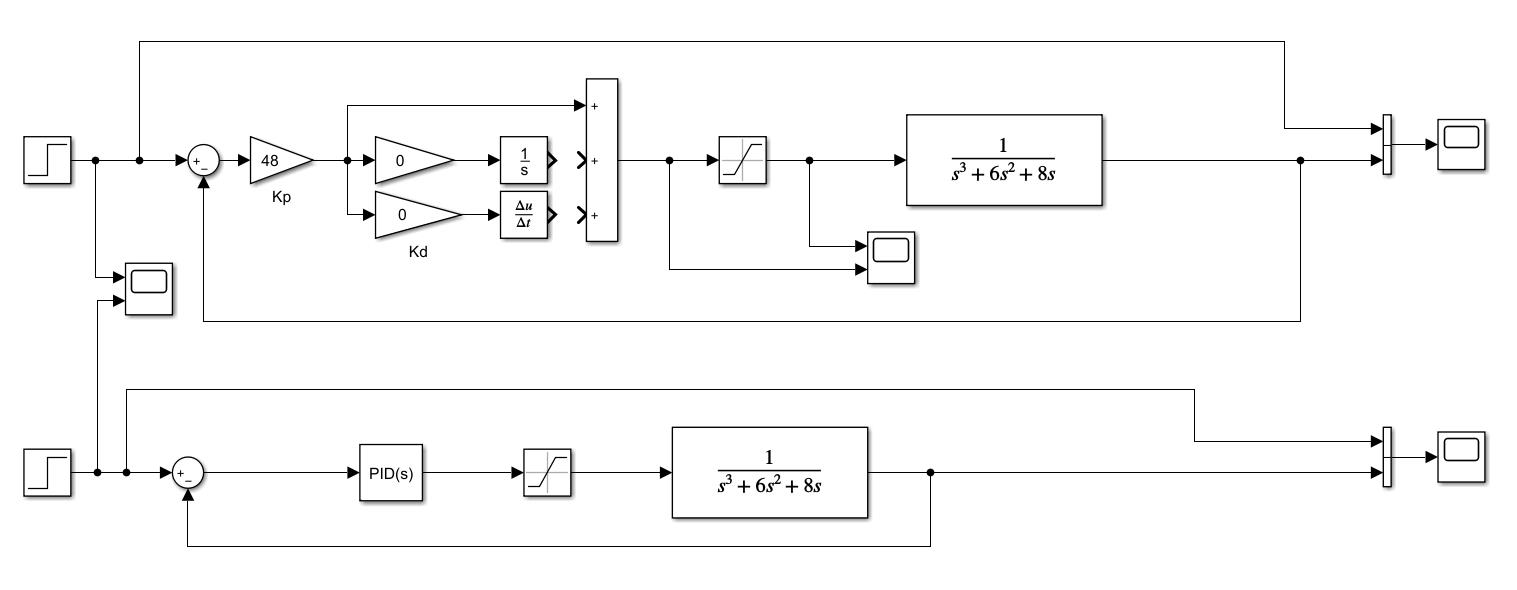
在这里插入图片描述
输入信号：t=1.0 s 由0阶跃上升至5。通过改变kp的值观察输出的波形，最后确定等幅镇荡的临界比例度δk和临界周期Tk。其中，kp = 50，Tk = 11.228 s ，δk = 1/kp = 0.02。

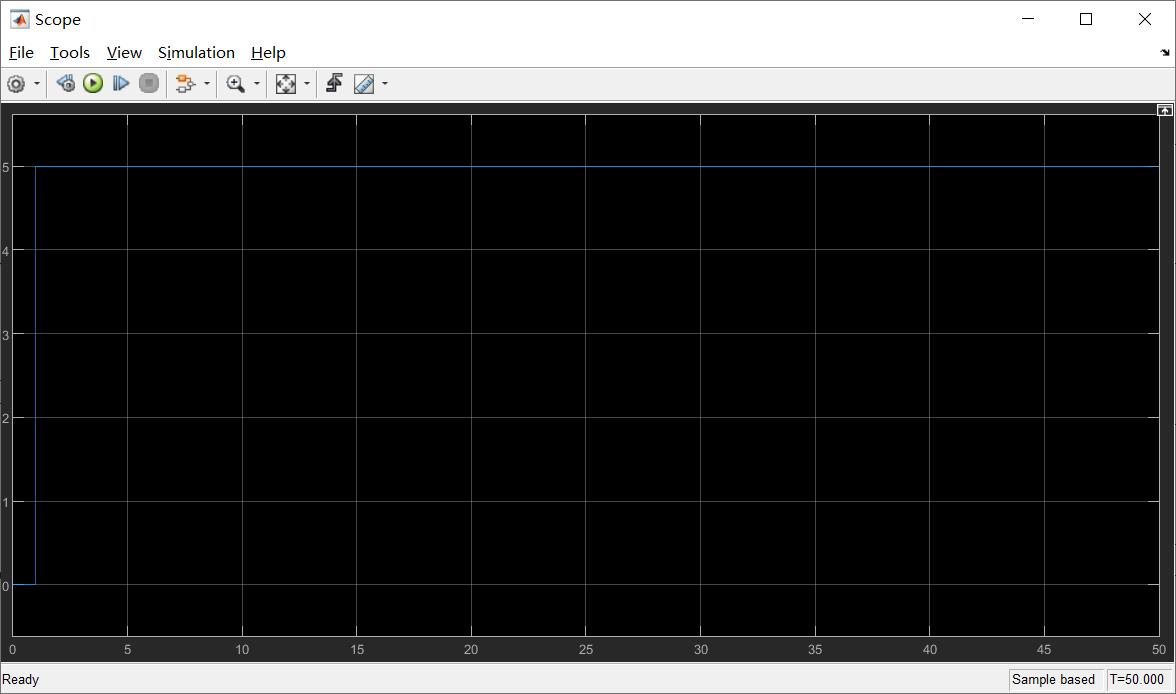
当kp = 1.0时，系统的阶跃响应输出曲线如下：
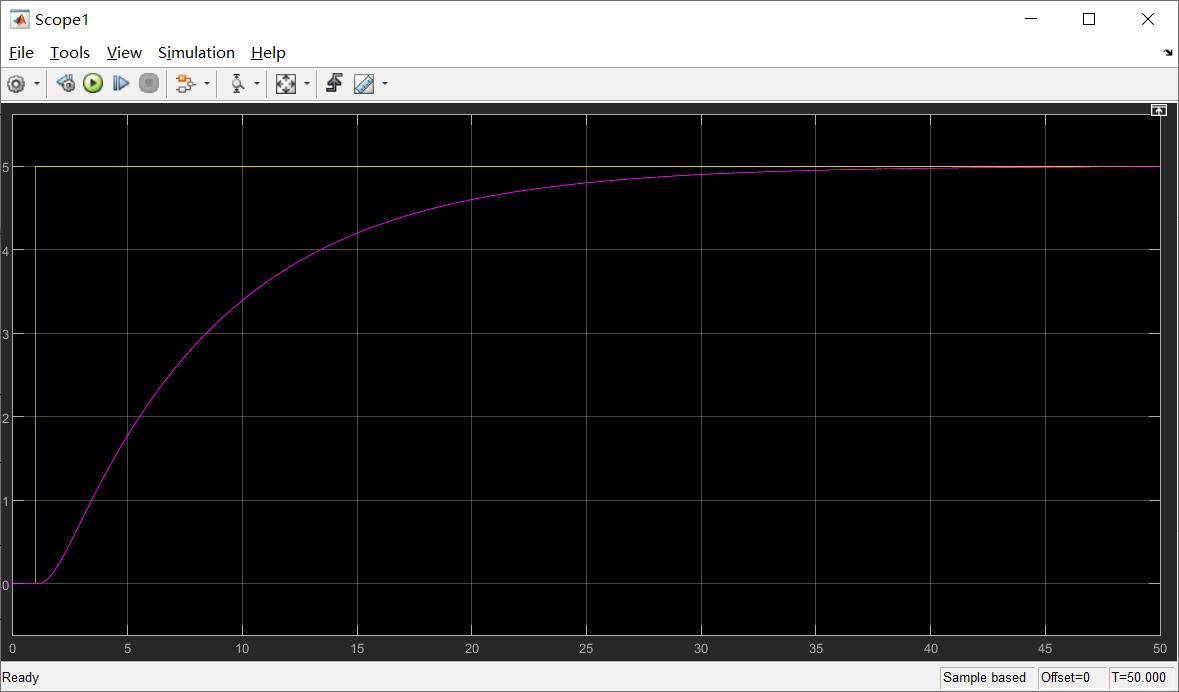
在这里插入图片描述
当kp = 10.0时，系统的阶跃响应输出曲线如下：

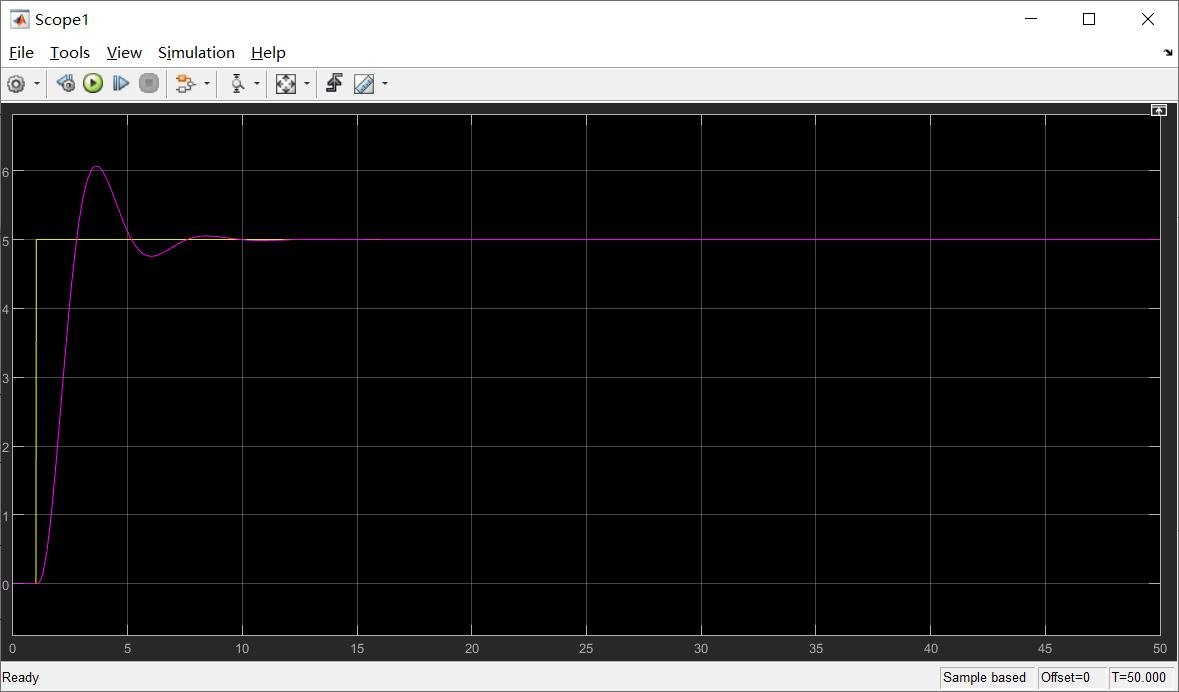
当kp = 30.0时，系统的阶跃响应输出曲线如下：

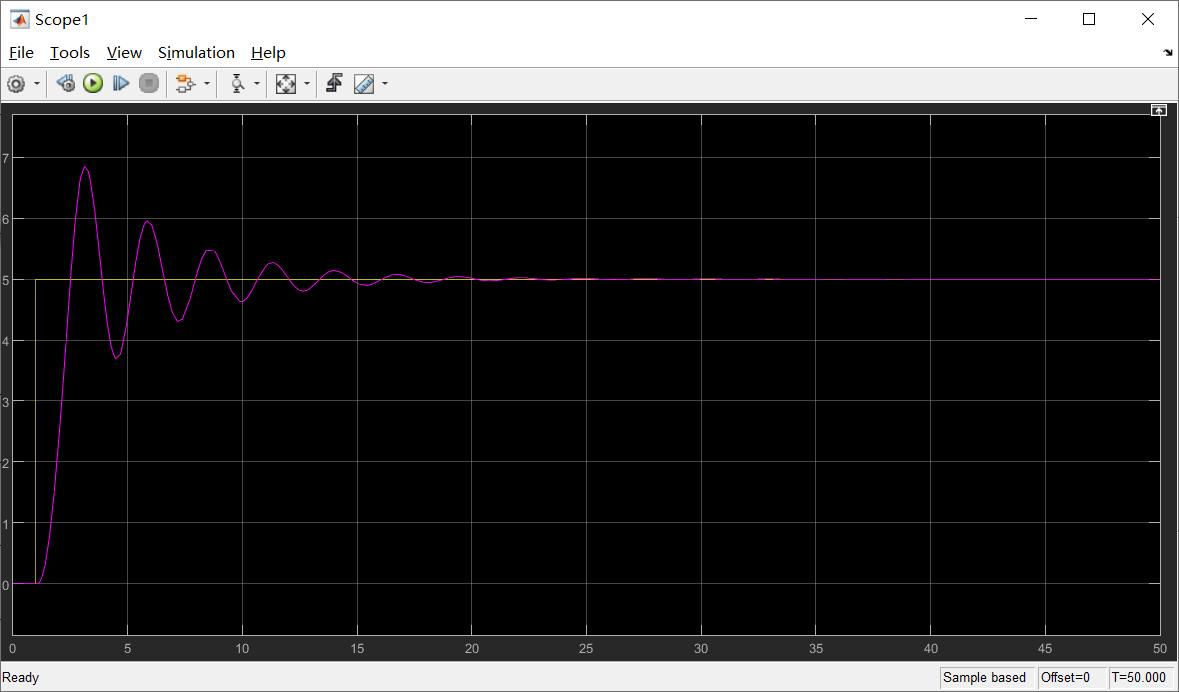
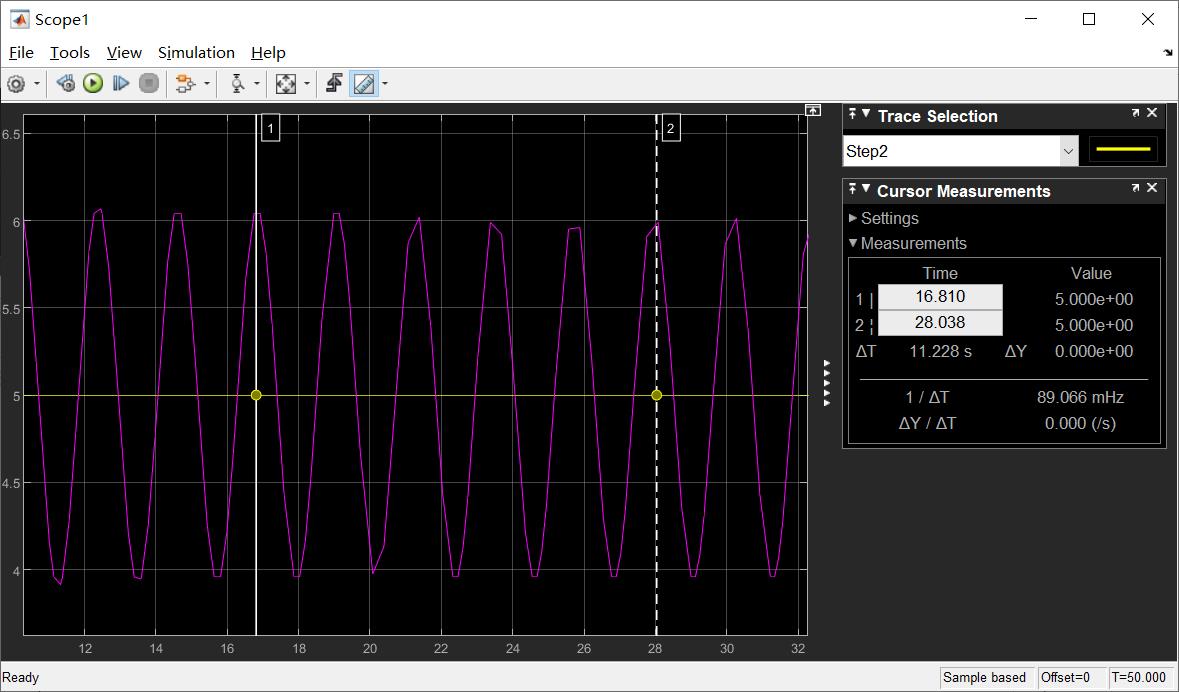
当kp = 50.0时，系统的阶跃响应输出曲线如下：

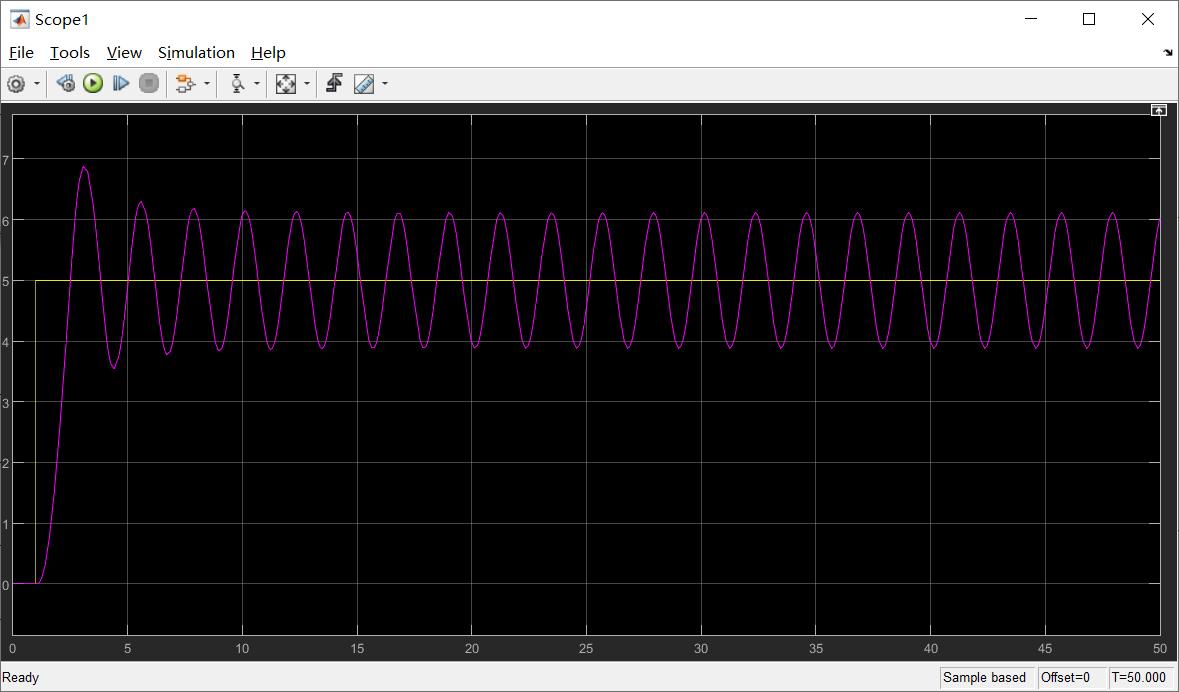
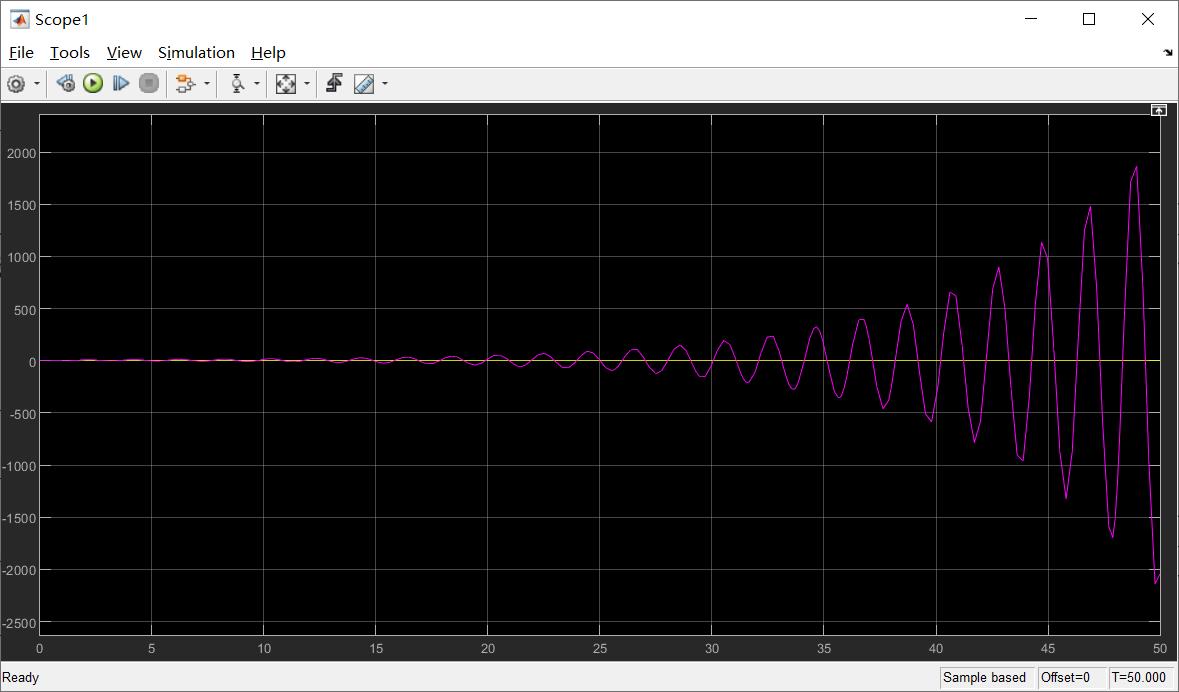
当kp = 60.0时，系统的阶跃响应输出曲线如下：

当kp = 50.0时，系统出现等幅镇荡，可得临界比例度δk和临界周期Tk。其中，kp = 50，Tk = 11.228 s ，δk = 1/kp = 0.02。
在这里插入图片描述
参数整定的计算公式：

$\\begin{array}{l} K_{\\mathrm{p}}=\\frac{1}{\\delta}=\\frac{1}{1.78 \\delta_{\\mathrm{k}}}, \\quad \\delta_{\\mathrm{k}}=\\frac{1}{K_{\\mathrm{p}}^{\\prime}}, K_{\\mathrm{p}}^{\\prime}=50 \\\\ K_{\\mathrm{i}}=K_{\\mathrm{p}} \\frac{T}{T_{\\mathrm{i}}}, \\quad T_{\\mathrm{i}}=0.5 T_{\\mathrm{k}}, \\quad 5 T_{\\mathrm{k}}=11.228, T=10^{-3} \\\\ K_{\\mathrm{D}}=K_{\\mathrm{p}} \\frac{T_{\\mathrm{D}}}{T}, \\quad T_{\\mathrm{D}}=0.125 T_{\\mathrm{k}}, \\quad T_{\\mathrm{k}}=2.2456 \\end{array}$

计算可得PID控制器参数为：

$\\begin{array}{l} K_{\\mathrm{p}}=\\frac{1}{\\delta}=\\frac{1}{1.78 \\delta_{\\mathrm{k}}}=0.011 \\\\ K_{\\mathrm{i}}=K_{\\mathrm{p}} \\frac{T}{T_{\\mathrm{i}}}=0.011 \\times \\frac{1 \\times 10^{-3}}{0.5 \\times 2.2456}=0.000009 \\\\ K_{\\mathrm{D}}=K_{\\mathrm{p}} \\frac{T_{\\mathrm{D}}}{T}=0.011 \\times \\frac{0.125 \\times 2.2456}{1 \\times 10^{-3}}=3.0877 \\end{array}$