实验8 河流流量估计与数据插值

Posted 2021-06-23 从零开始的智障生活

function a=lagrange(x,y) % 输入数据点坐标向量x,y输出插值多项式a
    L=length(x); % 坐标向量对数n，等于要解的多项式系数的个数n，等于系数矩阵的阶数，而多项式则是n-1次多项式，系数矩阵第一列是1
    A=ones(L); % 系数矩阵阶数为n，初始化全为1
    % 系数矩阵第一列是0，然后按列对系数矩阵A赋坐标向量x的值，具体情形参看博客描述
    for j=2:L 
        A(:,j)=A(:,j-1).*x'; % 范德蒙行列式特性，后一列都是前一列乘一个固定向量，向量或矩阵加单引号是共轭转置，因为x元素都是实数，所以共不共轭一样的
    end
    X=inv(A)*y'; % 得出系数向量[a0,a1,...,an-1]
    for i=1:L % 调转系数向量方向，因为polyval要求系数是从高次到低次排
        a(i)=x(L-i+1);
    end

clear;close all;clf;clc;
x=[1,2,3,4,5];
y=[-1,1.5,2.1,3.6,4.9];
hold on;
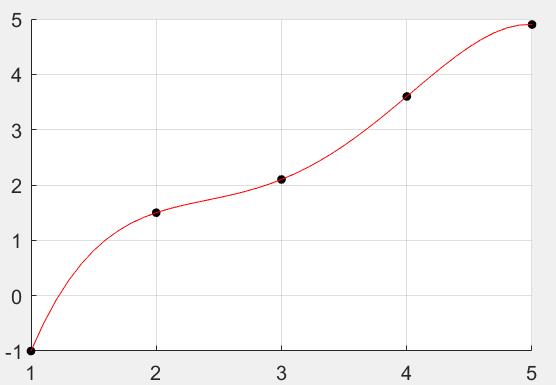
plot(x,y,'k.','markersize',15);
axis([0,5,-1,5]);
grid;
p=lagrange(x,y);
% disp(p);
t=1:0.1:5;
u=polyval(p,t);
plot(t,u,'r-');

clear;close all;clf;clc;
x=-5:0.1:5;
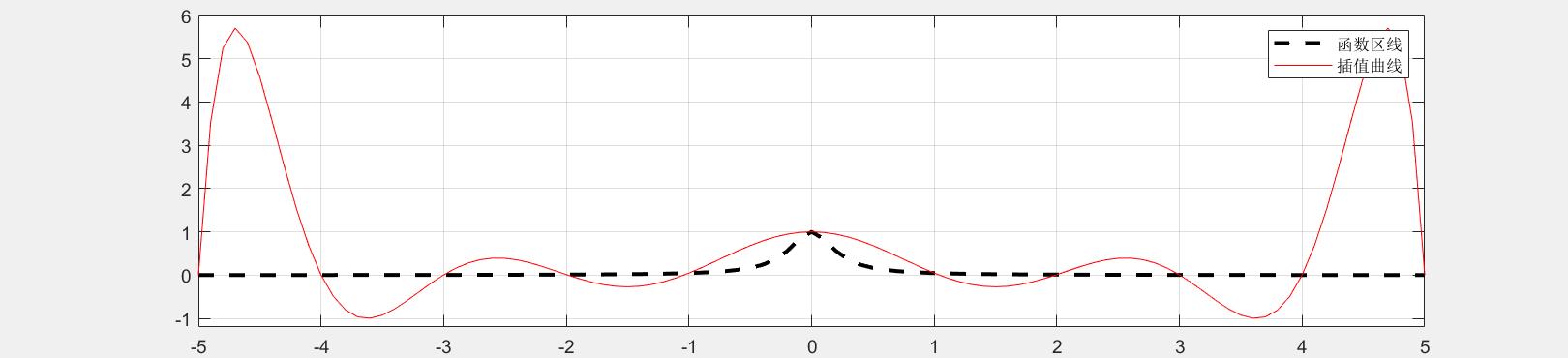
y=1./(1+20*x.*x);
plot(x,y,'k--','linewidth',2);
axis([-5 5 -1.2 6]);
grid;
hold on;
x=-5:5;
y=1./(1+20*x.*x);
p=lagrange(x,y);
t=-5:0.1:5;
f=polyval(p,t);
plot(t,f,'r-');
legend('函数区线','插值曲线');

clear;close all;clf;clc;
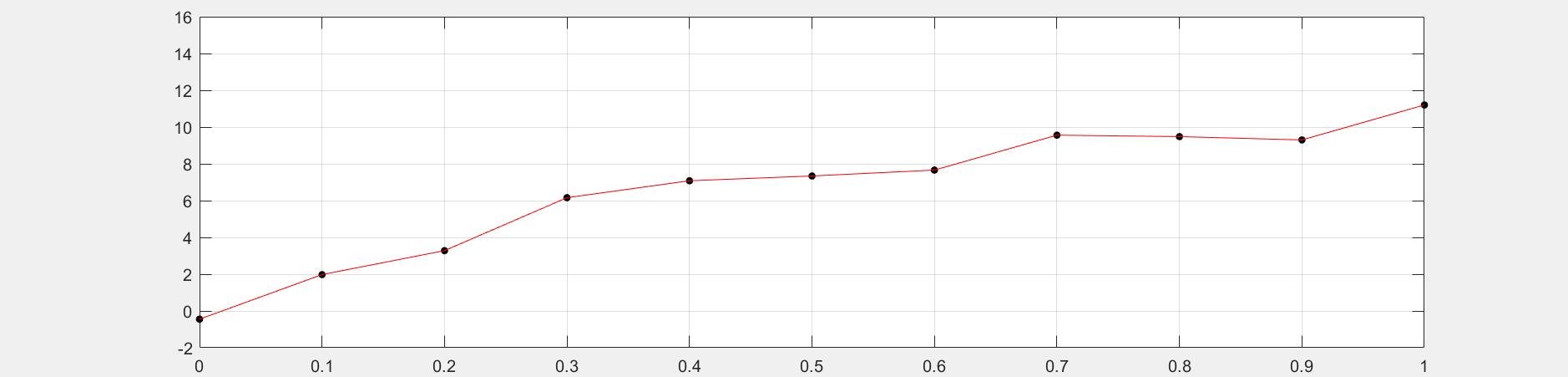
x=0:0.1:1;
y=[-0.447 1.978 3.28 6.16 7.08 7.34 7.66 9.56 9.48 9.3 11.2];
plot(x,y,'k.','markersize',15);
axis([0 1 -2 16]);
grid;
hold on;
t=0:0.01:1;
u=interp1(x,y,t);
plot(t,u,'r-');

clear;close all;clf;clc;
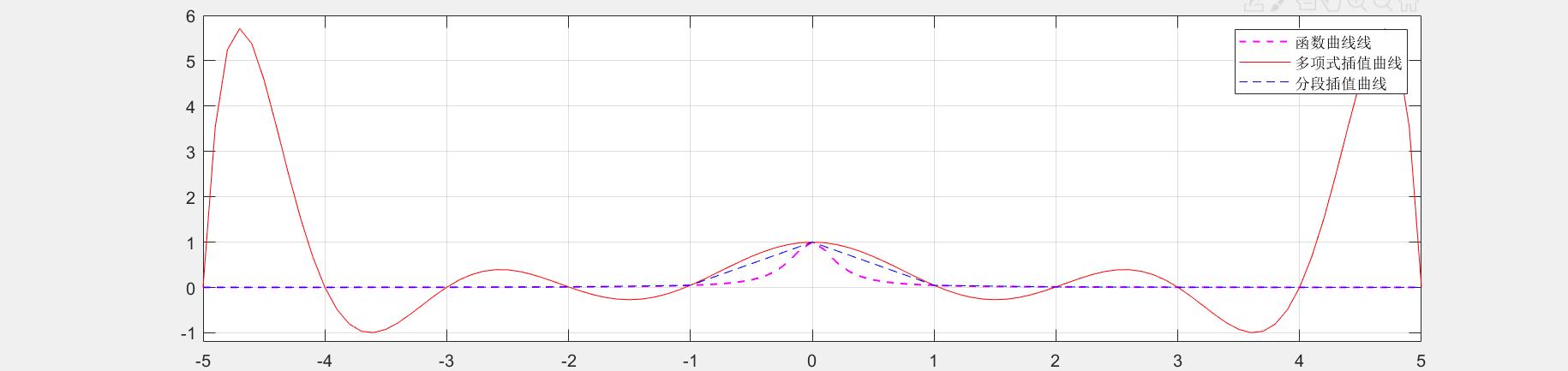
x=-5:0.1:5;
y=1./(1+20*x.*x);
plot(x,y,'m--','linewidth',1);
axis([-5 5 -1.2 6]);
grid;
hold on;
x=-5:5;
y=1./(1+20*x.*x);
p=lagrange(x,y);
t=-5:0.1:5;
f=polyval(p,t); % 多项式插值
plot(t,f,'r-');
u=interp1(x,y,t); % 分段插值
plot(t,u,'b--');
legend('函数曲线线','多项式插值曲线','分段插值曲线');

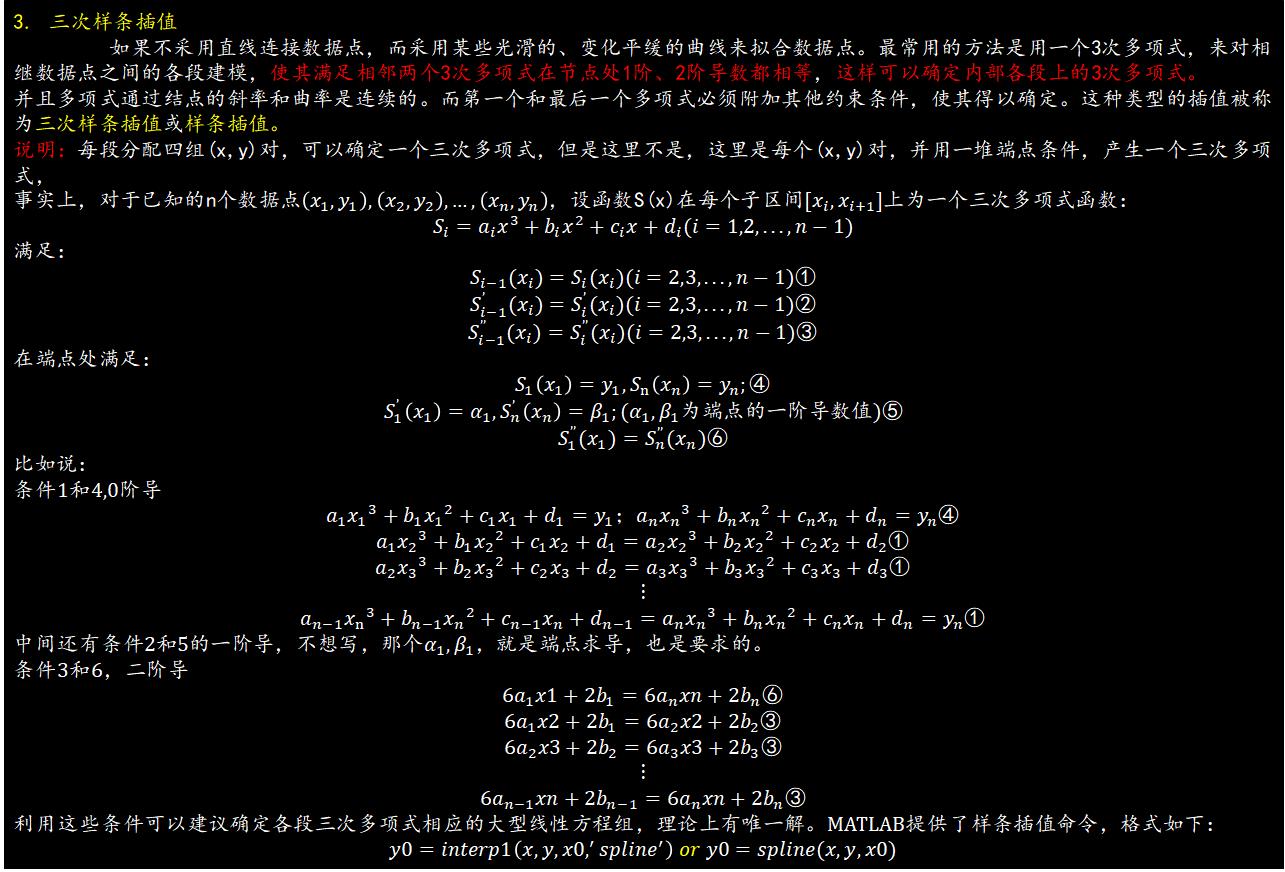
clear;close all;clf;clc;
x=-5:0.1:5;
y=1./(1+20*x.*x);
plot(x,y,'m--','linewidth',1);
axis([-5 5 -1.2 6]);
grid;
hold on;
x=-5:5;
y=1./(1+20*x.*x);
p=lagrange(x,y);
t=-5:0.1:5;
f=polyval(p,t); % 多项式插值
plot(t,f,'r-');
u=interp1(x,y,t); % 分段插值
plot(t,u,'b--');
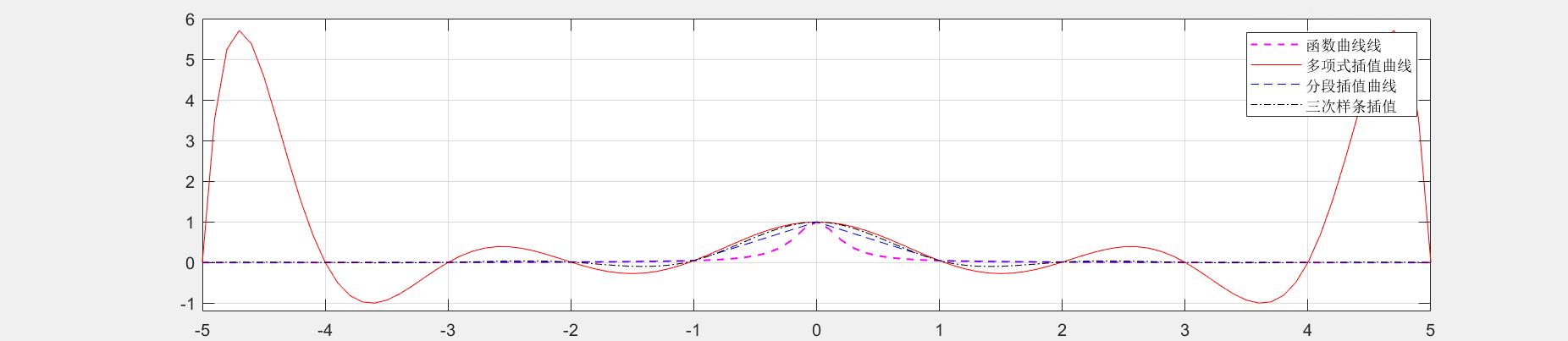
v=interp1(x,y,t,'spline'); % 三次样条插值
plot(t,v,'k-.');
legend('函数曲线线','多项式插值曲线','分段插值曲线','三次样条插值');