文献阅读13期：Deep Learning on Graphs: A Survey - 2
Posted RaZLeon
tags:
篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了文献阅读13期：Deep Learning on Graphs: A Survey - 2相关的知识，希望对你有一定的参考价值。
[ 文献阅读·综述 ] Deep Learning on Graphs: A Survey [1]
推荐理由：图神经网络的survey paper，在很多的领域展现出了独特的作用力，分别通过GRAPH RNN（图循环网络）、GCN（图卷积）、GRAPH AUTOENCODERS（图自编码器）、GRAPH REINFORCEMENT LEARNING（图强化学习模型）、GRAPH ADVERSARIAL METHODS（图对抗模型）等五个类型的模型进行阐述，可以让大家对图神经网络有一个整体的认识
4. 图卷积网络（Graph Convolutional Networks）
- 下表首先展现了一部分GCN的特性：
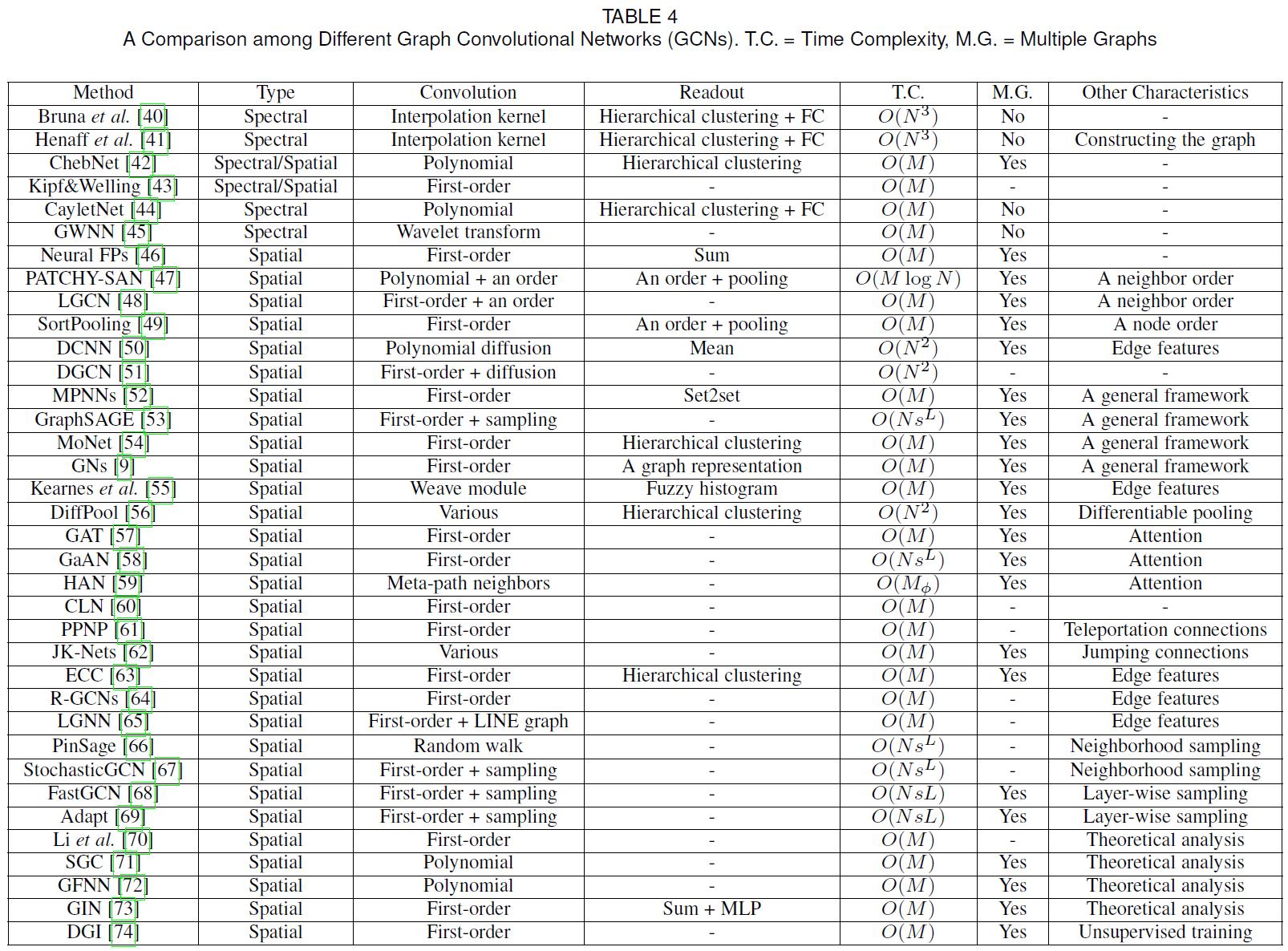
可以看出，目前提出的图卷积网络还是非常丰富的。
4.1.卷积运算
- 卷积运算在CNNs中非常常见，但它并不能直接应用在图网络当中，因为图网络没有Grid结构。
4.1.1.谱方法
- 图拉普拉斯矩阵被引入，它的功能类似于信号处理中的傅里叶基，图的卷积操作
∗
G
* G
∗G，可以定义为如下形式：
u 1 ∗ G u 2 = Q ( ( Q T u 1 ) ⊙ ( Q T u 2 ) ) (5) \\mathbf{u}_{1} *_{G} \\mathbf{u}_{2}=\\mathbf{Q}\\left(\\left(\\mathbf{Q}^{T} \\mathbf{u}_{1}\\right) \\odot\\left(\\mathbf{Q}^{T} \\mathbf{u}_{2}\\right)\\right)\\tag{5} u1∗Gu2=Q((QTu1)⊙(QTu2))(5)
其中 u 1 , u 2 ∈ R N \\mathbf{u}_{1}, \\mathbf{u}_{2} \\in \\mathbb{R}^{N} u1,u2∈RN是两种定义在节点上的信号， Q \\mathrm{Q} Q是 L \\mathrm{L} L的特征向量。 - 通过和 Q T \\mathbf{Q}^{T} QT相乘，即可将图信号 u 1 , u 2 \\mathbf{u}_{1}, \\mathbf{u}_{2} u1,u2转换到谱域当中。而与 Q \\mathbf{Q} Q相乘，则是实施逆运算。
- 通过转换后输出信号可以表示为：
u ′ = Q Θ Q T u (6) \\mathbf{u}^{\\prime}=\\mathbf{Q} \\Theta \\mathbf{Q}^{T} \\mathbf{u}\\tag{6} u′=QΘQTu(6)
其中， Θ = Θ ( Λ ) ∈ R N × N \\boldsymbol{\\Theta}=\\boldsymbol{\\Theta}(\\boldsymbol{\\Lambda}) \\in \\mathbb{R}^{N \\times N} Θ=Θ(Λ)∈RN×N是一个可训练filters的对角阵， Λ \\boldsymbol{\\Lambda} Λ是 L \\mathrm{L} L的特征值。 - 一个卷积层可以对不同的输入输出对施加不同的filters：
u j l + 1 = ρ ( ∑ i = 1 f l Q Θ i , j l Q T u i l ) j = 1 , … , f l + 1 (7) \\mathbf{u}_{j}^{l+1}=\\rho\\left(\\sum_{i=1}^{f_{l}} \\mathbf{Q} \\Theta_{i, j}^{l} \\mathbf{Q}^{T} \\mathbf{u}_{i}^{l}\\right) j=1, \\ldots, f_{l+1}\\tag{7} ujl+1=ρ(i=1∑flQΘi,jlQTuil)j=1,…,fl+1(7) - 一般而言，谱域中的filters并不会局限于空间领域，这就意味着在图卷积网络中，每个点有可能被其他所有店影响，而不是仅仅被一小片区域中的点影响。
- 为了解决这个问题，smoothing filters被引入：
diag ( Θ i , j l ) = K α l , i , j (8) \\operatorname{diag}\\left(\\Theta_{i, j}^{l}\\right)=\\mathcal{K} \\alpha_{l, i, j}\\tag{8} diag(Θi,jl)=Kαl,i,j(8)
其中， K \\mathcal{K} K是固定插值核， α l , i , j \\alpha_{l, i, j} αl,i,j是可训练插值系数。 - 然而，有两个根本性问题还未解决：
- 在每步计算的时候，拉普拉斯矩阵的全特征向量都是必须的，每一步前/反向传播所需要的时间复杂度至少是 O ( N 2 ) O\\left(N^{2}\\right) O(N2)，对大规模图网络中，运算量极大
- 因为filter依赖图的特征基 Q \\mathrm{Q} Q，对于不同结构和尺寸的图来说，分享参数几乎是不可能的事情。
4.1.2.运算效率
- 为了解决效率问题，ChebNet被踢出，并且使用了多项式滤波器：
Θ ( Λ ) = ∑ k = 0 K θ k Λ k (9) \\Theta(\\Lambda)=\\sum_{k=0}^{K} \\theta_{k} \\Lambda^{k}\\tag{9} Θ(Λ)=k=0∑KθkΛk(9)
其中， θ 0 , … , θ K \\theta_{0}, \\ldots, \\theta_{K} θ0,…,θK是科学系参数， K K K是多项式阶。ChebNet用切比雪夫展开代替了特征分解：
Θ ( Λ ) = ∑ k = 0 K θ k T k ( Λ ~ ) (10) \\boldsymbol{\\Theta}(\\boldsymbol{\\Lambda})=\\sum_{k=0}^{K} \\theta_{k} \\mathcal{T}_{k}(\\tilde{\\boldsymbol{\\Lambda}})\\tag{10} Θ(Λ)=k=0∑KθkTk(Λ~)(10)
其中， Λ ~ = 2 Λ / λ max − I \\tilde{\\mathbf{\\Lambda}}=2 \\boldsymbol{\\Lambda} / \\lambda_{\\max }-\\mathbf{I} Λ~=2Λ/λmax−I为经过缩放的特征值， λ max \\lambda_{\\max } λmax是最大特征值， I ∈ R N × N \\mathbf{I} \\in \\mathbb{R}^{N \\times N} I∈RN×N为单位阵， T k ( x ) \\mathcal{T}_{k}(x) Tk(x)为k阶切比雪夫多项式，其正交基的rescaling是必要的。 - 利用拉普拉斯矩阵的多项式作为其特征值的多项式，则有
L
k
=
Q
Λ
k
Q
T
\\mathbf{L}^{k}=\\mathbf{Q} \\mathbf{\\Lambda}^{k} \\mathbf{Q}^{T}
Lk=QΛkQT，式6的filter操作可写为如下形式：
u ′ = Q Θ ( Λ ) Q T u = ∑ k = 0 K θ k Q以上是关于文献阅读13期：Deep Learning on Graphs: A Survey - 2的主要内容，如果未能解决你的问题，请参考以下文章
文献阅读17期：Deep Learning on Graphs: A Survey - 6
文献阅读16期：Deep Learning on Graphs: A Survey - 5
文献阅读12期：Deep Learning on Graphs: A Survey - 1
文献阅读17期：Deep Learning on Graphs: A Survey - 6