文献阅读14期：Deep Learning on Graphs: A Survey - 3

Posted 2021-06-23 RaZLeon

[ 文献阅读·综述 ] Deep Learning on Graphs: A Survey [1]

推荐理由：图神经网络的survey paper，在很多的领域展现出了独特的作用力，分别通过GRAPH RNN（图循环网络）、GCN（图卷积）、GRAPH AUTOENCODERS（图自编码器）、GRAPH REINFORCEMENT LEARNING（图强化学习模型）、GRAPH ADVERSARIAL METHODS（图对抗模型）等五个类型的模型进行阐述，可以让大家对图神经网络有一个整体的认识。

4.2.读出操作

• 在使用图卷积操作时，有用的节点特征可以被用来训练求解许多专注于点的任务。而对于专注于图的任务来说，所有点的信息需要被总结成图的级别才行。
• 将这些点信息总结起来的过程，被称为读出操作（Readout Operations）。
• 基于度和本地近邻，标准的CNNs通过踱步跨度卷积或是池化来逐步降低分辨率。
• 由于图网络不是grid结构，这些已有的方法不能被直接使用。
• 序不变性：对于图网络来说，读出操作有个很关键的地方就在于，读取节点的顺序是不能够改变的。如用双射函数改变点和边的indices，那也不能改变整个图的表达。
• 有时候结构上不同的两个图，也有可能有同样的表达方式。

4.2.1.统计学

• 简单的order-invariant操作有很多，但大多都是统计学里的知识比如求和、求平均或是最大池化等等，比如：
  $${\mathbf{h}}_G=\sum _{i=1}^N{\mathbf{h}}_i^L\text{ or }{\mathbf{h}}_G=\frac{1}{N}\sum _{i=1}^N{\mathbf{h}}_i^L\text{ or }{\mathbf{h}}_G=\max \left\{{\mathbf{h}}_i^L,\forall i\right\}\text{\hspace{1em}(28)}$$
  其中${\mathbf{h}}_G$为整个图G的表达，${\mathbf{h}}_i^L$则代表了L层的具体节点i
• 不过很显然的是，这种基础的统计学方法很难将整个图表达好，信息损失极大。
• Kearnes等人提出一种模糊直方图方法，通过计算每个节点对这些直方线的隶属度。

这种方法可以用来区分有相同sum/average/maximum，但有不同分布的网络。

• 另一种常见方法是增加最后一层全连层：
  $${\mathbf{h}}_G=\rho \left(\left[{\mathbf{H}}^L\right]{\Theta }_{FC}\right)\text{\hspace{1em}(29)}$$

4.2.2.层次聚类

• 除去可以一分为二的点和图级结构，图本身可以有极为丰富的层次结构，这种结构可以经由层次聚类处理，挖掘出很多丰富的信息。
  
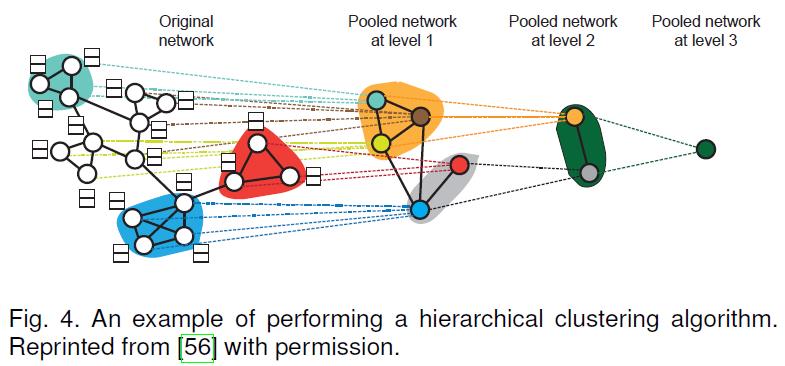
• 上图就展示了一种节点的密度聚类。
• 对ChebNet和MoNet也有采用一种以贪婪等级聚类的方法，同一时间可以融合两个节点，而且能够通过迅速池化来将节点排列进平衡二叉树。ECC采用一种自分解方法来实施层次聚类。
• 但上述层次聚类方法基本独立于图卷积，他们都只是一种预处理步骤，不能实现端到端训练。
• 为解决这一问题，一种结合了图卷积的层次聚类算法被提出，作者提出一种用隐式表达的软聚类，并将其实施在每一层当中：
  $${\mathbf{S}}^l=\mathcal{F}\left({\mathbf{A}}^l,{\mathbf{H}}^l\right)\text{\hspace{1em}(30)}$$
• 提取后的图可以被表述为：
  $${\mathbf{H}}^{l+1}={\left({\mathbf{S}}^l\right)}^T{\hat{\mathbf{H}}}^{l+1},{\mathbf{A}}^{l+1}={\left({\mathbf{S}}^l\right)}^T{\mathbf{A}}^l{\mathbf{S}}^l\text{\hspace{1em}(31)}$$

4.2.3.附加排序和其他

• 如何为节点组件一个更好的排序是一个持续性研究方向，论文作者有另一篇综述，详情请看原文。

4.2.4.小结

• 简而言之，最简单的统计学方法能做readout，但直方聚类算法结合图卷积可以获得更多优势，而且技术也相对成熟。其它算法比如加入伪节点或者，强加顺序的方法也都有被开发出来。

参考文献

[1] Zhang Z, Cui P, Zhu W. Deep learning on graphs: A survey[J]. IEEE Transactions on Knowledge and Data Engineering, 2020.