一篇文章带你搞懂回溯(万字:核心思维+图解+习题+题解思路+代码注释)
Posted 深林无鹿
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了一篇文章带你搞懂回溯(万字:核心思维+图解+习题+题解思路+代码注释)相关的知识,希望对你有一定的参考价值。
认真看完本篇文章你将精通掌握关于回溯的以下几点:
回溯的本质是什么?
如何轻松的写出回溯的代码?
如何一眼看穿题目可以用回溯求解?
如何通过startIndex进行去重、剪枝?
什么是回溯中去重等级?
如何利用扫描方向进行合理剪枝?
最好搭配课后练习学习,每道题都有详细的题解,以及本人做题时候一步一步思考的过程,附上了详细的代码注释。既深究于细节、又放眼全局,相信你一定有所收获!!
文章有点长可以先收藏哦~
一、回溯介绍
1、什么是回溯
回溯算法实际上一个类似枚举的搜索尝试过程,主要是在搜索尝试过程中寻找问题的解,当发现已不满足求解条件时,就“回溯”返回,尝试别的路径。
2、回溯思想和本质的分析
根据回溯的定义可以知道,回溯的问题,本质上就是决策树的遍历。不断地做决策,然后取消做过的决策进行试错。是一种暴力的遍历方法。可以总结出一套比较固定的思维模板:
- 路径:已经做出的选择。
- 选择列表:当前状态可以选择的状态列表。
- 结束条件:到达决策树底层,无法再做出决策。
回溯的关键代码就是在选择列表中的递归思路。
模板代码:
void trackback(选择列表,路径) {
if (满足结束条件){
result.add(路径);
return;
}
for (选择: 选择列表) {
做决策;
trackback(做完决策后的选择列表,路径);
撤销决策;
}
}
我们从代码中发现,在选择列表中做决策的位置,明明对应的就是树的遍历:
- 做决策 -> 前序遍历
- 撤销决策 -> 后序遍历
我们画图来理解一下:
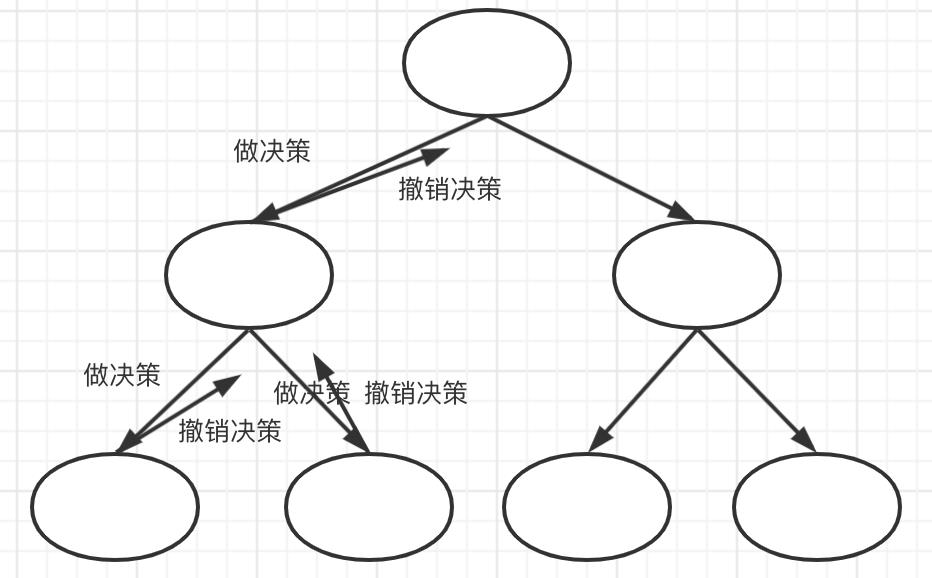
就很形象的看出来回溯的本质了,在后面刷题巩固的时候只需要牢牢把握它的本质,就可以游刃有余的处理复杂的回溯问题。
核心思路确定了,问题基本就解决了,其他细枝末节的地方,以及优化思路会在后面的练习中进行细致的讲解。
二、配套练习:
1、组合类问题
leetcode 77. 组合
题目难度:中等

解题思路:
根据题意,输出[1, n]的组合,可以建立递归过程,在每次递归回溯的时候,调整扫描范围的起点。
根据回溯算法的模板,写出关键伪代码:
void backtrack(int n, int k, int startIndex) {
if(路径大小 == k) {
ans.add(path);
}
for(int i = startIndex; i <= n; i ++) {
// TODO 选择
backtrack(n, k, i + 1);
// TODO 撤销选择
}
}
代码补全后的结果如下:
class Solution {
private List<List<Integer>> ans = new ArrayList<>();
private Deque<Integer> path = new LinkedList<>();
public List<List<Integer>> combine(int n, int k) {
backtrack(n, k, 1);
return ans;
}
public void backtrack(int n, int k, int startIndex) {
if (path.size() == k) {
ans.add(new ArrayList<>(path));
return;
}
for (int i = startIndex; i <= n; i ++) {
path.add(i);
backtrack(n, k, i + 1);
path.removeLast();
}
}
}
我们在走完整个流程后,消耗的时间十分之长在leetcode上用时25ms,在仔细分析后不难发现,我们这个回溯的过程中有很多无效回溯,可以进行剪枝:
剪枝核心:在循环中横向遍历树的时候,如果得知后面的元素个数无法达到要求的k个,就不必在进行递归回溯了。这个可以通过控制变量i的范围来达到目的,分析过程:
- 路径即为已选择的元素个数 ->
path.size() - 后续的过程还需要的元素个数 ->
k - path.size() i在区间[startIndex,n]中可以优化为[startIndex,n - (k - path.size())]和[n - (k - path.size()) + 1,n],其中后面的区间因为选择后无法满足k个元素个数要求,可以舍去
举个例子图解分析:
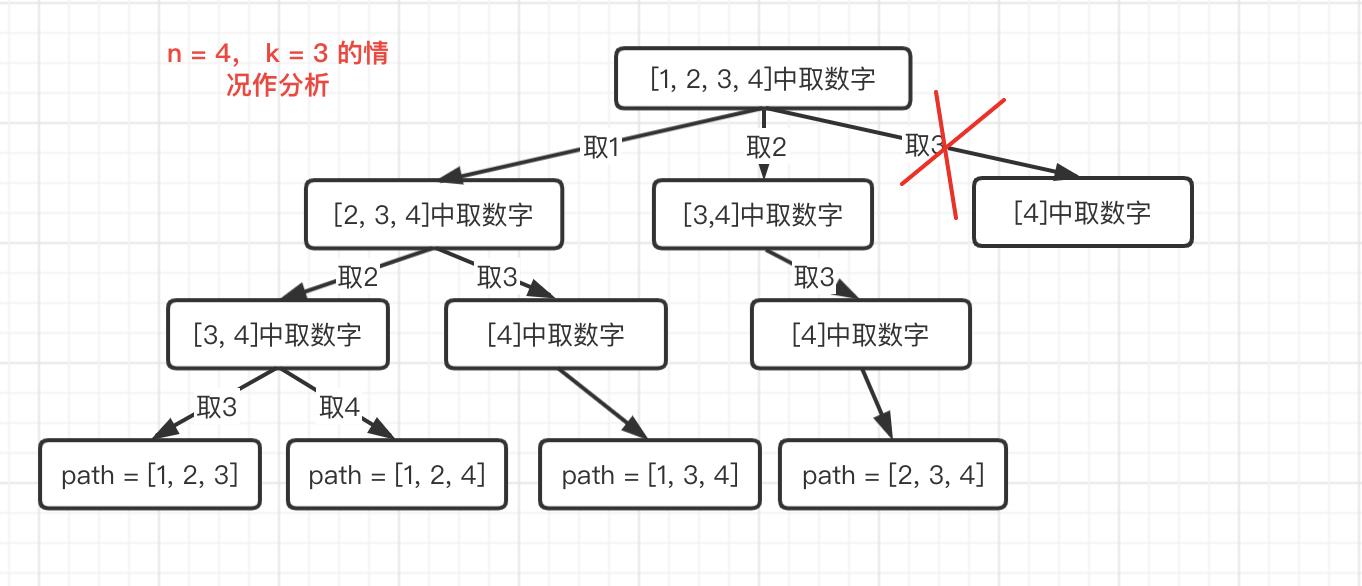
可以知道,k越大后面剪掉的部分越多。
另i的起点不能超过 n - (k - path.size()) + 1 这个就是i的最大起点,在大之后,path的个数就无法满足k个了。
剪枝后的代码:
class Solution {
private List<List<Integer>> ans = new ArrayList<>();
private Deque<Integer> path = new LinkedList<>();
public List<List<Integer>> combine(int n, int k) {
backtrack(n, k, 1);
return ans;
}
public void backtrack(int n, int k, int startIndex) {
if (path.size() == k) {
ans.add(new ArrayList<>(path));
return;
}
// 剪支优化
for (int i = startIndex; i <= n - (k - path.size()) + 1; i ++) {
path.add(i);
backtrack(n, k, i + 1);
path.removeLast();
}
}
}
leetcode 216. 组合总和 III
题目难度:中等

解题思路:
和上一道题思路基本一样,不一致的地方有两点
- 结束条件不一致:如果路径个数达到
k,满不满足条件都退出。- 回溯逻辑不同,每决策一次后,更新
sum,在本题中采用的是将n进行更新来实现的。其他部分同上一题基本一致,这里给出代码,并做了详细注释。
public void backtrack(int k, int n, int startIndex) {
// 满足结束条件,满足题目条件,加入结果集返回
if (path.size() == k && n == 0) {
res.add(new ArrayList<>(path));
return;
// 满足结束条件,不满足题目条件,直接返回
} else if (path.size() == k && n != 0) {
return;
}
// 这里注意循环上线不能超过9,题目表明数字要求在1-9之间
for (int i = startIndex; i <= 9; i ++) {
path.add(i);
// 更新 n 为 n - i 用于 判断结束时是否满足题目条件
backtrack(k, n - i, i + 1);
path.removeLast();
}
}
这道题依然可以进行剪枝操作,并且操作十分简单:
在进入递归的是否提前判断,如果n已经小于0了,直接返回即可。
public void backtrack(int k, int n, int startIndex) {
// 剪枝操作
if (n < 0) return;
if (path.size() == k && n == 0) {
res.add(new ArrayList<>(path));
return;
} else if (path.size() == k && n != 0) {
return;
}
for (int i = startIndex; i <= 9; i ++) {
path.add(i);
backtrack(k, n - i, i + 1);
path.removeLast();
}
}
leetcode 39. 组合总和
题目难度:中等

解题思路:
这道题和第二题思路基本一致,只不过在回溯的时候不需要对
startIndex进行+1
public void backtrack(int[] candidates, int target, int startIndex) {
if (target < 0) {
return;
}
if (target == 0) {
res.add(new LinkedList<>(path));
return;
}
for (int i = startIndex; i < candidates.length; i ++) {
path.add(candidates[i]);
// startIndex 不需要加1
backtrack(candidates, target - candidates[i], i);
path.removeLast();
}
}
leetcode 40. 组合总和 II
题目难度:中等

解题思路:
这道题和上面不同的点在于,不允许出现同样的解,表明在确定树的宽度的时候需要根据
candidates[i]的值对i的自增进行修正,避免后续决策树建立的时候出现相同解。
public void backtrack(int[] candidates, int target, int startIndex) {
if (target < 0) {
return;
}
if (target == 0) {
res.add(new ArrayList<>(path));
return;
}
// && 后面的逻辑用来剪枝
for (int i = startIndex; i < candidates.length && target - candidates[i] >= 0; i ++) {
path.add(candidates[i]);
backtrack(candidates, target - candidates[i], i + 1);
path.removeLast();
// 修正i ,避免后续决策树建立的时候出现相同解
while (i < candidates.length - 1 && candidates[i] == candidates[i + 1]) i ++;
}
}
leetcode 17. 电话号码的字母组合
题目难度:中等
解题思路:
思考步骤
- 首先我们根据题意确定path:用
StringBuffer来存储- 然后确定结束条件:
sb.length() == digits.length()- 确定关键递归逻辑:代码星标处位置
把回溯问题的核心关键点把握住,同时确定决策树的构造:
- 选择列表决定树的宽度
- 问题要求长度决定树的深度
这道题的第二关键点是:选择列表与决策位置
i是相关联的
class Solution {
private List<String> res = new ArrayList<>();
private StringBuffer sb = new StringBuffer();
private String[] dict = {"","abc", "def", "ghi", "jkl", "mno", "pqrs", "tuv", "wxyz"};
// private Map<String, String> dict = new HashMap<>();
public List<String> letterCombinations(String digits) {
if (digits.length() == 0) return res;
backtrack(digits, 0);
return res;
}
void backtrack(String digits, int index) {
if(sb.length() == digits.length()) {
res.add(sb.toString());
return;
}
char num = digits.charAt(index);
String letters = dict[num - '1'];
// ***************关键逻辑*********************
for (int i = 0; i < letters.length(); i ++) {
sb.append(letters.charAt(i));
backtrack(digits, index + 1);
sb.deleteCharAt(sb.length() - 1);
}
}
}
2、分割字符串类
leetcode 131. 分割回文串
题目难度:中等

解题思路:
明确题意:
简单化分析: 分割字符串可以看做用一把刀在遍历的时候随机切开,最后判断是否满足条件。
分析: 遍历的每一步,都可以分为切和不切。这时候问题就可以转化为决策的问题了,触及决策问题,我们就可以用回溯的方法去解决。
切与不切的标准: 切割后是否满足条件,满足条件则递归下去,继续切直到满足条件,否则跳过这次无法完成目标的决策。
详细见代码分析
class Solution {
private List<List<String>> res = new ArrayList<>();
private Deque<String> path = new LinkedList<>();
public List<List<String>> partition(String s) {
backtrack(s, 0);
return res;
}
// 不可以回头反复切割,需要通过startIndex控制每一层+1
// 确保每次只切割后面的串
public void backtrack(String s, int startIndex) {
// 如果切刀到达字符串尾端,说明存在满足条件的path,加入结果集返回
if (startIndex >= s.length()) {
res.add(new ArrayList<>(path));
return;
}
for (int i = startIndex; i < s.length(); i ++) {
// 如果切刀起点与后面的i控制的字符串之间的字符串为回文
// 就切割,并进行继续回溯,否则跳出
if(isPalindrome(s, startIndex, i)) {
path.add(s.substring(startIndex, i + 1));
} else continue;
backtrack(s, i + 1);
path.removeLast();
}
}
// 判断是否回文
public boolean isPalindrome(String s, int startIndex, int end) {
for (int i = startIndex, j = end; i < j; i ++, j --) {
if (s.charAt(i) != s.charAt(j)) return false;
}
return true;
}
}
leetcode 93. 复原 IP 地址
题目难度:中等
解题思路:
切割类题目同上一道题一样,思考步骤:
结束条件:s中'.'的个数有三个了,就进行返回。
回溯逻辑: 在字符串s上进行切割,在切割时,判断截取的字符串是否满足IP地址的格式,满足条件则继续 切割 + 回溯切,不满足条件则跳出循环。
详细见代码分析
class Solution {
private List<String> res = new ArrayList<>();
public List<String> restoreIpAddresses(String s) {
if (s.length() > 12) return res;
backtrack(s, 0, 0);
return res;
}
public void backtrack(String s, int startIndex, int dotNumber) {
// 结束条件
if (dotNumber == 3) {
// 同时满足第四段数字满足IP地址格式时,加入结果集
if (isValidIp