Coding for Quantum Computing: Creating an Adder Circuit

Posted 2021-06-22 安徽思远

Quantum Addtion

Adder Circuit satisfies tradtional binary addition operation.

A	B	result
0	0	00
0	1	01
1	0	01
1	1	10

这里需要根据Quantum Computing的特点设计一个Circuit满足如上的加法运算。

在该Circuit中，A和B量子位作为输入，result通过两个measurement输出。

Entanglement

这里我们需要借助entanglement来实现这个结果。首先我们来看一下CNOT Gate，其实是XOR Gate。


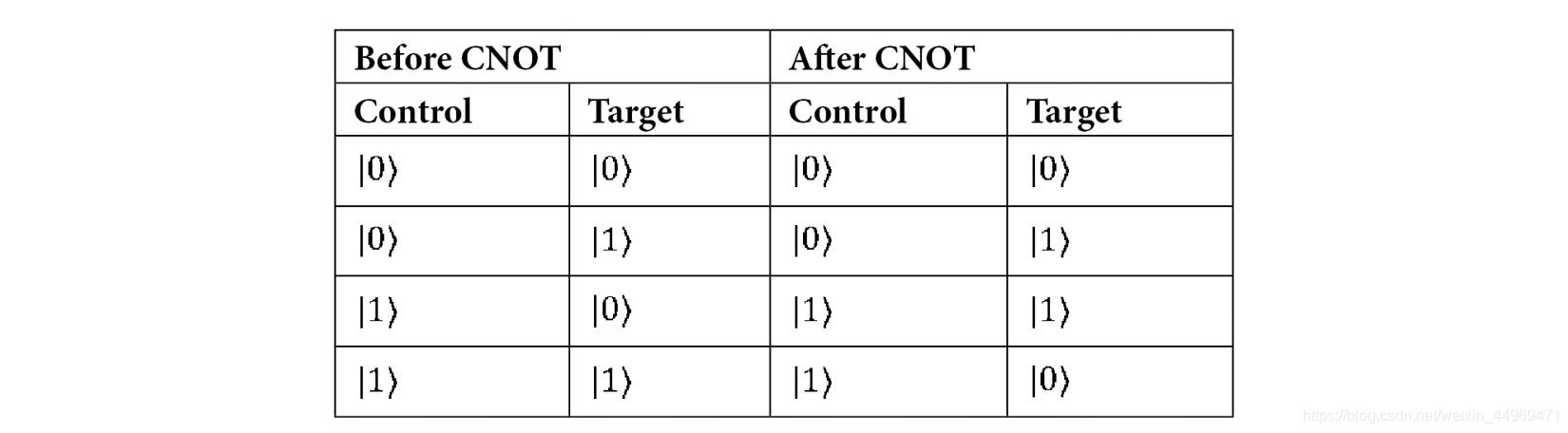
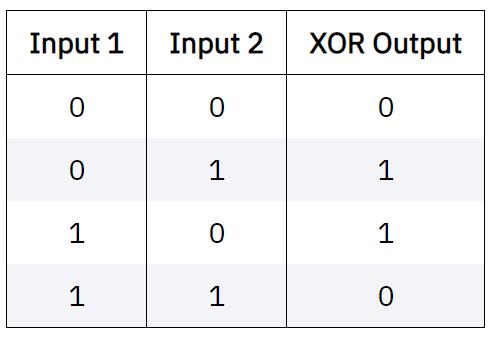
XOR Gate满足加法运算中第一个bit位的要求。

接下来对于第二个bit位，不难发现是一个AND Gate。

For this, we need a new gate: like a CNOT but controlled on two qubits instead of just one. This will perform a NOT on the target qubit only when both controls are in state 1. This new gate is called the Toffoli. For those of you who are familiar with Boolean logic gates, it is basically an AND gate.

Coding

qc_ha = QuantumCircuit(4,2)
# encode inputs in qubits 0 and 1
qc_ha.x(0) # For a=0, remove the this line. For a=1, leave it.
qc_ha.x(1) # For b=0, remove the this line. For b=1, leave it.
qc_ha.barrier()
# use cnots to write the XOR of the inputs on qubit 2
qc_ha.cx(0,2)
qc_ha.cx(1,2)
# use ccx to write the AND of the inputs on qubit 3
qc_ha.ccx(0,1,3)
qc_ha.barrier()
# extract outputs
qc_ha.measure(2,0) # extract XOR value
qc_ha.measure(3,1) # extract AND value

qc_ha.draw()

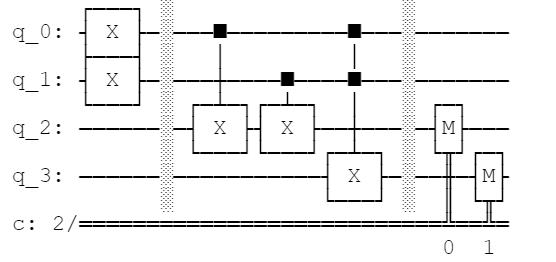
然后我们对结果进行测量，就可以实现classical computing中的加法运算了。注意这里q_0和q_1无论取值为0还是1，都满足加法运算的规则。