剑指 Offer 07. 重建二叉树千字分析，三种方法

Posted 2021-06-22 来老铁干了这碗代码

立志用最少的代码做最高效的表达

---

输入某二叉树的前序遍历和中序遍历的结果，请重建该二叉树。假设输入的前序遍历和中序遍历的结果中都不含重复的数字。

例如，给出
前序遍历 preorder = [3,9,20,15,7]
中序遍历 inorder = [9,3,15,20,7]
返回如下的二叉树：
3
/ \\
9 20
/ \\
15 7

限制：

0 <= 节点个数 <= 5000

---

文章目录

• 1. 储备知识
• 2. 分析
• 3. 解法：递归实现
• 4. 一次优化：HashMap映射
• 5. 二次优化：传递位置参数而非复制数组
• 6.测试用例
• 7. 本题考点

---

1. 储备知识

树是一种在实际编程中经常遇到的数据结构。它的逻辑很简单:除根节点之外每个节点只有一个父节点，根节点没有父节点;除叶节点之外所有节点都有一个或多个子节点，叶节点没有子节点。父节点和子节点之间用指针链接。

由于树的操作会涉及大量的指针，因此与树有关的面试题都不太容易。当面试官想考查应聘者在有复杂指针操作的情况下写代码的能力时，他往往会想到用与树有关的面试题。

面试的时候提到的树，大部分是二叉树。所谓二叉树是树的一种特殊结构，在二叉树中每个节点最多只能有两个子节点。在二叉树中最重要的操作莫过于遍历，即按照某一顺序访问树中的所有节点。通常树有如下几种遍历方式。

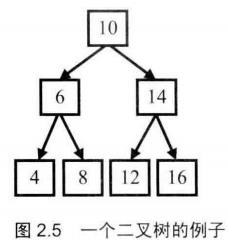
前序遍历:先访问根节点，再访问左子节点，最后访问右子节点。图中的二叉树的前序遍历的顺序是10、6、4、8、14、12、16。
中序遍历:先访问左子节点，再访问根节点，最后访问右子节点。图中的二叉树的中序遍历的顺序是4、6、8、10、12、14、16。

后序遍历:先访问左子节点，再访问右子节点，最后访问根节点。图中的二叉树的后序遍历的顺序是4、8、6、12、16、14、10。

---

---

2. 分析

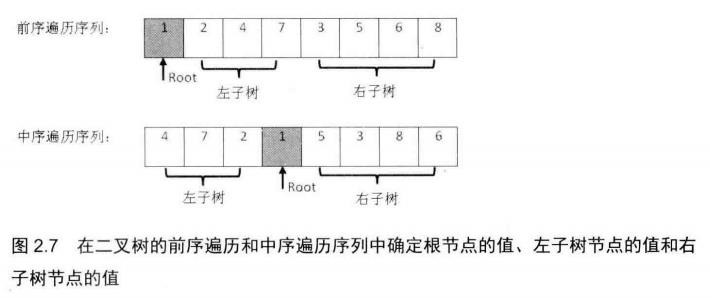
在二叉树的前序遍历序列中，第一个数字总是树的根节点的值。但在中序遍历序列中，根节点的值在序列的中间，左子树的节点的值位于根节点的值的左边，而右子树的节点的值位于根节点的值的右边。因此我们需要扫描中序遍历序列，才能找到根节点的值。

如图2.7所示，前序遍历序列的第一个数字1就是根节点的值。扫描中序遍历序列，就能确定根节点的值的位置。根据中序遍历的特点，在根节点的值1前面的3个数字都是左子树节点的值，位于1后面的数字都是右子树节点的值。

由于在中序遍历序列中，有3个数字是左子树节点的值，因此左子树共有3个左子节点。同样，在前序遍历序列中，根节点后面的3个数字就是3个左子树节点的值，再后面的所有数字都是右子树节点的值。这样我们就在前序遍历和中序遍历两个序列中分别找到了左、右子树对应的子序列。

---

---

3. 解法：递归实现

class Solution {
     public TreeNode buildTree(int[] preorder, int[] inorder) {
         int n = preorder.length;
         if(n == 0) return null;

         // 1、建立根节点
         TreeNode r = new TreeNode(preorder[0]);
         // 2、找根节点的左右节点，即在in中找pre的值
         int p = 0;
         while(inorder[p] != r.val) p++;


         // 3、分割 + 递归
         r.left = buildTree(Arrays.copyOfRange(preorder, 1, p+1), Arrays.copyOfRange(inorder, 0, p));
         r.right = buildTree(Arrays.copyOfRange(preorder, p+1, n), Arrays.copyOfRange(inorder, p+1, n));

         // 4、建树成功，返回树
         return r;
     }
 }

---

---

4. 一次优化：HashMap映射

由于解法1中每次查根节点时，都需要将数列遍历一遍，因此考虑：

定义HashMap为成员变量， 并重新构造一个方法myBuildTree()，专门提供HashMap键值对的生成，而后调用BuildTree方法，实现递归。

通过map映射每个索引所在的位置，将查找索引的级数降低至O(1)

定义两个方法的原因是：若将HashMap的映射生成定义在了方法内，每次递归都会重复进行HashMap映射的生成。

class Solution {
    // 定义为成员变量，这样类中两个方法都可以使用它
    private Map<Integer, Integer>indexMap;


    public TreeNode myBuildTree(int[] preorder, int[] inorder) {
        int n = preorder.length;
        if(n == 0) return null;
        // 1. 定义根节点
        TreeNode r = new TreeNode(preorder[0]);

        // 2、查找界限值 + 递归
        int p = indexMap.get(r.val);
        r.left = buildTree(Arrays.copyOfRange(preorder, 1, p+1), Arrays.copyOfRange(inorder, 0, p));
        r.right = buildTree(Arrays.copyOfRange(preorder, p+1, n), Arrays.copyOfRange(inorder, p+1, n));
        return r;
    }

    public TreeNode buildTree(int[] preorder, int[] inorder) {
        int n = preorder.length;
        indexMap = new HashMap<Integer, Integer>();
        for(int i = 0; i < n; i++) {
            indexMap.put(inorder[i], i);
        }

        return myBuildTree(preorder, inorder);
    }
}

---

---

5. 二次优化：传递位置参数而非复制数组

再次提交，发现耗时依然很高，仔细思考后发现，在源码中，每次递归都需要进行两次数组的复制，而每次复制的耗时为O(n)， 因此考虑：

取消数组的复制操作（copyOfRange()方法），改为使用边界值(left, right)代替，再次降低时间复杂度。

class Solution3 {
    private Map<Integer, Integer> indexMap;

    public TreeNode myBuildTree(int[] preorder, int[] inorder, int preorder_left, int preorder_right, int inorder_left, int inorder_right) {
        if (preorder_left > preorder_right) {
            return null;
        }

        // 前序遍历中的第一个节点就是根节点
        int preorder_root = preorder_left;
        // 在中序遍历中定位根节点
        int inorder_root = indexMap.get(preorder[preorder_root]);

        // 先把根节点建立出来
        TreeNode root = new TreeNode(preorder[preorder_root]);
        // 得到左子树中的节点数目
        int size_left_subtree = inorder_root - inorder_left;
        // 递归地构造左子树，并连接到根节点
        // 先序遍历中「从 左边界+1 开始的 size_left_subtree」个元素就对应了中序遍历中「从 左边界 开始到 根节点定位-1」的元素
        root.left = myBuildTree(preorder, inorder, preorder_left + 1, preorder_left + size_left_subtree, inorder_left, inorder_root - 1);
        // 递归地构造右子树，并连接到根节点
        // 先序遍历中「从 左边界+1+左子树节点数目 开始到 右边界」的元素就对应了中序遍历中「从 根节点定位+1 到 右边界」的元素
        root.right = myBuildTree(preorder, inorder, preorder_left + size_left_subtree + 1, preorder_right, inorder_root + 1, inorder_right);
        return root;
    }

    public TreeNode buildTree(int[] preorder, int[] inorder) {
        int n = preorder.length;
        // 构造哈希映射，帮助我们快速定位根节点
        indexMap = new HashMap<Integer, Integer>();
        for (int i = 0; i < n; i++) {
            indexMap.put(inorder[i], i);
        }
        return myBuildTree(preorder, inorder, 0, n - 1, 0, n - 1);
    }
}

---

---

6.测试用例

• 普通二叉树（完全二叉树、不完全二叉树）
• 特殊二叉树（退化为链表的二叉树、只有一个节点的二叉树）
• 特殊输入测试（空树、错误用例）

---

---

7. 本题考点

• 考查应聘者对二叉树前序遍历和中序遍历的理解程度
• 考查应聘者分析复杂问题的能力