音频均衡器原理及实现
Posted zuguorui
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了音频均衡器原理及实现相关的知识,希望对你有一定的参考价值。
音频均衡器原理及实现
文章目录
1. 实现原理
之前在数字信号处理系列的文章中,从卷积开始讲起,直到最后的FIR滤波器和IIR滤波器。对于滤波器最直观的应用,就是音频均衡器。
均衡器是我们经常可以见到的东西,它可以对音乐的某些频段进行增益或衰减,进而改变听感,使音频回放更具个性。尽管有很多的库可以实现这个功能,但是作为移动端开发者可能对其内在的实现机制并不了解,这篇文章将一步一步构造一个简单的均衡器。
对于均衡器,我们可以选择使用FIR滤波器或者IIR滤波器实现,两者的实现各有优劣。
使用FIR滤波器,可以最大程度保持音质,因为FIR滤波器的相位响应是线性的。可能很多人对相位的重要性不理解,考虑两个周期都为T幅度为1的正弦波信号,如果相位相差为0,那么两个完全相同的信号叠加,如果相位相差为T/2,那么就是两个反相的信号相加,得到一条y=0的直线。
但是FIR滤波器的计算量很大,主要是和音频信号的采样率以及均衡器的分辨率有关。比如你的均衡器是要处理48k采样率的音频,FIR滤波器阶数是64,那么你的频率分辨率就是48000/2/64=375Hz,这种滤波器就无法很好的调节低频,因为通常在音乐中,低频与中频的分频点一般定为125Hz左右。
IIR滤波器就在于达到相同的性能下,所需的阶数更小,但是它计算出的信号相位是非线形的,不同的频率的信号相位偏差不一致,导致最后叠加出的信号也有很大的变化,因此它对音质有一些损伤。好在在音频回放中,相位的影响基本是听不出来的。只不过需要注意相位偏移导致最后的合成信号出现溢出的情况。比如上面那个例子,两个同频同相位的信号叠加,生成的信号最大值和最小值就是两个信号的最大值和最小值之和,但是如果相位偏移,结果的信号范围就会不同。这也导致了哪怕你的IIR滤波器没有任何增益或衰减,但是仍然会影响信号可能出现溢出,因此防溢出的手段是必须的。
调节完频率之后就是防溢出,这和音频信号的形式有关系,通常音频信号以16位的有符号整数(int16或short)表示,音频信号的范围也就是int16的范围。另外一种常用的形式是32位的浮点数(float),信号范围是[-1.0, 1.0]。如果最后的信号发生了溢出,就会导致数值表达错误而造成刺耳的破音。因此,需要一定手段来使得输出信号的幅度限制在合理的范围内。
2. 方案确定
这篇文章将构造一个三分频的均衡器,可以独立调节低频中频和高频。
在动手之前,我们先分析一下需求。三分频均衡器,并不是将整个频率平均分成三等分,对于音乐来说,大部分信息都集中在中低频,通常将200Hz以下看作低频,这部分要求最好只影响鼓和贝斯,最好不要影响人声,这样能够使调节效果显得非常纯净;200~4kHz则是大部分乐器和人声所在的区域,这是中频;在4kHz以上的则是高频。中高频的分频点并不好确定,我这是按照个人理解,希望能在调节中高频EQ时能够有比较明显的效果,大部分乐器和人声的音域是能够跨过4kHz的,这样可以调节音乐中主要信号的明暗,如果分频点定得过高,那么能影响的信号就非常少,导致体验不够明显。
假定我们的系统是要处理48kHz的信号,如果使用FIR滤波器,由于低频范围最窄,是200Hz,那么就要求我们的滤波器分辨率最少要达到200Hz,那么计算一下所需的阶数是48000/2/200 = 120。
如果使用IIR滤波器,由于我们构造的滤波器是4种基本滤波器(低通、带通、高通、带阻),在复杂的需求下,我们需要组合滤波器:串联或并联。但是IIR滤波器的相位响应是非线形的,串联滤波器的相位响应是组成它的滤波器的相位响应之和,所以为了避免音频信号的相位响应过于劣化,我们选择并联IIR滤波器。
3. 使用FIR滤波器
使用FIR滤波器构造均衡器并不是本篇文章的重点,因为它的原理实在太简单了,参考前面博客《数字信号处理5:FIR滤波器设计》就足够了,因为FIR滤波器天生可以针对不同的频率设置不同的增益值,因此一个滤波器就足以完成均衡器的任务。
这里大体说一下构造步骤:
- 根据均衡器设置生成FIR滤波器的频域的幅度响应。根据实际表现,可能需要对幅度响应做一些平滑,避免相邻频率增益差别过大导致波纹。
- 构造相位响应,与幅度响应结合,成为FIR滤波器的频域响应,这一步相对比较固定。
- 对FIR滤波器的频域响应使用傅立叶逆变换,然后加窗,得到时域滤波器。之后使用该滤波器与信号进行卷积即可。
缺点:
- 每次重新调整增益,都要重新生成一次滤波器,可能会导致用户交互上的问题。当然,你也可以选择像IIR滤波器并联一样(下节会讲),使用多个基本FIR滤波器并联,只调节幅度,但是这样的计算成本太高了。
- 阶数太高,计算代价大。
优点:
- 音质损伤较小。
- 有限字长效应带来的影响较小,稳定性好,编程调试难度低。
- 对于多阶均衡器比较适用,许多比较专业的均衡器可以控制相当多频段的增益,这种情况下相比于并联IIR滤波器,直接使用一个FIR滤波器反而要方便得多。
- FIR滤波器生成的过程比较简单,容易编写为代码,因此可以随时从0构造一个FIR滤波器。当你修改了一些核心参数导致影响到了FIR滤波器结构,比如采样率和频率分辨率之类的,可以重新生成一个结构不同的滤波器。但IIR滤波器是从模拟滤波器开始的,这一点比FIR滤波器更为复杂。
4. 使用IIR滤波器
之前提到,我们生成的IIR滤波器都是四种基本类型滤波器,如果有更复杂的滤波要求,就需要将它们并联起来。对于三分频均衡器,我们使用一个低通、带通和高通滤波器并联,将原始信号分别给三个滤波器进行处理,然后将处理结果相加进行合并,就得到了最终结果。增益控制则是很简单地使用一个系数去乘对应滤波器的输出即可。这样一来,我们可以对用户的增益设置做出非常迅速且平滑的响应,而不必像FIR滤波器一样每次调节增益都需要重新生成滤波器。
对于三个滤波器类型的选取,我选择了切比雪夫II型滤波器,因为它所需的阶数比巴特沃兹少,并且通带是平坦的。我们让三个滤波器在阻带的衰减都为40dB。
三个滤波器的频率指标如下:
- 低通:0~200Hz
- 带通:200~4kHz
- 高通:4k~Fs/2Hz
Fs为采样率。
注意,以上只是一个理想的频率分割,在实际设计滤波器的时候,低通和带通、带通和高通之间会出现交汇,我们可能需要经过几次实验来让交汇的部分在最后相加的时候既不会塌陷也不会冒出,保证在0增益的时候频率分布和原曲尽量接近。
接下来使用matlab生成我们需要的滤波器。代码如下:
clear all
close all
sampleRate = 48000;
maxFreq = sampleRate / 2;
[lp_N, lp_Wn] = cheb2ord(180 / maxFreq, 360 / maxFreq, 1, 40);
[lp_b, lp_a] = cheby2(lp_N, 40, lp_Wn, 'low');
figure
freqz(lp_b, lp_a);
title("lowpass");
[lp_sos, lp_g] = tf2sos(lp_b, lp_a);
[bp_N, bp_Wn] = cheb2ord([400, 3000] / maxFreq, [150, 6000] / maxFreq, 1, 40);
[bp_b, bp_a] = cheby2(bp_N, 40, bp_Wn, 'bandpass');
figure
freqz(bp_b, bp_a);
title("bandpass")
[bp_sos, bp_g] = tf2sos(bp_b, bp_a);
[hp_N, hp_Wn] = cheb2ord(5000 / maxFreq, 2500 / maxFreq, 1, 40);
[hp_b, hp_a] = cheby2(hp_N, 40, hp_Wn, 'high');
figure
freqz(hp_b, hp_a);
title("highpass")
[hp_sos, hp_g] = tf2sos(hp_b, hp_a);
可以看到我并不是严格按照频率指标去做的,而是争取在让各个滤波器滚降的一半交汇,这样避免了频率失真。得到的响应如下:
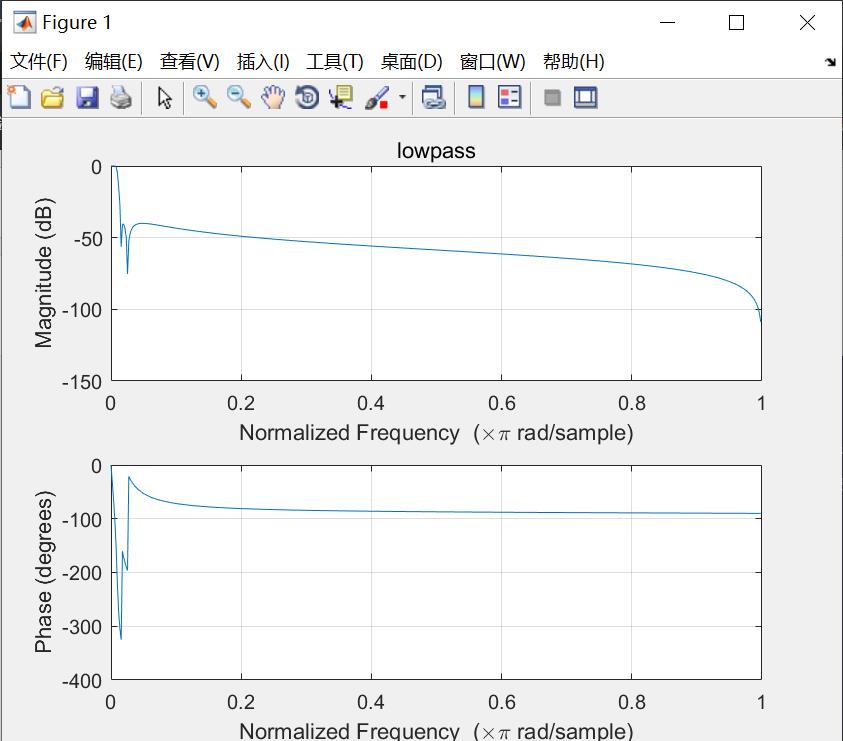
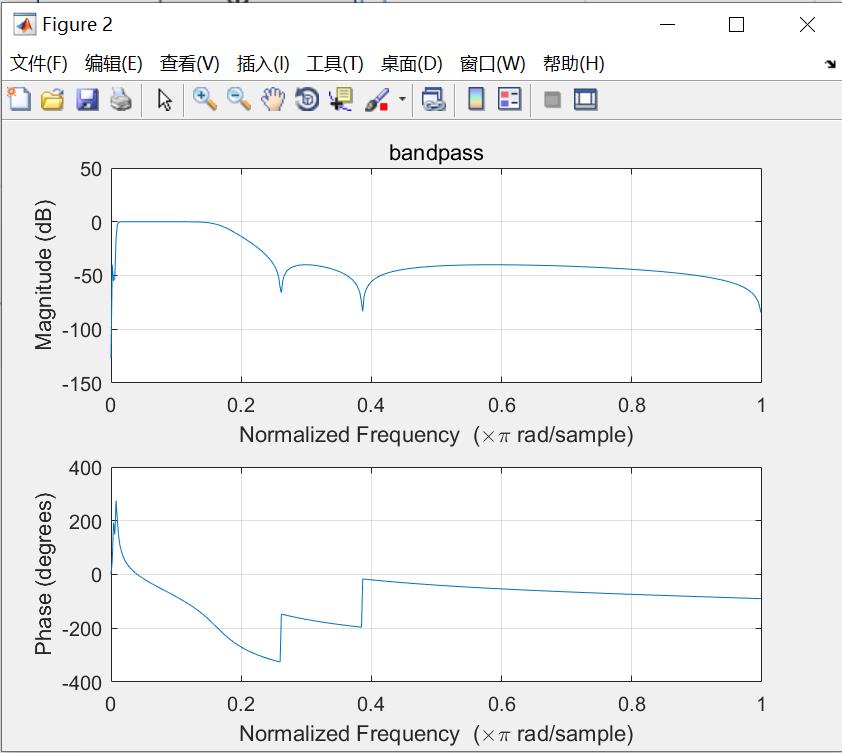
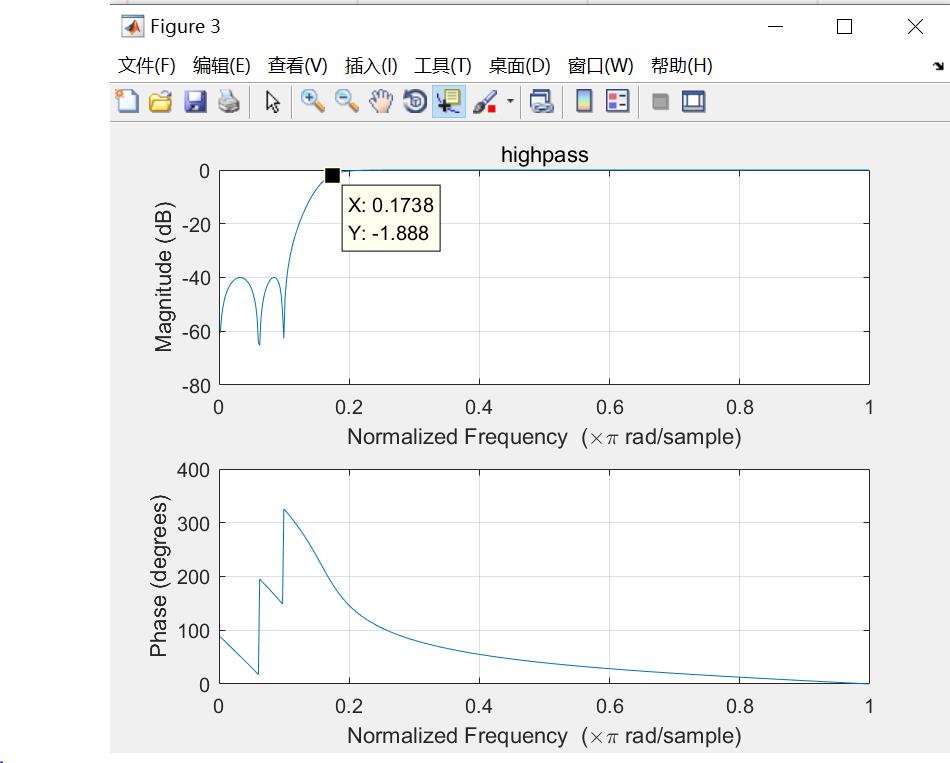
因为低频的分频点过于低,所以不是很容易看清楚。
优点:
- 计算快捷。
- 增益调节平滑。
缺点:
- 有限字长效应带来的影响非常严重,必须小心设计和调试。
- 一些关键参数改变时,比如采样率,无法方便地从零开始重新构造滤波器。你也可以将构造滤波器的部分编写成代码,但是这部分非常复杂,灵活性较差。
- 非线性相位响应,影响音质。
- 无法很好地适合多段均衡器。
接下来是设计程序。使用c++代码。
4.1 IIR滤波器程序实现
#ifndef _IIR_FILTER_H_
#define _IIR_FILTER_H_
#include <iostream>
#include <stdlib.h>
#include <stdint.h>
#include <list>
#include <memory>
using namespace std;
/**
* IIR滤波器
*
*/
class IIRFilter{
public:
// 滤波器类型,TYPE_NORMAL代表基本形态的滤波器,TYPE_SOS代表级联形式的滤波器,它内部包含多个基本滤波器
static const int TYPE_NORMAL = 0;
static const int TYPE_SOS = 1;
/**
* 基本形态滤波器的构造函数
* @param b: 滤波器中x的系数
* @param a: 滤波器中y的系数
* @param len: a和b的长度
* @param maxSamplesPerBuffer: 每次处理的最长buffer大小,用来创建缓存用,避免频繁申请和释放内存
*/
IIRFilter(double *b, double *a, int len, int maxSamplesPerBuffer);
/**
* sos级联形式滤波器的构造函数
* @param sos: sos矩阵
* @param g: 滤波器总增益系数
* @param sosRows: sos矩阵行数,相当于级联滤波器的个数
* @param sosCols: sos矩阵列数
* @param maxSamplesPerBuffer: 每次处理的最长buffer大小,用来创建缓存用,避免频繁申请和释放内存
*
*/
IIRFilter(double **sos, double g, int sosRows, int sosCols, int maxSamplesPerBuffer);
~IIRFilter();
/**
* 获取滤波器类型,是基本型还是级联型
*/
int getType();
/**
* 处理数据,双声道
* @param input: 输入buffer
* @param output: 输出buffer
* @param samples: buffer有多少帧,对于双声道数据,一帧包含左右声道两个double
*
*/
void process(double *input, double *output, int samples);
private:
// 更新滤波器中的x缓存
void updateX(double x);
// 更新滤波器的y缓存
void updateY(double y);
void processNormal(double *input, double *output, int len);
void processSOS(double *input, double *output, int len);
// 滤波器中的系数组a
double *filter_a = nullptr;
// 滤波器中的系数组b
double *filter_b = nullptr;
// 滤波器中的系数个数
int coefficientCount;
// x和y缓存,因为经常要将新值push进去,所以采用list实现
list<double> xs;
list<double> ys;
int maxSamplesPerBuffer;
// 级联形式的缓存
double *sosInput = nullptr;
double *sosOutput = nullptr;
// 级联形式下,级联滤波器里包含多个低阶滤波器
list<shared_ptr<IIRFilter>> subFilters;
// 级联滤波器的总增益系数
double g = 1;
int filterType = TYPE_NORMAL;
};
#endif
#include "IIRFilter.h"
#include <assert.h>
#include <chrono>
IIRFilter::IIRFilter(double *b, double *a, int len, int maxSamplesPerBuffer)
{
filterType = TYPE_NORMAL;
this->coefficientCount = len;
this->maxSamplesPerBuffer = maxSamplesPerBuffer;
filter_b = (double *)malloc(coefficientCount * sizeof(double));
memcpy(filter_b, b, coefficientCount * sizeof(double));
filter_a = (double *)malloc((coefficientCount - 1) * sizeof(double));
memcpy(filter_a, a + 1, (coefficientCount - 1) * sizeof(double));
// 初始化x和y缓存
for(int i = 0; i < coefficientCount; i++)
{
xs.push_back(0);
}
for(int i = 0; i < coefficientCount - 1; i++)
{
ys.push_back(0);
}
}
IIRFilter::IIRFilter(double **sos, double g, int sosRows, int sosCols, int maxSamplesPerBuffer)
{
filterType = TYPE_SOS;
this->g = g;
this->maxSamplesPerBuffer = maxSamplesPerBuffer;
sosInput = (double *)malloc(maxSamplesPerBuffer * sizeof(double));
sosOutput = (double *)malloc(maxSamplesPerBuffer * sizeof(double));
int coefficientCount = sosCols / 2;
for(int i = 0; i < sosRows; i++)
{
double *ba = sos[i];
double *b = (double *)malloc(coefficientCount * sizeof(double));
memcpy(b, ba, coefficientCount * sizeof(double));
double *a = (double *)malloc(coefficientCount * sizeof(double));
memcpy(a, ba + coefficientCount, coefficientCount * sizeof(double));
shared_ptr<IIRFilter> filter(new IIRFilter(b, a, coefficientCount, maxSamplesPerBuffer));
subFilters.push_back(filter);
}
}
IIRFilter::~IIRFilter()
{
if(sosInput != nullptr)
{
free(sosInput);
}
if(sosOutput != nullptr)
{
free(sosOutput);
}
}
void IIRFilter::updateX(double x){
xs.push_front(x);
xs.pop_back();
}
void IIRFilter::updateY(double y)
{
ys.push_front(y);
ys.pop_back();
}
void IIRFilter::process(double *input, double *output, int samples)
{
if(filterType == TYPE_NORMAL)
{
processNormal(input, output, samples);
}
else{
processSOS(input, output, samples);
}
}
void IIRFilter::processNormal(double *input, double *output, int samples)
{
chrono::system_clock::time_point start = chrono::system_clock::now();
for(int i = 0; i < samples; i++)
{
// 首先,将新的x值更新到x缓存中
updateX(input[i]);
double feedforwardSum = 0;
int filterIndex = 0;
// 计算前向反馈和
for(double x : xs)
{
double f = filter_b[filterIndex];
feedforwardSum += (f * x);
filterIndex++;
}
filterIndex = 0;
double feedbackSum = 0;
// 计算后向反馈和
for(double y : ys)
{
double f = filter_a[filterIndex];
feedbackSum += (f * y);
filterIndex++;
}
double d = feedforwardSum - feedbackSum;
output[i] = d;
// 将结果更新到y缓存中
updateY(d);
}
chrono::system_clock::time_point end = chrono::system_clock::now();
chrono::microseconds duration = chrono::duration_cast<chrono::microseconds>(end - start);
//cout << "normal process " << samples << "samples use " << duration.count() << "us" << endl;
}
void IIRFilter::processSOS(double *input, double *output, int samples)
{
assert(samples <= maxSamplesPerBuffer);
chrono::system_clock::time_point start = chrono::system_clock::now();
memcpy(sosInput, input, samples * sizeof(double));
for(shared_ptr<IIRFilter> filter : subFilters)
{
filter->process(sosInput, sosOutput, samples);
double *temp = sosInput;
sosInput = sosOutput;
sosOutput = temp;
}
// 注意这里,最后一个子滤波器处理完毕后,处理结果会被sosInput指向而不是sosOutput
for(int i = 0; i < samples; i++)
{
output[i] = sosInput[i] * g;
}
chrono::system_clock::time_point end = chrono::system_clock::now();
chrono::microseconds duration = chrono::duration_cast<chrono::microseconds>(end - start);
cout << "SOS process " << samples << "samples use " << duration.count() << "us" << endl;
}
4.2 EQ均衡器实现
#ifndef _EQUALIZER_H_
#define _EQUALIZER_H_
#include <iostream>
#include <stdlib.h>
#include <memory>
#include <stdint.h>
#include <cmath>
#include <vector>
#include "IIRFilter.h"
#include "DynamicCompressor.h"
using namespace std;
/**
* 声道道均衡器,我们为每个声道都要建立一个均衡器
*
*/
class ChannelFilter
{
public:
shared_ptr<IIRFilter> lowPassFilter;
shared_ptr<IIRFilter> bandPassFilter;
shared_ptr<IIRFilter> highPassFilter;
~ChannelFilter()
{
lowPassFilter.reset();
bandPassFilter.reset();
highPassFilter.reset();
}
};
// 正常形式的低通滤波器系数
static const int LP_LEN = 6;
static double LP_B[LP_LEN] = {0.00112266916511878, -0.00335804481007404, 0.00223539333478608, 0.00223539333478608, -0.00335804481007404, 0.00112266916511878};
static double LP_A[LP_LEN] = {1, -4.89871336422332, 9.59996411771510, -9.40745163011783, 4.60986753597724, -0.903666623971535};
// 正常形式的带通滤波器系数
static const int BP_LEN = 11;
static double BP_B[BP_LEN] = {0.0147870348410641, -0.0896713907921595, 0.239728170511116, -0.357933513532618, 0.281432905082980, -1.31335252371870e-17, -0.281432905082980, 0.357933513532618, -0.239728170511116, 0.0896713907921597, -0.0147870348410641};
static double BP_A[BP_LEN] = {1, -8.24143236474598, 30.6837048158386, -67.9994348029134, 99.3786343355872, -100.107651076046, 70.4028934601109, -34.1345683881885, 10.9193043553503, -2.08073159058107, 0.179281256060903};
// 正常形式的高通滤波器系数
static const int HP_LEN = 6;
static double HP_B[HP_LEN] = {0.512554073443323, -2.49431022188030, 4.92200130950305, -4.92200130950306, 2.49431022188030, -0.512554073443323};
static double HP_A[HP_LEN] = {1, -3.56799305163320, 5.31535809874652, -4.09208228010496, 1.61958624530545, -0.262711533863224};
// 级联形式的低通滤波器参数
static const int LP_SOS_ROW = 3;
static const int LP_SOS_COL = 6;
static const double LP_SOS[LP_SOS_ROW][LP_SOS_COL] = {
{1, 1.00000000000000, 0, 1, -0.963547075321816, 0},
{1, -1.99358039818411, 0.999999999999900, 1, -1.95062963869978, 0.951737145504358},
{1, -1.99754549571959以上是关于音频均衡器原理及实现的主要内容,如果未能解决你的问题,请参考以下文章