二叉搜索树
Posted ych9527
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了二叉搜索树相关的知识,希望对你有一定的参考价值。
1.二叉搜索树是什么
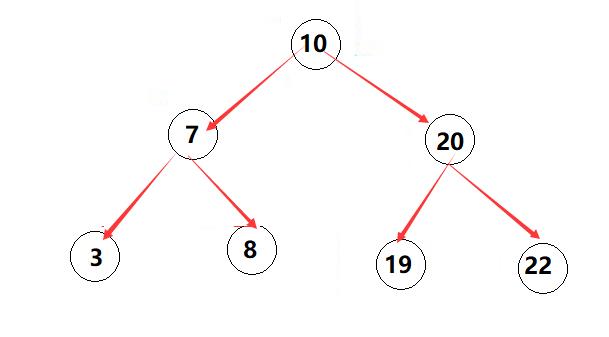
二叉搜索树又称二叉排序树,它或者是一棵空树,或者是具有以下性质的二叉树:
若它的左子树不为空,则左子树上所有节点的值都小于根节点的值
若它的右子树不为空,则右子树上所有节点的值都大于根节点的值
它的左右子树也分别为二叉搜索树
2.二叉搜索树的实现
2.1二叉搜索树的插入
1.如果为空,则直接插入
2.如果不为空,则需要按照二叉搜索树的性质寻找插入的位置,插入新节点:
给定parent,cur两个指针,parent记录cur的父节点
key大于当前节点,则cur往右边走,key小于当前节点则cur往左边走,如果等于返回false(不允许相等)
当节点为空的时候,再拿key和parent节点的值进行比较,如果小于parent对应的值,则连接在左边,否则连接在右边
2.2 二叉搜索树的查找
根节点不为空时:
如果当前值大于查找值,往左走
如果当前值小于查找值,往右走
如果等于返回true
根节点为空时:
返回false
查找时间复杂度:
当二叉树退化成链表时:O(N),如果是平衡二叉搜索树,时间复杂度接近log(N)
2.3二叉搜索树的删除
首先查找元素是否在树之中,如果不存在返回。
存在的话要删除的节点可能有下面四种情况:
1.要删除的节点没有孩子节点 -> 直接删除
2.要删除的节点只有左孩子节点 -> 父节点连接它的左节点、删除节点
3.要删除的孩子只有右孩子节点 -> 父节点连接它的右节点、删除节点
4.要删除的孩子有左右孩子节点 -> 找到以该节点为根节点的,左子树的最大值或者右子树的最小值,替换根节点,然后删除该节点
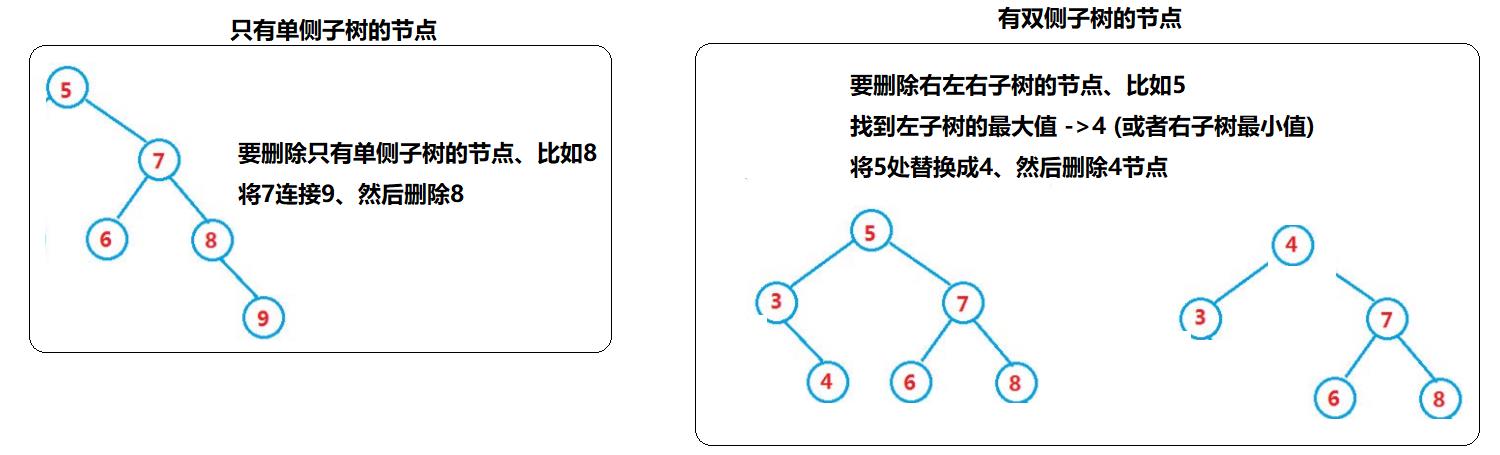
注意:
1.删除叶子节点的时候,可以将叶子节点和删除单侧节点进行合并
2.删除的节点只有一侧子树时,需要注意当前节点是不是根节点


3.二叉搜索树的应用
1.K模型:
只有key值作为关键码,应用时查找key值即可。比如排序去重,门禁卡(查找在不在),检查单词是否正确(set)
2.KV模型:
每一个关键码都有对应的value值,即<key,value>的键值对。(map)
KV模型在K模型应用的基础上,增加了一些用法。
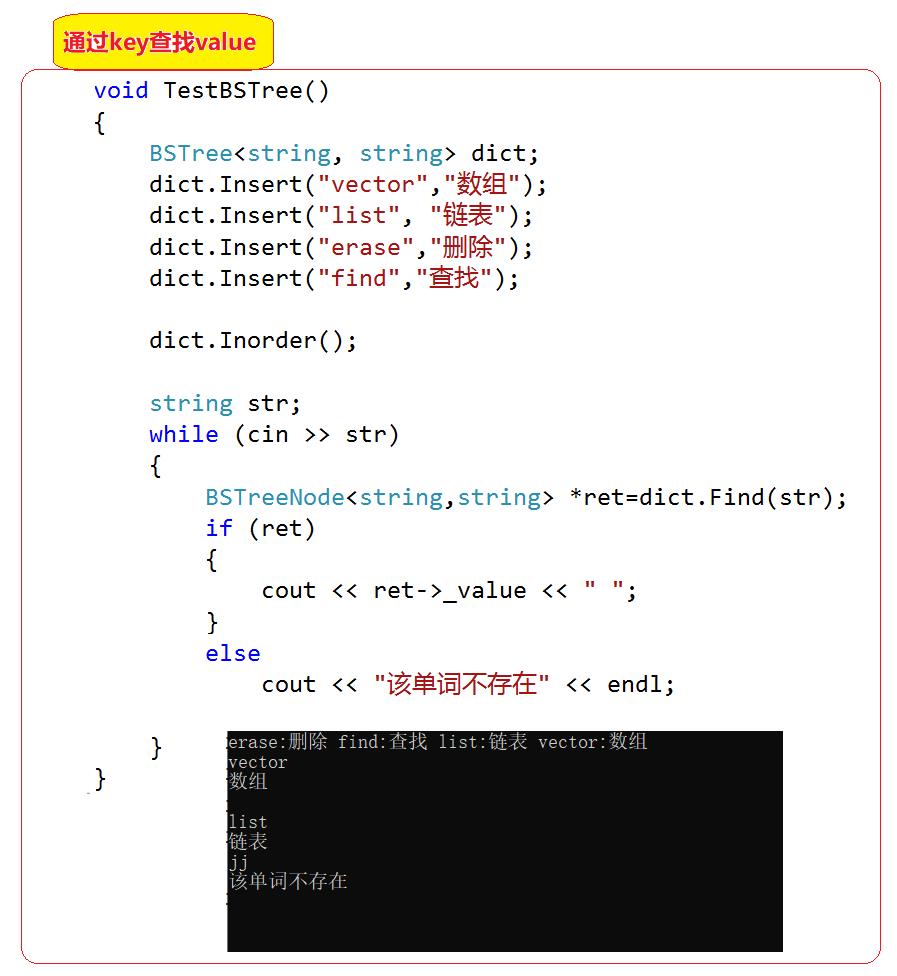
比如:中英对应字典,通过中文查找英文,统计次数
4.实现代码
4.1 K的搜索模型
#include <iostream>
using namespace std;
#include <windows.h>
template<class K>
struct BSTreeNode
{
BSTreeNode(const K&key)
:_key(key)
, left(nullptr)
, right(nullptr)
{}
K _key;
BSTreeNode *left;
BSTreeNode *right;
};
template<class K>
class BSTree
{
typedef BSTreeNode<K> Node;
public:
bool Insert(const K &key)
{
if (_root == nullptr)
{
_root = new Node(key);//构造一个根节点
return true;
}
Node *parent = nullptr;
Node *cur = _root;
while (cur)
{
if (cur->_key > key)
{
parent = cur;
cur = cur->left;
}
else if (cur->_key < key)
{
parent = cur;
cur = cur->right;
}
else
{
return false;//不允许相等
}
}
Node *newnode = new Node(key);
if (parent->_key > key)
parent->left = newnode;
else
parent->right = newnode;
return true;
}
void _Inorder(Node *root)
{
if (!root)
return;
_Inorder(root->left);
cout << root->_key << " ";
_Inorder(root->right);
}
//遍历需要传入根节点
//在外面无法拿到root(private)
//因此需要封装一层
void Inorder()
{
_Inorder(_root);
cout << endl;
}
const Node *Find(const K&key)//K值模式、不允许改
{
Node *cur = _root;
while (cur)
{
if (cur->_key > key)
cur = cur->left;
else if (cur->_key < key)
cur = cur->right;
else
return cur;
}
return nullptr;
}
bool Erase(const K&key)
{
Node *parent = nullptr;
Node *cur = _root;
while (cur)
{
if (cur->_key > key)
{
parent = cur;
cur = cur->left;
}
else if (cur->_key < key)
{
parent = cur;
cur = cur->right;
}
else//找到了、准备进行删除
{
if (cur->left == nullptr)//左子树为空
{
if (cur == _root)//特殊情况:删除根
{
_root = cur->right;
}
else
{
if (parent->left == cur)//为父节点的左子树
{
parent->left = cur->right;
}
else if (parent->right == cur)//为父节点的右子树
{
parent->right = cur->right;
}
}
delete cur;
}
else if (cur->right == nullptr)//右子树为空
{
if (cur == _root)//特殊情况:删除根
_root = cur->left;
else
{
if (parent->left == cur)//为父节点的左子树
{
parent->left = cur->left;
}
else if (parent->right == cur)//为父节点的右子树
{
parent->right = cur->left;
}
}
delete cur;
}
else//左右子树都不为空、替代法删除
{
Node *smParent = cur;//不能给空、防止Submax就是根
Node *SubMax = cur->left;//找左树的最大值
while (SubMax->right)//不断的往右走
{
smParent = SubMax;
SubMax = SubMax->right;
}
//找到了左树的最大节点、挪到cur处&&submax一定是右为空的节点
cur->_key = SubMax->_key;//替代
if (smParent->right == SubMax)//父节点右边连接
smParent->right = SubMax->left;
else//父节点左边连接
smParent->left = SubMax->left;
delete SubMax;//释放替代节点
}
return true;
}
}
return false;//表示没有找到
}
private:
Node *_root=nullptr;
};
#include "BSTree.hpp"
void TestBSTree()
{
BSTree<int> tree;
tree.Insert(5);
tree.Insert(3);
tree.Insert(7);
tree.Insert(1);
tree.Insert(4);
tree.Insert(6);
tree.Insert(8);
tree.Insert(0);
tree.Insert(2);
tree.Insert(9);
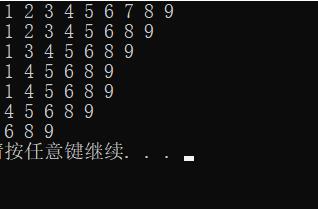
tree.Inorder();
tree.Erase(7);
tree.Inorder();
tree.Erase(2);
tree.Inorder();
tree.Erase(3);
tree.Inorder();
tree.Erase(2);
tree.Inorder();
tree.Erase(1);
tree.Inorder();
tree.Erase(0);
tree.Erase(3);
tree.Erase(4);
tree.Inorder();
}
int main()
{
TestBSTree();
system("pause");
return 0;
}
4.2 KV模型
#include <iostream>
using namespace std;
#include <windows.h>
#include <string>
template<class K,class V>
struct BSTreeNode
{
BSTreeNode(const K&key,const V&value)
:_key(key)
, _value(value)
, left(nullptr)
, right(nullptr)
{}
const K _key;//KV模式、key不允许修改
V _value;
BSTreeNode *left;
BSTreeNode *right;
};
template<class K,class V>
class BSTree
{
typedef BSTreeNode<K,V> Node;
public:
bool Insert(const K &key,const V &value)
{
if (_root == nullptr)
{
_root = new Node(key,value);//构造一个根节点
return true;
}
Node *parent = nullptr;
Node *cur = _root;
while (cur)
{
if (cur->_key > key)
{
parent = cur;
cur = cur->left;
}
else if (cur->_key < key)
{
parent = cur;
cur = cur->right;
}
else
{
return false;//不允许相等
}
}
Node *newnode = new Node(key,value);
if (parent->_key > key)
parent->left = newnode;
else
parent->right = newnode;
return true;
}
void _Inorder(Node *root)
{
if (!root)
return;
_Inorder(root->left);
cout << root->_key << ":" << root->_value << " ";
_Inorder(root->right);
}
//遍历需要传入根节点
//在外面无法拿到root(private)
//因此需要封装一层
void Inorder()
{
_Inorder(_root);
cout << endl;
}
Node *Find(const K&key)//KV模式、value允许修改
{
Node *cur = _root;
while (cur)
{
if (cur->_key > key)
cur = cur->left;
else if (cur->_key < key)
cur = cur->right;
else
return cur;
}
return nullptr;
}
bool Erase(const K&key)
{
Node *parent = nullptr;
Node *cur = _root;
while (cur)
{
if (cur->_key > key)
{
parent = cur;
cur = cur->left;
}
else if (cur->_key < key)
{
parent = cur;
cur = cur->right;
}
else//找到了、准备进行删除
{
if (cur->left == nullptr)//左子树为空
{
if (cur == _root)//特殊情况:删除根
{
_root = cur->right;
}
else
{
if (parent->left == cur)//为父节点的左子树
{
parent->left = cur->right;
}
else if (parent->right == cur)//为父节点的右子树
{
parent->right = cur->right;
}
}
delete cur;
}
else if (cur->right == nullptr)//右子树为空
{
if (cur == _root)//特殊情况:删除根
_root = cur->left;
else
{
if (parent->left == cur)//为父节点的左子树
{
parent->left = cur->left;
}
else if (parent->right == cur)//为父节点的右子树
{
parent->right = cur->left;
}
}
delete cur;
}
else//左右子树都不为空、替代法删除
{
Node *smParent = cur;//不能给空、防止Submax就是根
Node *SubMax = cur->left;//找左树的最大值
while (SubMax->right)//不断的往右走
{
smParent = SubMax;
SubMax = SubMax->right;
}
//找到了左树的最大节点、挪到cur处&&submax一定是右为空的节点
cur->_key = SubMax->_key;//替代
if (smParent->right == SubMax)//父节点右边连接
smParent->right = SubMax->left;
else//父节点左边连接
smParent->left = SubMax->left;
delete SubMax;//释放替代节点
}
return true;
}
}
return false;//表示没有找到
}
private:
Node *_root=nullptr;
};
#include "BSTree.hpp"
void TestBSTree()
{
//BSTree<string, string> dict;
//dict.Insert("vector","数组");
//dict.Insert("list", "链表");
//dict.Insert("erase","删除");
//dict.Insert("find","查找");
//dict.Inorder();
//string str;
//while (cin >> str)
//{
// BSTreeNode<string,string> *ret=dict.Find(str);
// if (ret)
// {
// cout << ret->_value << " ";
// }
// else
// cout << "该单词不存在" << endl;
//}
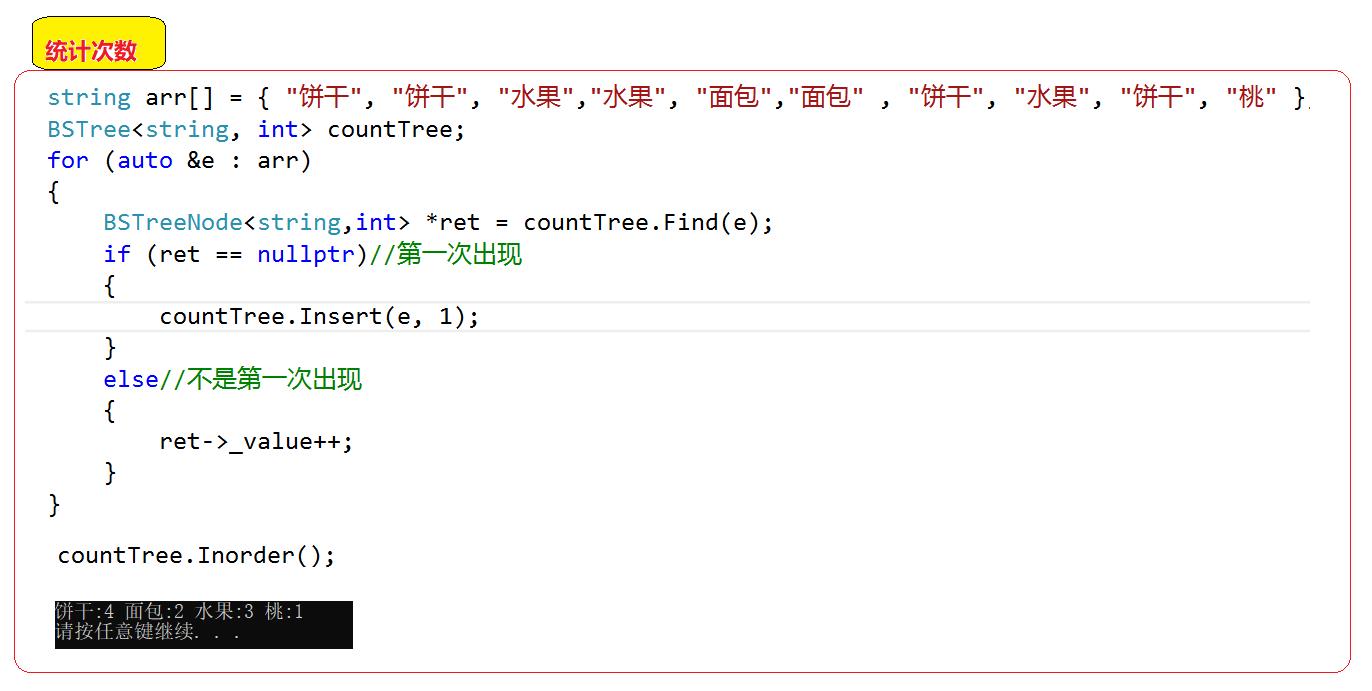
string arr[] = { "饼干", "饼干", "水果","水果", "面包","面包" , "饼干", "水果", "饼干", "桃" };
BSTree<string, int> countTree;
for (auto &e : arr)
{
BSTreeNode<string,int> *ret = countTree.Find(e);
if (ret == nullptr)//第一次出现
{
countTree.Insert(e, 1);
}
else//不是第一次出现
{
ret->_value++;
}
}
countTree.Inorder();
}
int main()
{
TestBSTree();
system("pause");
return 0;
}
以上是关于二叉搜索树的主要内容,如果未能解决你的问题,请参考以下文章