红黑树的实现mapset的封装
Posted ych9527
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了红黑树的实现mapset的封装相关的知识,希望对你有一定的参考价值。
1.红黑树概念、性质
1.1什么是红黑树
红黑树,是一种二叉搜索树,但是在每个节点上增加了一个存储位,标识节点的颜色,可以是RED或者BLACK。通过对任何一条从根到叶子的路径上各个节点着色方式的限制,红黑树确保没有一条路径会比其它的路径长出两倍(最长路径<=2倍最短路径),因此是接近平衡的
1.2红黑树的性质
1.每个节点不是红色就是黑色的
2.根节点是黑色的
3.没有连续的两个红色节点
4.对于每个节点,从该节点到其后代叶节点的路径上,均包含相同的黑色节点(每条路径上的黑色节点的总数是相同的)
5.每个叶子节点都是黑色的(这里的叶子节点指的是空节点)
1.3性质分析
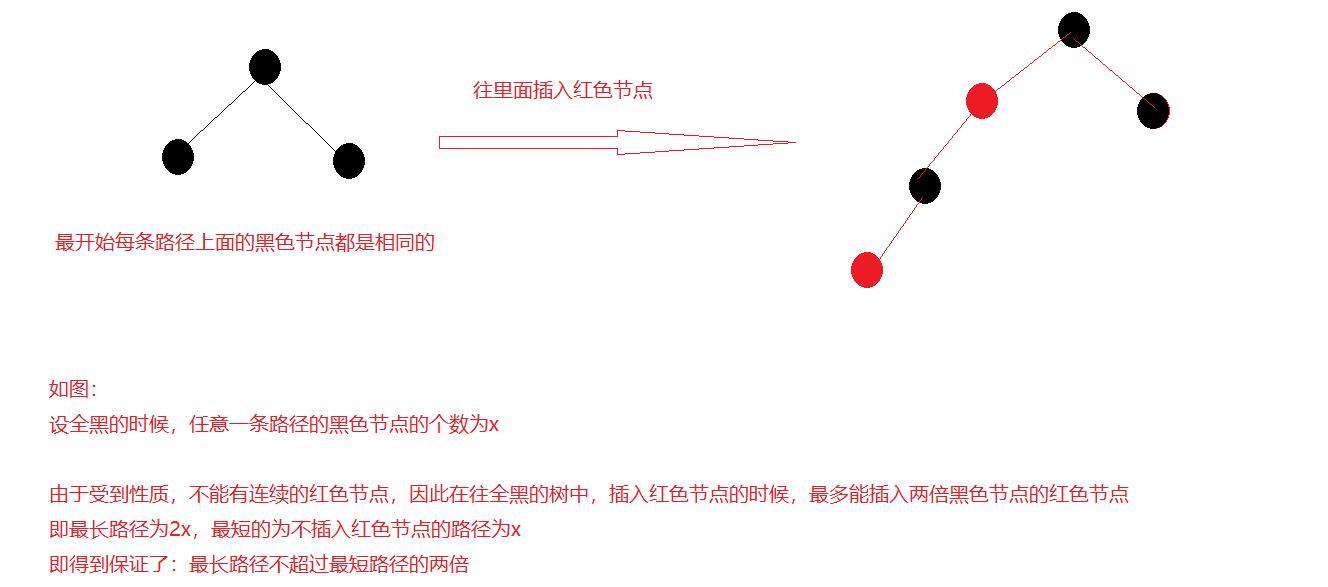
1.3.1为什么满足1.2的性质,就能保证最长路径不会超过最短路径的两倍
1.3.2与AVL树进行效率比较
设红黑树的黑色节点数为x个,任意一颗红黑树中,总结点的个数N为[x,2x],即查找的效率为 logN~log2N -> logN~log2N 即O(logN)
但是在底层实现之中,AVL是严格的平衡二叉树,红黑树只是近似平衡二叉树,即AVL树要进行更多的旋转操作,因此红黑树的性能更优于AVL树。我们常用的set和map在底层用的就是红黑树
2.红黑树底层构建情况分析
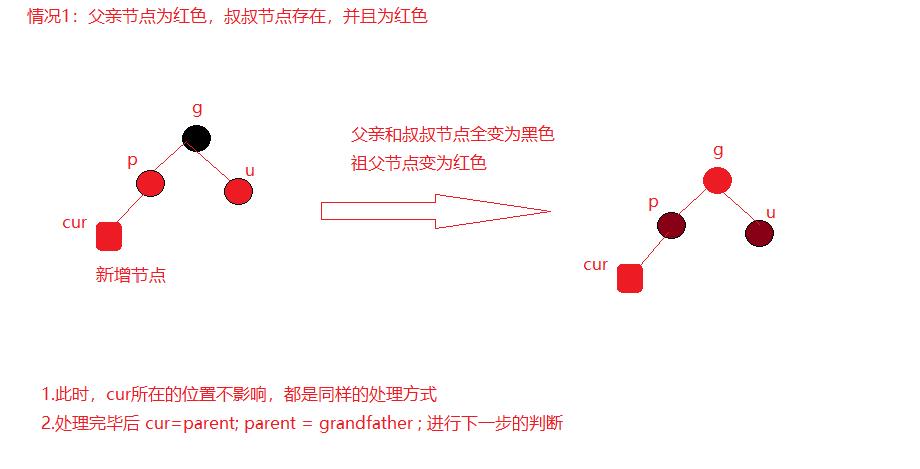
2.1父亲节点为红色,叔叔节点存在,并且为红色
2.2父亲节点为红色,叔叔节点不存在或者存在且为黑色
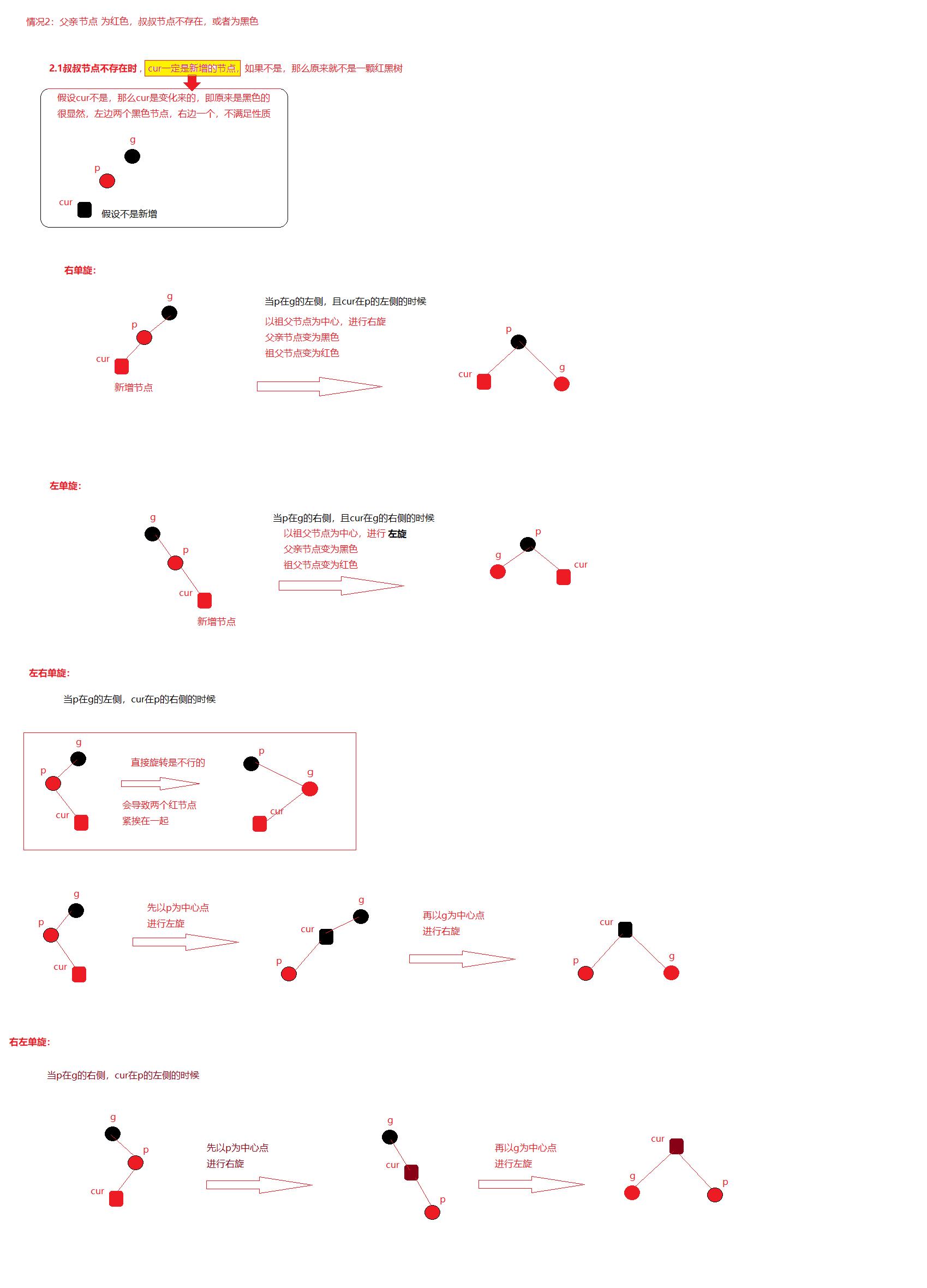
2.2.1叔叔节点不存在
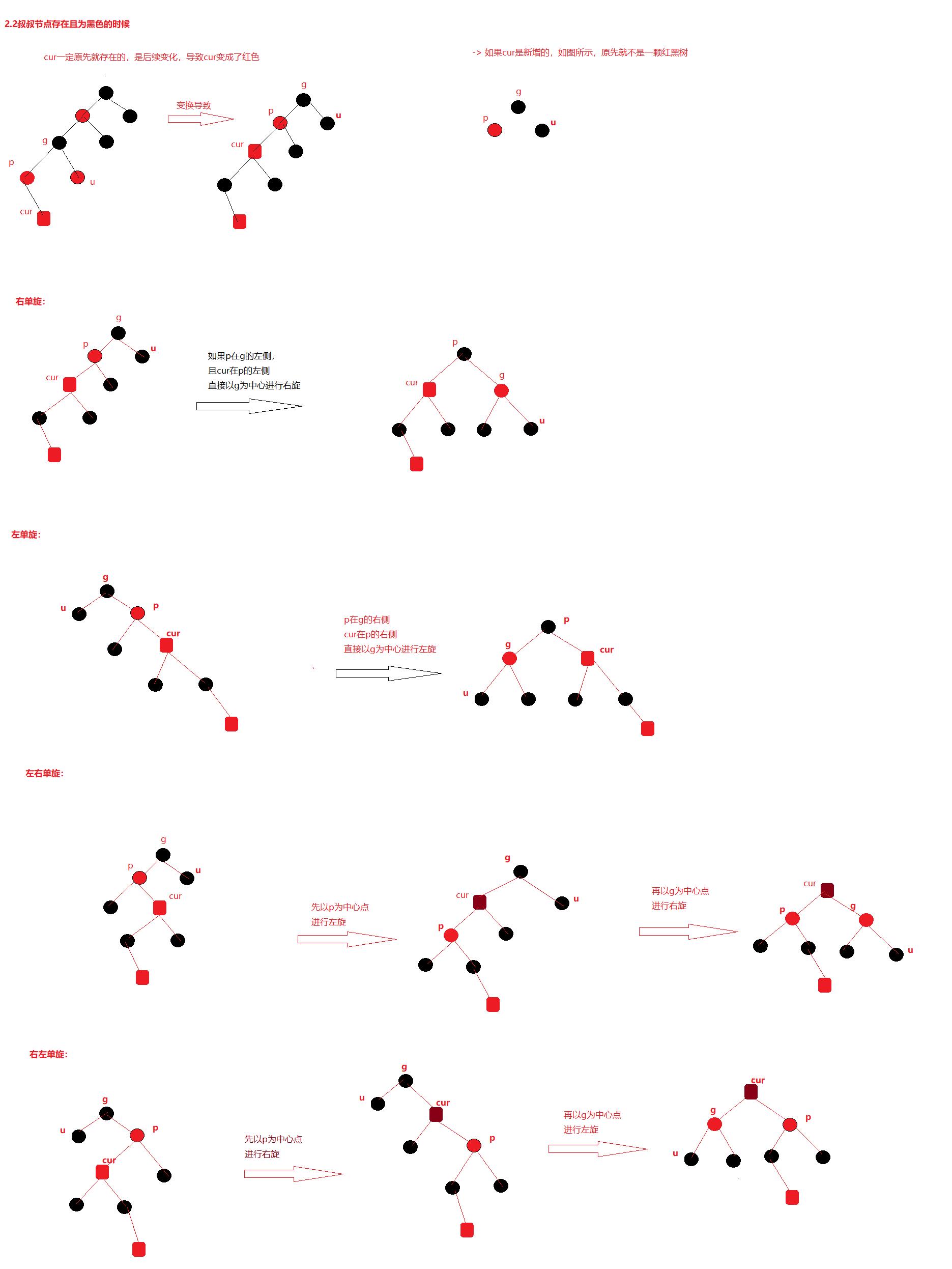
2.2.2叔叔节点存在,且为黑色
2.3总结
由上述分析可知,红黑树的构建主要分为如下情况
1.父亲节点为黑色,插入的节点为红色,不需要进行操作
2.父亲节点和叔叔节点为红色,插入一个红色的节点后,父亲节点和叔叔节点变为黑色,祖父节点变为红色
3.父亲节点为红色、叔叔节点不存在或者为黑色:
当parent在grandfather左侧时:
cur在parent左侧 -> 以g为中心,进行右旋,并且g变为红色,p变为黑色(右旋)
cur在parent右侧 -> 先以p为中心进行左旋,再以g为中心进行右旋(左右双旋)
当parent在grandfather右侧时:
cur在parent右侧 -> 以g为中心,进行左旋,并且g变为红色,p变为黑色(左旋)
cur在parent左侧 -> 先以p为中心进行右旋,再以g为中心进行左旋(右左双旋)
3.实现代码和验证
3.1实现代码
#pragma once
#include <iostream>
using namespace std;
enum Color
{
RED,
BLACK
};
template<class K,class V>
struct RBTreeNode
{
RBTreeNode(const pair<K, V>&kv)
:_left(nullptr)
, _right(nullptr)
, _parent(nullptr)
, _kv(kv)
, _col(RED)
{}
RBTreeNode<K, V> *_left;
RBTreeNode<K, V> *_right;
RBTreeNode<K, V> *_parent;
pair<K, V> _kv;
enum Color _col;
};
template<class K,class V>
class RBTree
{
typedef RBTreeNode<K,V> Node;
public:
void RotateL(Node *parent)//左旋
{
Node *subR = parent->_right;//左旋,p的右边一定不为空
Node *subL = subR->_left;//可能为空
Node *pparent = parent->_parent;
//将subR左侧节点链接到p的右侧
parent->_right = subL;
if (subL != nullptr)
subL->_parent = parent;
//将p链接到subR的左侧
subR->_left = parent;
parent->_parent = subR;
//subR与pp的链接
subR->_parent = pparent;
if (pparent == nullptr)
_root = subR;
else
{
if (pparent->_left == parent)
pparent->_left = subR;
else
pparent->_right = subR;
}
//颜色更改
parent->_col = RED;
subR->_col = BLACK;
}
void RotateR(Node *parent)//右旋
{
Node *subL = parent->_left;
Node *subR = subL->_right;
Node *pparent = parent->_parent;
parent->_left = subR;
if (subR != nullptr)
subR->_parent = parent;
subL->_right = parent;
parent->_parent = subL;
subL->_parent = pparent;
if (pparent == nullptr)
_root = subL;
else
{
if (pparent->_left == parent)
pparent->_left = subL;
else
pparent->_right = subL;
}
//颜色更改
parent->_col = RED;
subL->_col = BLACK;
}
pair<Node*, bool> Insert(pair<K, V>&kv)
{
if (_root == nullptr)
{
_root = new Node(kv);
_root->_col = BLACK;
return make_pair(_root, true);
}
//有根节点了
Node *parent = nullptr;
Node *cur = _root;
while (cur)
{
if (kv.first > cur->_kv.first)
{
parent = cur;
cur = cur->_right;
}
else if (kv.first < cur->_kv.first)
{
parent = cur;
cur = cur->_left;
}
else//相等,,去重
{
return make_pair(cur, false);
}
}
//此时进行节点的插入
cur = new Node(kv);
Node* newnode = cur;//保存一份,返回用
if (parent->_kv.first > kv.first)//在左边
{
parent->_left = cur;
cur->_parent = parent;
}
else//在右边
{
parent->_right = cur;
cur->_parent = parent;
}
//插入红色的节点,维护规则-》相邻节点不能同样是红色
while (parent&&parent->_col == RED)//父亲节点不为空,并且为红色,说明此时需要进行调整
{
Node *grandfather = parent->_parent;//父亲节点存在且为红色,那么一定不是根节点
Node *uncle = grandfather->_right;
if (grandfather->_right == parent)//父亲节点为右,则叔叔节点为左
uncle = grandfather->_left;
if (uncle != nullptr&&uncle->_col == RED)//情况1:叔叔节点存在且为红色
{
//颜色更改
parent->_col = BLACK;
uncle->_col = BLACK;
grandfather->_col = RED;
//继续向上判断
cur = grandfather;//新的红节点
parent = cur->_parent;//
}
else//叔叔节点不存在,或者存在为黑色
{
if (grandfather->_left == parent)//p在g的左侧
{
if (cur == parent->_left)//c在p的左侧,只需要进行右旋
{
RotateR(grandfather);
}
else//c在p的右侧,先左再右
{
RotateL(parent);
RotateR(grandfather);
}
}
else//p在g的右侧
{
if (cur == parent->_right)//c在p的右侧,左旋
{
RotateL(grandfather);
}
else//先右再左旋
{
RotateR(parent);
RotateL(grandfather);
}
}
break;//旋转之后即完成了要求,不需要再进行判断
}
}
_root->_col = BLACK;//防止根节点被改成红色,根节点赋予黑色,每条路径上都是适用的
return make_pair(newnode, true);
}
//[]重载
V &operator [](const K &k)//string、int、vector等等都可以是V,是由默认的构造函数的 int()=0
{
//insert返回的是pair<node*,bool>
return ((Insert(make_pair(k, V())).first)->_kv).second;
}
//检测相关
//遍历
void _Inorder(Node *root)
{
if (root == nullptr)
return;
_Inorder(root->_left);
cout << root->_kv.first << " " << root->_kv.second <<" "<<root->_col<< endl;
_Inorder(root->_right);
}
void Inorder()
{
_Inorder(_root);
}
//判断是否是红黑树 ->判断一个红色节点的左右子树是否是红色的 -> 判断一个红色节点的父亲是否是红色的
bool CheckCol(Node* root)
{
if (root == nullptr)
return true;
if (root->_col == RED)//当前节点为红色
{
if (root->_parent != nullptr)
{
if (root->_parent->_col == RED)//红色节点的父亲也为红色,则不是红黑树
{
cout << root->_kv.first << " " << root->_kv.second <<"颜色判断失败 ->不是红黑树"<< endl;
return false;
}
}
}
return CheckCol(root->_left) && CheckCol(root->_right);
}
bool CheckBlack(Node *root,int TrueNum,int BlackNum)//统计路径上面的黑色节点
{
if (root == nullptr)//表示一条路径走到底了
{
return TrueNum == BlackNum;//判断每条路径的黑色节点是否相等
}
if (root->_col == BLACK)
BlackNum++;
return
CheckBlack(root->_left, TrueNum, BlackNum) &&
CheckBlack(root->_right, TrueNum, BlackNum);
}
bool Check()
{
Node *cur = _root;
int TrueNum = 0;
if (_root&&_root->_col == RED)//根不能为红色
{
return false;
}
while (cur)//统计一条路径上面的黑色节点的个数
{
if (cur->_col == BLACK)
TrueNum++;
cur = cur->_left;
}
return CheckCol(_root) && CheckBlack(_root, TrueNum, 0);
}
private:
Node *_root = nullptr;
};
#include "rbt.hpp"
#include <vector>
void test1(vector<int>&arr)
{
RBTree<int, int> t;
for (auto&e : arr)
{
t[e]++;
}
t.Inorder();
cout << "_____校验________" << endl;
if (t.Check())
cout << "是红黑树" << endl;
else
cout << "不是红黑树" << endl;
}
int main()
{
cout << "测试1" << endl;
vector<int>arr1 = { 16, 3, 7, 11, 9, 26, 18, 14, 15 };
test1(arr1);
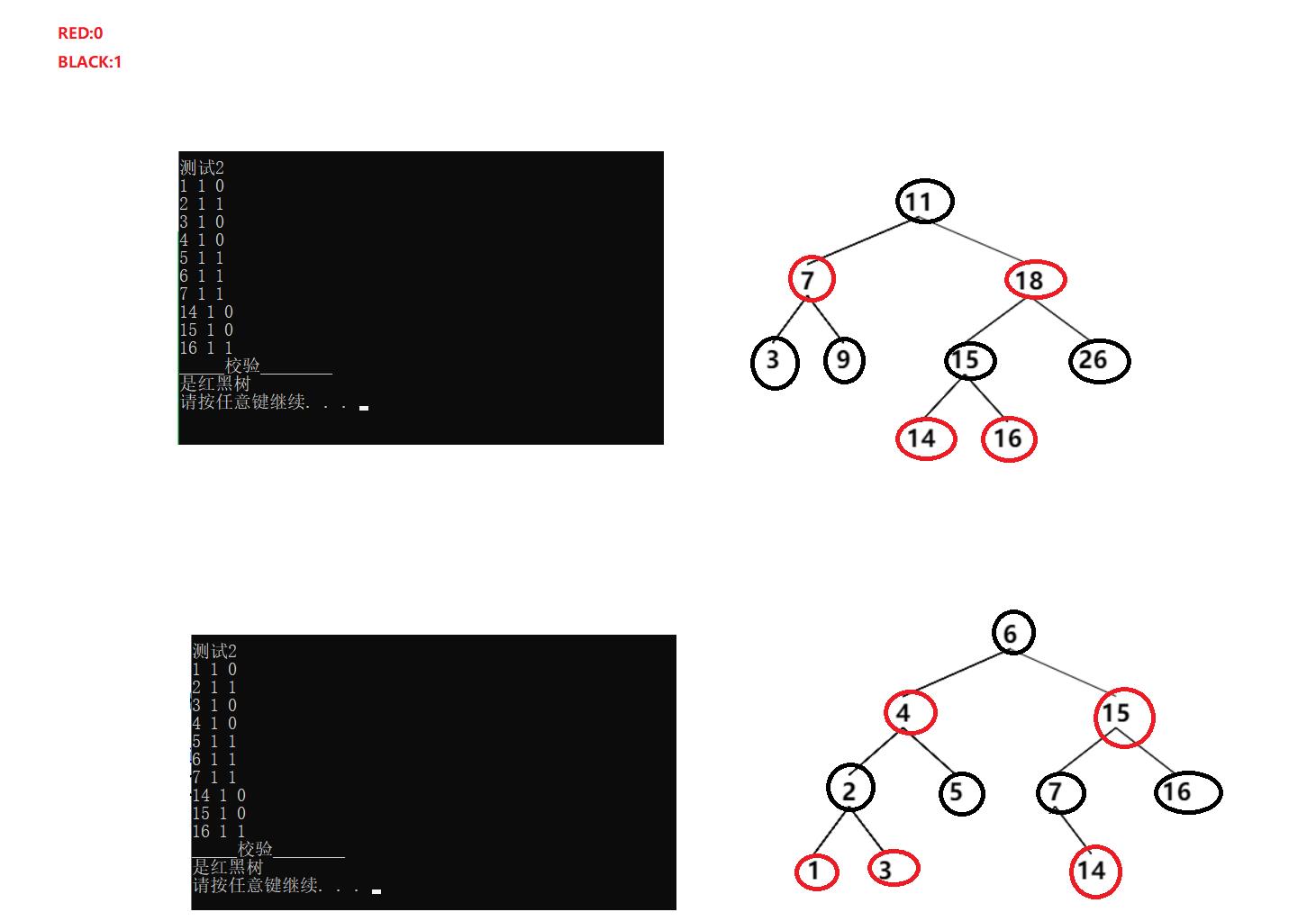
cout << endl << "测试2" << endl;
vector<int>arr2 = { 4, 2, 6, 1, 3, 5, 15, 7, 16, 14 };
test1(arr2);
system("pause");
return 0;
}
3.2验证
4.map、set的封装
4.1原码查看分析

4.2构造思路
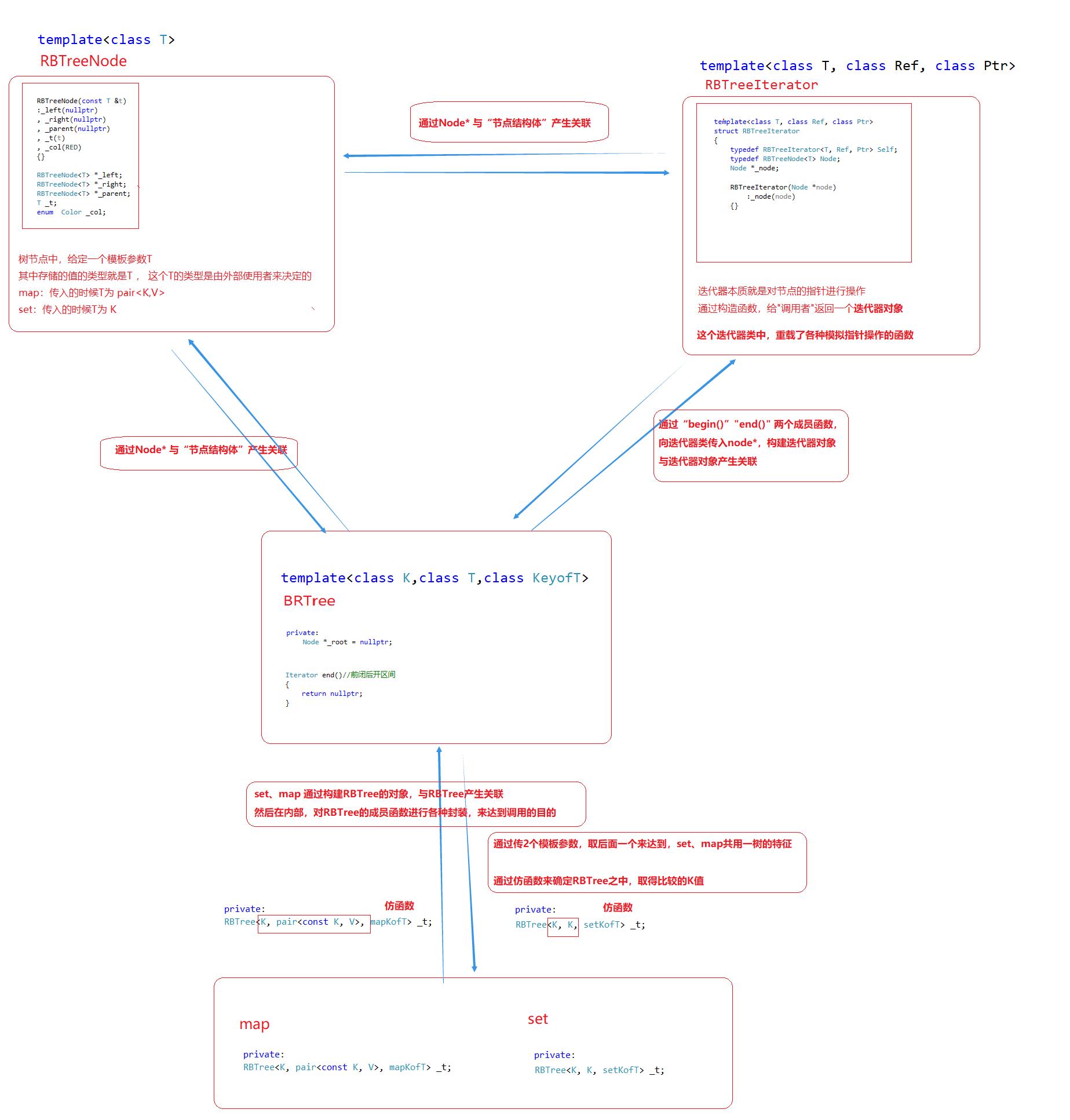
4.3迭代器++、–的构造

4.4代码实现
#pragma once
#include <iostream>
#include <assert.h>
#include <windows.h>
using namespace std;
enum Color
{
RED,
BLACK
};
template<class T>//节点只提供一个T(V)值,构成set和map共用一颗红黑树
struct RBTreeNode
{
RBTreeNode(const T &t)
:_left(nullptr)
, _right(nullptr)
, _parent(nullptr)
, _t(t)
, _col(RED)
{}
RBTreeNode<T> *_left;
RBTreeNode<T> *_right;
RBTreeNode<T> *_parent;
T _t;
enum Color _col;
};
//迭代器的封装
template<class T, class Ref, class Ptr>
struct RBTreeIterator
{
typedef RBTreeIterator<T, Ref, Ptr> Self;//迭代器++ 还是迭代器
typedef RBTreeNode<T> Node;
Node *_node;
RBTreeIterator(Node *node)
:_node(node)
{}
Ref operator *()
{
assert(_node != nullptr);
return _node->_t;
}
Ptr operator ->()
{
assert(_node != nullptr);
return &(_node->_t);//返回的是节点的指针的引用,编译器优化了一次箭头
}
Self operator ++()//找中序的下一个
{
assert(_node != nullptr);
// 中序的下一个
if (_node->_right)//右节点不为空,下一个位置就为右树的最左节点
{
// 右树的最左节点
Node* cur = _node->_right;
while (cur && cur->_left)
{
cur = cur->_left;
}
_node = cur;
}
else
{
//右边为空,表示以cur->parent为根节点的树,已经访问完毕了
//此时再向上搜寻,cur不是parent的右孩子的父亲节点
Node* cur = _node;
Node* parent = cur->_parent;
while (parent && parent->_right == cur)
{
cur = parent;
parent = parent->_parent;
}
_node = parent;
}
return *this;
}
Self operator ++(int)//后置
{
assert(_node != nullptr);
Self rnode= _node;//隐式类型转换
// 中序的下一个
if (_node->_right)//右节点不为空,下一个位置就为右树的最左节点
{
// 右树的最左节点
Node* cur = _node->_right;
while (cur && cur->_left)
{
cur = cur->_left;
}
_node = cur;
}
else
{
//右边为空,表示以cur->parent为根节点的树,已经访问完毕了
//此时再向上搜寻,cur不是parent的右孩子的父亲节点
Node* cur = _node;
Node* parent = cur->_parent;
while (parent && parent->_right == cur)
{
cur = parent;
parent = parent->_parent;
}
_node = parent;
}
return rnode;
}
Self operator--()
{
if (_node == nullptr)//为最后空节点
{
}
else if (_node->_left != nullptr)
{
_node = _node->_left;
}
else//寻找孩子不是父亲左节点的父亲
{
Node *cur = _node;
Node *parent = cur->_parent;
while (parent&&parent->_left == cur)
{
cur = parent;
parent = cur->_parent;
}
_node = parent;
}
return *this;
}
Self operator--(int)//后置减减
{
Self rnode = _node;
if (_node->_left != nullptr)
{
_node = _node->_left;
}
else//寻找孩子不是父亲左节点的父亲
{
Node *cur = _node;
Node *parent = cur->_parent;
while (parent&&parent->_left == cur)
{
cur = parent;
parent = cur->_parent;
}
_node = parent;
}
return rnode;
}
bool operator!=(const Self &s)const
{
return _node != s._node;
}
bool operator==(const Self &s)const
{
return _node == s._node;
}
};
//set<K> -> RVTree<K,K>
//map<K,V> -> RBTree<K,pair<const K,V>>
template<class K,class T,class KeyofT>
//当T是K的时候,传给节点的就是K-> set,当K是pair的时候,传给节点的时候就是pair ->map
//find需要用K值去查找,如果不写K,set知道k是什么,map并不知道
class RBTree
{
typedef RBTreeNode<T> Node;
public:
typedef RBTreeIterator<T, T&, T*> Iterator;
typedef RBTreeIterator<T, const T&, const T*> ConstIterator;
Iterator begin()//最左边的节点
{
Node *cur = _root;
while (cur&&cur->_left)
{
cur = cur->_left;
}
return cur;//隐式类型转换
}
Iterator end()//前闭后开区间
{
return nullptr;
}
ConstIterator begin() const //最左边的节点
{
Node *cur = _root;
while (cur&&cur->_left)
{
cur = cur->_left;
}
return Iterator(cur);
}
ConstIterator end() const //前闭后开区间
{
return Iterator(nullptr);
}
void RotateL(Node *parent)//左旋
{
Node *subR = parent->_right;//左旋,p的右边一定不为空
Node *subL = subR->_left;//可能为空
Node *pparent = parent->_parent;
//将subR左侧节点链接到p的右侧
parent->_right = subL;
if (subL != nullptr)
subL->_parent = parent;
//将p链接到subR的左侧
subR->_left = parent;
parent->_parent = subR;
//subR与pp的链接
subR->_parent = pparent;
if (pparent == nullptr)
_root = subR;
else
{
if (pparent->_left == parent)
pparent->_left = subR;
else
pparent->_right = subR;
}
//颜色更改
parent->_col = RED;
subR->_col = BLACK;
}
void RotateR(Node *parent)//右旋
{
Node *subL = parent->_left;
Node *subR = subL->_right;
Node *pparent = parent->_parent;
parent->_left = subR;
if (subR != nullptr)
subR->_parent = parent;
subL->_right = parent;
parent->_parent = subL;
subL->_parent = pparent;
if (pparent == nullptr)
_root = subL;
else
{
if (pparent->_left == parent)
pparent->_left = subL;
else
pparent->_right = subL;
}
//颜色更改
parent->_col = RED;
subL->_col = BLACK;
}
pair<Node*, bool> Insert(const T &t)
{
KeyofT kot;
if (_root == nullptr)
{
_root = new Node(t);
_root->_col = BLACK;
return make_pair(_root, true);
}
//有根节点了
Node *parent = nullptr;
Node *cur = _root;
while (cur)
{
if (kot(cur->_t) < kot(t))//往右边走
{
parent = cur;
cur = cur->_right;
}
else if (kot(cur->_t) > kot(t))//往左边走
{
parent = cur;
cur = cur->_left;
}
else//相等,,去重
{
return make_pair(cur, false);
}
}
//此时进行节点的插入
cur = new Node(t);
Node* newnode = cur;//保存一份,返回用
if (kot(parent->_t) > kot(t))//在左边
{
parent->_left = cur;
cur->_parent = parent;
}
else//在右边
{
parent->_right = cur;
cur->_parent = parent;
}
//插入红色的节点,维护规则-》相邻节点不能同样是红色
while (parent&&parent->_col == RED)//父亲节点不为空,并且为红色,说明此时需要进行调整
{
Node *grandfather = parent->_parent;//父亲节点存在且为红色,那么一定不是根节点
Node *uncle = grandfather->_right;
if (grandfather->_right == parent)//父亲节点为右,则叔叔节点为左
uncle = grandfather->_left;
if (uncle != nullptr&&uncle->_col == RED)//情况1:叔叔节点存在且为红色
{
//颜色更改
parent->_col = BLACK;
uncle->_col = BLACK;
grandfather->_col = RED;
//继续向上判断
cur = grandfather;//新的红节点
parent = cur->_parent;//
}
else//叔叔节点不存在,或者存在为黑色
{
if (grandfather->_left == parent)//p在g的左侧
{
if (cur == parent->_left)//c在p的左侧,只需要进行右旋
{
RotateR(grandfather);
}
else//c在p的右侧,先左再右
{
RotateL(parent);
RotateR(grandfather);
}
}
else//p在g的右侧
{
if (cur == parent->_right)//c在p的右侧,左旋
{
RotateL(grandfather);
}
else//先右再左旋
{
RotateR(parent);
RotateL(grandfather);
}
}
break;//旋转之后即完成了要求,不需要再进行判断
}
}
_root->_col = BLACK;//防止根节点被改成红色,根节点赋予黑色,每条路径上都是适用的
return make_pair(newnode, true);
}
//[]重载
Iterator operator[] (const T &t)//string、int、vector等等都可以是V,是由默认的构造函数的 int()=0
{
//insert返回的是pair<node*,bool>
return Insert(t).first;//返回node*的迭代器
}
private:
Node *_root = nullptr;
};
#pragma once
#include "rbt.hpp"
namespace my
{
template<class K,class V>
class map
{
struct mapKofT//map作为上层,知道V是什么类型
{
const K& operator ()(const pair<const K, V> &kv)
{
return kv.first;
}
};
public:
typedef typename RBTree<K, pair<const K, V>, mapKofT>::Iterator iterator;
iterator begin()
{
return _t.begin();
}
iterator end()
{
return _t.end();
}
pair<RBTreeNode<pair<const K, V>>*, bool> insert(const pair<const K, V> &kv)
{
return _t.Insert(kv);
}
V& operator[](const K &k)
{
//方法1:
//inser 返回pair<RBTreeNode<pair<const K, V>>*, bool>
//return ((insert(make_pair(k, V())).first)->_t).second;
//方法2:
//_t[]返回一个迭代器
return _t[make_pair(k,V())]->second;
}
private:
RBTree<K, pair<const K, V>, mapKofT> _t;
};
};
#pragma once
#include "rbt.hpp"
namespace my
{
template<class K>
class set
{
struct setKofT//仿函数
{
const K& operator ()(const K &k)
{
return k;
}
};
public:
//typename告诉编译器实例化之后再去找
//如果不加,这里对Iterator进行类型重定义,但是RBTree没有实例化,因此是找不到的
typedef typename RBTree<K, K, setKofT>::Iterator iterator;
iterator begin()//实际上调用的是红黑树的begin
{
return _t.begin();
}
iterator end()
{
return _t.end();
}
pair<RBTreeNode<K>*, bool> insert(const K &k )
{
return _t.Insert(k);
}
private:
RBTree<K, K, setKofT> _t;//红黑树对象
};
};
#include "rbt.hpp"
#include "map.h"
#include "set.h"
#include <string>
void test_map()//map测试
{
my::map<int, int> mp;
mp.insert(make_pair(1, 1));
mp.insert(make_pair(2, 2));
mp.insert(make_pair(3, 2));
mp[2]++;
mp[3]++;
mp[4]++;
mp[5]++;
mp[1]++;
mp[8]++;
mp[9]++;
my::map<int, int>::iterator it = mp.begin();
while (it != mp.end())
{
cout << it->first << " " << it->second << endl;
it++;
}
}
void test_set()
{
my::set<string> st;
st.insert("苹果");
st.insert("香蕉");
st.insert("菠萝");
st.insert("樱桃");
st.insert("哈密瓜");
st.insert("西瓜");
my::set<string>::iterator it = st.begin();
while (it !=st.end())
{
cout << *it << endl;
it++;
}
}
int main()
{
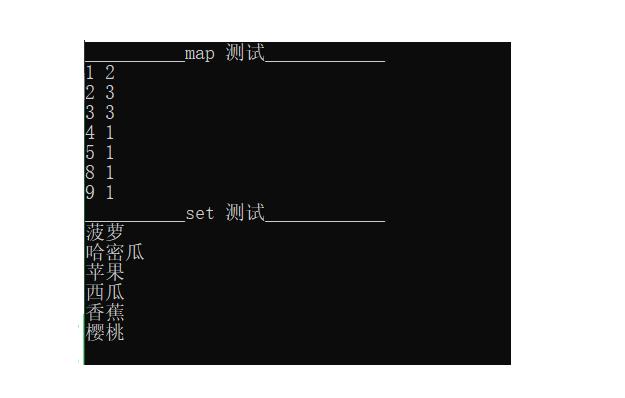
cout << "__________map 测试____________" << endl;
test_map();
cout << "__________set 测试____________" << endl;
test_set();
return 0;
}
4.5测试结果
以上是关于红黑树的实现mapset的封装的主要内容,如果未能解决你的问题,请参考以下文章