LeetCode1310. 子数组异或查询 / 307. 区域和检索 - 数组可修改（线段树树状数组）

Posted 2021-06-21 Zephyr丶J

1310. 子数组异或查询

2021.5.12每日一题

题目描述

有一个正整数数组 arr，现给你一个对应的查询数组 queries，其中 queries[i] = [Li, Ri]。

对于每个查询 i，请你计算从 Li 到 Ri 的 XOR 值（即 arr[Li] xor arr[Li+1] xor ... xor arr[Ri]）作为本次查询的结果。

并返回一个包含给定查询 queries 所有结果的数组。

示例 1：

输入：arr = [1,3,4,8], queries = [[0,1],[1,2],[0,3],[3,3]]
输出：[2,7,14,8] 
解释：
数组中元素的二进制表示形式是：
1 = 0001 
3 = 0011 
4 = 0100 
8 = 1000 
查询的 XOR 值为：
[0,1] = 1 xor 3 = 2 
[1,2] = 3 xor 4 = 7 
[0,3] = 1 xor 3 xor 4 xor 8 = 14 
[3,3] = 8
示例 2：

输入：arr = [4,8,2,10], queries = [[2,3],[1,3],[0,0],[0,3]]
输出：[8,0,4,4]

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/xor-queries-of-a-subarray
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

思路

简简单单前缀

class Solution {
    public int[] xorQueries(int[] arr, int[][] queries) {
        //直接异或吧，这有什么好办法吗，感觉不到啊，难道也是前缀？
        //好像真的前缀可以,然后求对应的queries中的值
        int l = arr.length;
        int[] pre = new int[l + 1];
        for(int i = 1; i <= l; i++){
            pre[i] = pre[i - 1] ^ arr[i - 1];
        }

        int n = queries.length;
        int[] res = new int[n];
        for(int i = 0; i < n; i++){
            int left = queries[i][0];
            int right = queries[i][1];
            res[i] = pre[left] ^ pre[right + 1];
        }
        return res;
    }
}

本来觉得这道题就这么结束了，结果看了一下三叶姐的题解，发现用了一个树状数组，而树状数组是针对区间内数字可以修改的求区间和问题准备的，没错，又发现新的东西了，马不停蹄去看看，然后又发现了线段树，学

307. 区域和检索 - 数组可修改

题目描述

给你一个数组 nums ，请你完成两类查询，其中一类查询要求更新数组下标对应的值，另一类查询要求返回数组中某个范围内元素的总和。

实现 NumArray 类：

NumArray(int[] nums) 用整数数组 nums 初始化对象
void update(int index, int val) 将 nums[index] 的值更新为 val
int sumRange(int left, int right) 返回子数组 nums[left, right] 的总和（即，nums[left] + nums[left + 1], ..., nums[right]）
 

示例：

输入：
["NumArray", "sumRange", "update", "sumRange"]
[[[1, 3, 5]], [0, 2], [1, 2], [0, 2]]
输出：
[null, 9, null, 8]

解释：
NumArray numArray = new NumArray([1, 3, 5]);
numArray.sumRange(0, 2); // 返回 9 ，sum([1,3,5]) = 9
numArray.update(1, 2);   // nums = [1,2,5]
numArray.sumRange(0, 2); // 返回 8 ，sum([1,2,5]) = 8

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/range-sum-query-mutable
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

思路

这道题因为数组中的元素可以改变，因此不能用简单的前缀和的方法了
因为三叶姐也没说树状数组具体是啥东西，所以只能先看官解的线段树

线段树

其实也好理解，首先是一个二叉树，叶子结点是数组中每个元素的值，然后它们的父节点就是两个结点的值相加，得到一个区间的和。

线段树有三个关键点，第一是构建线段树，第二是修改元素的时候要更新线段树，第三是根据线段树进行区域和的检索

具体实现起来呢，假设一个数组有n个数，那么这样的树结点数就有2n - 1 个，因此创建一个长度为2n的数组，并把数组中的数放到整个数组的后n位中
然后对于其他节点，根据tree[i] = tree[i * 2] + tree[2 * i + 1] 计算剩下结点的值，到这里，构建了一个颗线段树

要更新数组中下标 i 对应的元素，对应的包含这个元素的区间都要进行更新
先更新tree[i + n]，因为线段树的tree[i] = tree[i * 2] + tree[2 * i + 1] 可知，左边结点的下标是偶数，右边是奇数，因此，根据(i + n)的奇偶性进行更新，如果是偶数，那么就用tree[i + n]和tree[i + n + 1]更新tree[(i + n)/2]；如果是奇数，用tree[i + n - 1]和tree[i + n]更新tree[(i + n)/2]，然后一直往上更新，知道下标越界

查询区间和，给定一个区间 [i, j] , 同样因为 tree[i] = tree[i * 2] + tree[2 * i + 1]， 如果左边界在右结点，那么需要单独加这个结点，并且越过这个结点即i++（如果直接找父节点的话，会多加一个值）；同样，如果右边界在左节点，同样需要单独加这个结点，同时j–
然后，整体的逻辑就是不断地找向上找，i / 2， j / 2，直到左右边界相遇，就找到了一个区间，再加上特殊处理的值，最终就是区间和

理解了代码其实并不难写

class NumArray {
    int[] tree;
    int n;
    //线段树有三个关键点，第一是构建线段树，第二是修改元素的时候要更新线段树，第三是根据线段树进行区域和的检索
    public NumArray(int[] nums) {
        n = nums.length;
        tree = new int[2 * n];
        //后n个
        for(int i = n; i < 2 * n; i++){
            tree[i] = nums[i - n];
        }
        for(int i = n - 1; i > 0; i--){
            tree[i] = tree[2 * i] + tree[2 * i + 1];
        }
    }
    
    public void update(int index, int val) {
        //tree中的下标
        int id = index + n;
        tree[id] = val;
        while(id > 0){
            if(id % 2 == 0){
                tree[id / 2] = tree[id] + tree[id + 1];
            }else{
                tree[id / 2] = tree[id - 1] + tree[id];
            }
            id /= 2;
        }
    }
    
    public int sumRange(int left, int right) {
        //区间和
        int sum = 0;
        int left_tree = left + n;
        int right_tree = right + n;
        //这里注意要写成小于等于
        while(left_tree <= right_tree){
            if(left_tree % 2 == 1){
                sum += tree[left_tree];
                left_tree++;
            }
            if(right_tree % 2 == 0){
                sum += tree[right_tree];
                right_tree--;
            }
            right_tree /= 2;
            left_tree /= 2;
        }
        return sum;
    }
}

再来看看树状数组

树状数组

首先给出模板

// 上来先把三个方法写出来
{
    int[] tree;
    int lowbit(int x) {
        return x & -x;
    }
    // 查询前缀和的方法
    int query(int x) {
        int ans = 0;
        for (int i = x; i > 0; i -= lowbit(i)) ans += tree[i];
        return ans;
    }
    // 在树状数组 x 位置中增加值 u
    void add(int x, int u) {
        for (int i = x; i <= n; i += lowbit(i)) tree[i] += u;
    }
}

// 初始化「树状数组」，要默认数组是从 1 开始
{
    for (int i = 0; i < n; i++) add(i + 1, nums[i]);
}

// 使用「树状数组」：
{   
    void update(int i, int val) {
        // 原有的值是 nums[i]，要使得修改为 val，需要增加 val - nums[i]
        add(i + 1, val - nums[i]); 
        nums[i] = val;
    }
    
    int sumRange(int l, int r) {
        return query(r + 1) - query(l);
    }
}

作者：AC_OIer
链接：https://leetcode-cn.com/problems/range-sum-query-mutable/solution/guan-yu-ge-lei-qu-jian-he-wen-ti-ru-he-x-41hv/
来源：力扣（LeetCode）
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

我先自己根据三叶姐写的模板代码推了一下，假设五个数[u,t,m,n,x]

这里首先要理解一个操作，就是x & -x， 这个是什么意思呢，因为计算机中负数是以补码的形式存储的，而求一个数的补码，就是这个数二进制位取反再加1，因此可以举几个例子想一想，取反以后x与-x所有位置都是相反的，而此时加1，-x此时从右到左第一个0变成1，后面都变成了0；再做x & -x， 即可以得到原x中最低位的1

知道了这个操作的意思以后，一步步模拟构建这棵树的操作
第一轮循环
tree[1] = u, tree[2] = u, tree[4] = u
第二轮循环
tree[2] = u + t, tree[4] = u + t
第三轮循环
tree[3] = m，tree[4] = u + t + m
第四轮循环
tree[4] = u + t + m + n
第五轮循环
tree[5] = x

这样模拟还是找不到头绪，因此只能去看树状数组的结构（图源：https://blog.csdn.net/qq_34990731/article/details/82889654）

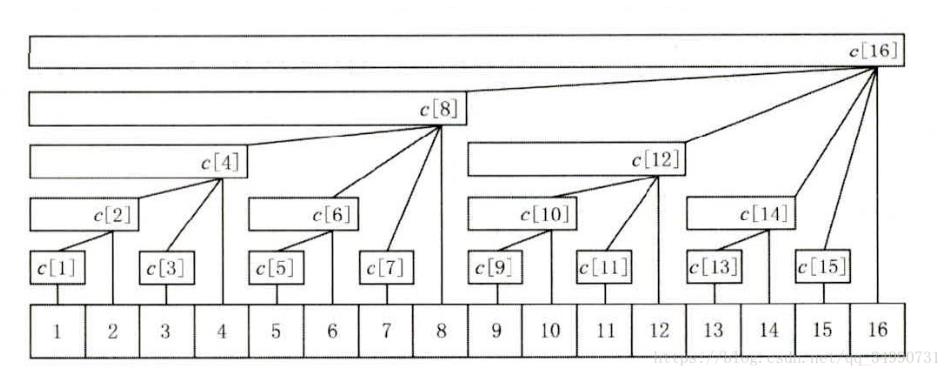
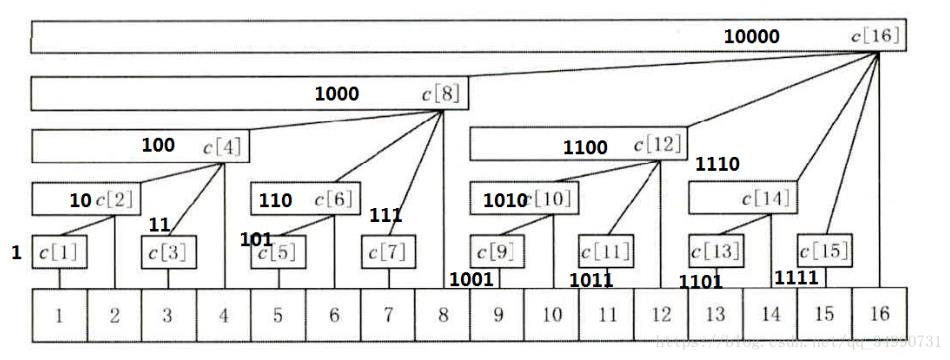
看这张图，可以发现：（重点）
第一：设节点编号为x，那么这个节点管辖的区间为2^k（其中k为x二进制末尾0的个数）个元素；
第二：二进制末尾0的个数，也表示该结点的层数，0个表示在最底层，1个表示在第一层，例如16，二进制末尾3个0，表示编号16的结点在第三层
第三：对于处于数组位置 i 的结点，其代表的信息区间为 [i - lowbit(i) + 1, i]
第四：设当前结点编号为x，从子节点到父节点，可以通过x + lowbit(x)计算得到父节点的编号，例如编号为9时，最大编号为16，计算得到的值为10,12,16；可以通过这个规律来更新结点的值
第五：通过树状数组来计算前缀和，可以通过计算与当前结点同层的，并比它小的所有节点（称为兄弟结点）的和得到；例如，计算下标（1,14）的和，那么即计算结点14,12,8的和
第六：如何通过当前结点的下标，计算兄弟结点的下标：x - lowbit(x)
第七：更新结点时，它的所有父节点要同时更新，且x是更新前后的差值

class NumArray {
    //树状数组来咯
    int[] tree;
    int lowbit(int x){
        return x & -x;
    }
    void add(int idx, int x){
        for(int i = idx; i <= n; i += lowbit(i)){
            tree[i] += x;
        }
    }

    int query(int idx){
        int res = 0;
        for(int i = idx; i > 0; i -= lowbit(i)){
            res += tree[i];
        }
        return res;
    }

    int n;
    int[] nums;
    public NumArray(int[] nums) {
        n = nums.length;
        this.nums = nums;
        tree = new int[n + 1];
        for(int i = 0; i < n; i++){
            add(i + 1, nums[i]);
        }
    }
    
    public void update(int index, int val) {
        //在原有数字基础上加上差值
        int cha = val - nums[index];
        add(index + 1, cha);
        nums[index] = val;
    }
    
    public int sumRange(int left, int right) {
        return query(right + 1) - query(left);
    }
}

/**
 * Your NumArray object will be instantiated and called as such:
 * NumArray obj = new NumArray(nums);
 * obj.update(index,val);
 * int param_2 = obj.sumRange(left,right);
 */