LeetCode1738. 找出第 K 大的异或坐标值（快排堆排序）/ 剑指 Offer 48. 最长不含重复字符的子字符串 / 剑指 Offer 49. 丑数

Posted 2021-06-21 Zephyr丶J

1738. 找出第 K 大的异或坐标值

2021.5.19每日一题

题目描述

给你一个二维矩阵 matrix 和一个整数 k ，矩阵大小为 m x n 由非负整数组成。

矩阵中坐标 (a, b) 的 值 可由对所有满足 0 <= i <= a < m 且 0 <= j <= b < n 的元素 matrix[i][j]（下标从 0 开始计数）执行异或运算得到。

请你找出 matrix 的所有坐标中第 k 大的值（k 的值从 1 开始计数）。


示例 1：

输入：matrix = [[5,2],[1,6]], k = 1
输出：7
解释：坐标 (0,1) 的值是 5 XOR 2 = 7 ，为最大的值。
示例 2：

输入：matrix = [[5,2],[1,6]], k = 2
输出：5
解释：坐标 (0,0) 的值是 5 = 5 ，为第 2 大的值。
示例 3：

输入：matrix = [[5,2],[1,6]], k = 3
输出：4
解释：坐标 (1,0) 的值是 5 XOR 1 = 4 ，为第 3 大的值。
示例 4：

输入：matrix = [[5,2],[1,6]], k = 4
输出：0
解释：坐标 (1,1) 的值是 5 XOR 2 XOR 1 XOR 6 = 0 ，为第 4 大的值。

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/find-kth-largest-xor-coordinate-value
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

思路

吐槽一下，“可由”这两个字用的很迷惑，到底是“由”还是“可以由”呢，按正常理解应该是“可以由”，但是看下面的例子，都是“由”，所以先按“由”来做吧

“由”的话就很简单了，相当于求二维数组的前缀和，秒了

class Solution {
    public int kthLargestValue(int[][] matrix, int k) {
        //按“由”来做的话，就简单起来了，相当于二维数组的前缀和
        //然后将所有计算得到的数放在一个大根堆中，弹出k个就是答案
        int m = matrix.length;
        int n = matrix[0].length;

        int[][] pre = new int[m + 1][n + 1];

        PriorityQueue<Integer> pq = new PriorityQueue<>((a, b) -> (b - a));
        for(int i = 1; i <= m; i++){
            for(int j = 1; j <= n; j++){
                pre[i][j] = pre[i - 1][j] ^ pre[i][j - 1] ^ pre[i - 1][j - 1] ^ matrix[i - 1][j - 1];
                pq.offer(pre[i][j]);
            }
        }

        int res = 0;
        for(int i = 0; i < k; i++){
            res = pq.poll();
        }
        return res;
    }
}

题解中对排序这里，使用的是基于快排思想的选择策略，和前几天做的剑指offer中提到好几次的方法是一样的
因为快排每次都是确定一个数在数组中的位置，因此如果这个位置小于k，那么就再递归调用右边，这个位置大于k，递归调用左边

然后写了一下，因为要找第k 个最大值，所以很自然的想把快排改成从大到小排序，（当前也可以从小到大排但是从右往左找）在选i还是j的时候纠结了一下，然后发现最终退出的时候，i和j肯定是相同的，所以也不需要纠结，但是超时了，这是我万万没有想到的

class Solution {
    public int kthLargestValue(int[][] matrix, int k) {
        //按“由”来做的话，就简单起来了，相当于二维数组的前缀和
        //然后将所有计算得到的数放在一个大根堆中，弹出k个就是答案
        int m = matrix.length;
        int n = matrix[0].length;

        int[][] pre = new int[m + 1][n + 1];

        List<Integer> list = new ArrayList<>();
        for(int i = 1; i <= m; i++){
            for(int j = 1; j <= n; j++){
                pre[i][j] = pre[i - 1][j] ^ pre[i][j - 1] ^ pre[i - 1][j - 1] ^ matrix[i - 1][j - 1];
                list.add(pre[i][j]);
            }
        }

        int l = list.size();
        quickSort(list, 0, l - 1, k);
        return list.get(k - 1);
    }

    public void quickSort(List<Integer> list, int left, int right, int k){
        if(left >= right)
            return;
        //这里学习一下用随机取一个下标的方法
        int pivot = (int)(left + Math.random() * (right - left + 1));
        int mid = list.get(pivot);
        swap(list, left, pivot);
        int i = left;
        int j = right;
        
        while(i < j){
            while(i < j && list.get(j) <= mid)
                j--;
            while(i < j && list.get(i) >= mid)
                i++;
            swap(list, i, j);
        }
        //如果正好是k，那么就返回
        swap(list, j, left);
        if(j == k - 1)
            return;

        if(j > k - 1)
            quickSort(list, left, j - 1, k);
        if(j < k - 1)
            quickSort(list, j + 1, right, k);
    }

    public void swap(List<Integer> list, int i, int j){
        int temp = list.get(i);
        list.set(i, list.get(j));
        list.set(j, temp);
    }
}

超时了以后，看到个代码是用数组做的，贴过来一运行，100%，然后我把我的代码改成数组，还是有超时的风险，不懂了，就这样吧，不纠结这个问题了
看了一下官解的三路划分，也没大看懂
还是来复习一下堆排序的写法吧，自从学了以后好像再也没写过堆排序

堆排序

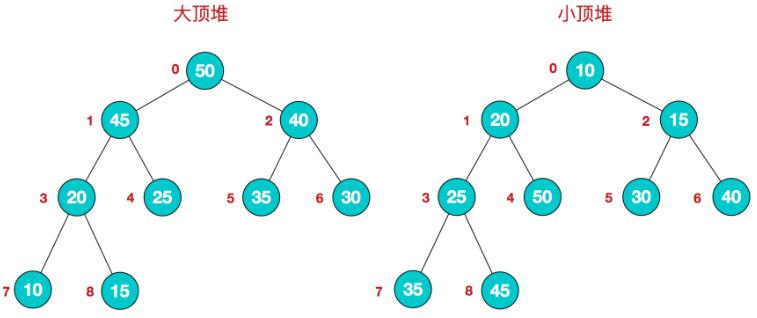
首先，堆是具有以下性质的完全二叉树：每个结点的值都大于或等于其左右孩子结点的值，称为大顶堆；或者每个结点的值都小于或等于其左右孩子结点的值，称为小顶堆。
关键：
大顶堆：arr[i] >= arr[2i+1] && arr[i] >= arr[2i+2]
小顶堆：arr[i] <= arr[2i+1] && arr[i] <= arr[2i+2]

堆排序（从大到小）就是构造一个大顶堆，然后将堆顶元素和末尾元素交换，然后再对n-1个元素重建大顶堆。如此反复的交换、重建、交换、重建，直到n个元素都被处理，就得到了一个排序的数组

借助LeetCode215. 数组中的第K个最大元素，写了一下堆排序的代码，如下：

class Solution {
    public int findKthLargest(int[] nums, int k) {
        //堆排序写一下
        int heapsize = nums.length;
        //先建立大根堆
        buildHeap(nums, heapsize);
        for(int i = 1; i <= k - 1; i++){
            //将最小值和最大值交换
            swap(nums, 0, heapsize - i);
            //调整大根堆
            adjustHeap(nums, 0, heapsize - i);
        }
        return nums[0];

    }

    public void buildHeap(int[] nums, int heapsize){
        //从底部到顶部构建大根堆，找最后一个非叶子结点
        for(int i = heapsize / 2; i >= 0; i--){
            adjustHeap(nums, i, heapsize);
        }
    }

    public void adjustHeap(int[] nums, int i, int heapsize){
        int left = i * 2 + 1;     //左子节点
        int right = i * 2 + 2;    //右子节点
        int max = i;
        //取三个结点的最大值
        if(left < heapsize && nums[left] > nums[max])
            max = left;
        if(right < heapsize && nums[right] > nums[max])
            max = right;
        //如果发生了交换，就继续调整子树
        if(max != i){
            swap(nums, i, max);
            adjustHeap(nums, max, heapsize);
        }
    }

    public void swap(int[] nums, int i, int j){
        int temp = nums[i];
        nums[i] = nums[j];
        nums[j] = temp;
    }
}

剑指 Offer 48. 最长不含重复字符的子字符串

题目描述

请从字符串中找出一个最长的不包含重复字符的子字符串，计算该最长子字符串的长度。


示例 1:

输入: "abcabcbb"
输出: 3 
解释: 因为无重复字符的最长子串是 "abc"，所以其长度为 3。
示例 2:

输入: "bbbbb"
输出: 1
解释: 因为无重复字符的最长子串是 "b"，所以其长度为 1。
示例 3:

输入: "pwwkew"
输出: 3
解释: 因为无重复字符的最长子串是 "wke"，所以其长度为 3。
     请注意，你的答案必须是 子串 的长度，"pwke" 是一个子序列，不是子串。

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/zui-chang-bu-han-zhong-fu-zi-fu-de-zi-zi-fu-chuan-lcof
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

思路

子串，滑动窗口

class Solution {
    public int lengthOfLongestSubstring(String s) {
        //滑动窗口，哈希表存储元素个数
        int l = s.length();
        Set<Character> set = new HashSet<>();
        int max = 0;
        int left = 0;
        for(int i = 0; i < l; i++){
            char c = s.charAt(i);
            //如果已经有这个元素了
            while(set.contains(c)){
                //把这个元素去掉
                char temp = s.charAt(left);
                set.remove(temp);
                left++;
            }
            set.add(c);
            max = Math.max(max, i - left + 1);
        }
        return max;
    }
}

50. Pow(x, n)

题目描述

实现 pow(x, n) ，即计算 x 的 n 次幂函数（即，xn）。


示例 1：

输入：x = 2.00000, n = 10
输出：1024.00000
示例 2：

输入：x = 2.10000, n = 3
输出：9.26100
示例 3：

输入：x = 2.00000, n = -2
输出：0.25000
解释：2-2 = 1/22 = 1/4 = 0.25

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/powx-n
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

思路

今天又有“学习”里面的内容了，所以这里再复习一下这道题，两种方法，分治和二进制
注意这里int类型的n要转换成long

class Solution {
    public double myPow(double x, int n) {
        //用二进制来写一下
        //因为示例中n有-2^31，如果取反，会溢出所以只能先存入long
        long N = n;
        if(N < 0){
            N = -N;
            x = 1 / x; 
        }
        double res = 1.0;
        while(N > 0){
            if((N & 1) == 1){
                res *= x;
            }
            N >>= 1;
            x *= x;
        }
        return res;
    }
}

剑指 Offer 49. 丑数

题目描述

我们把只包含质因子 2、3 和 5 的数称作丑数（Ugly Number）。求按从小到大的顺序的第 n 个丑数。


示例:

输入: n = 10
输出: 12
解释: 1, 2, 3, 4, 5, 6, 8, 9, 10, 12 是前 10 个丑数。

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/chou-shu-lcof
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

思路

为了做三道新题，哈哈
动态规划的思想，因为每个丑数都是由前面的丑数乘以2、3或者5得到的
至于怎么转移呢，用三个指针指向该指针还未处理过的最小的丑数，三个指针分别表示当前数将要乘以2 3 5，那么下一个丑数就是三个指针指向的数分别乘以2 3 5 后得到的最小值
说着有点绕，但是其实还是比较容易理解的

class Solution {
    public int nthUglyNumber(int n) {
        //动态规划吧，刚开始1，然后乘2，得到2，乘3得到3，然后2 * 2 = 4， 1 * 5 = 5
        //2 * 3 = 6； 4 * 2 = 8； 3 * 3 = 9；
        //取三个指针，分别表示2 3 5 三个因子还未处理过的最小数
        int p2 = 1;
        int p3 = 1;
        int p5 = 1;

        //初始化
        int[] dp = new int[n + 1];  
        dp[1] = 1;

        //对于每个丑数，可由前面最小的丑数乘上因子而来
        for(int i = 2; i <= n; i++){
            dp[i] = Math.min(dp[p2] * 2, Math.min(dp[p3] * 3, dp[p5] * 5));
            if(dp[i] == dp[p2] * 2)
                p2++;
            if(dp[i] == dp[p3] * 3)
                p3++;
            if(dp[i] == dp[p5] * 5)
                p5++;
        }
        return dp[n];
    }
}