二叉树

Posted 2021-06-21 L_add

二叉树

二叉树的存储结构

1、顺序存储：用数组来存储，只适用于完全二叉树（堆），因为会存在空间浪费，现实中只有堆才会用数组来存储。二叉树顺序存储在物理上是数组，在逻辑上是一颗二叉树。
2.链式存储：用链表来表示一颗二叉树。

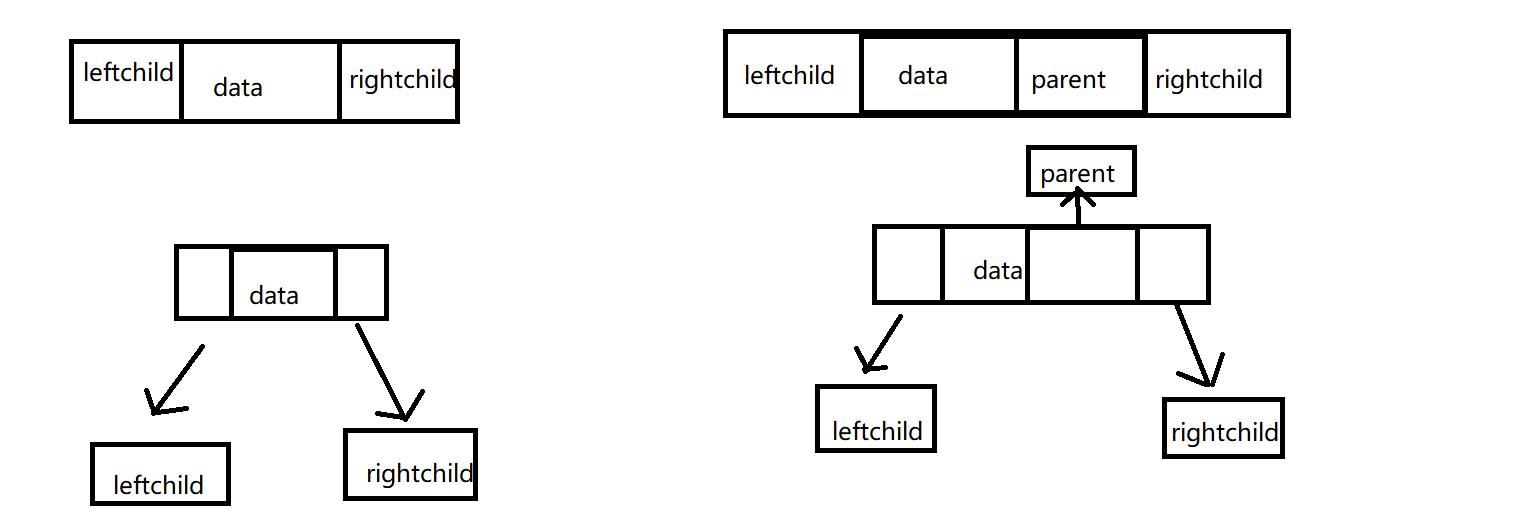
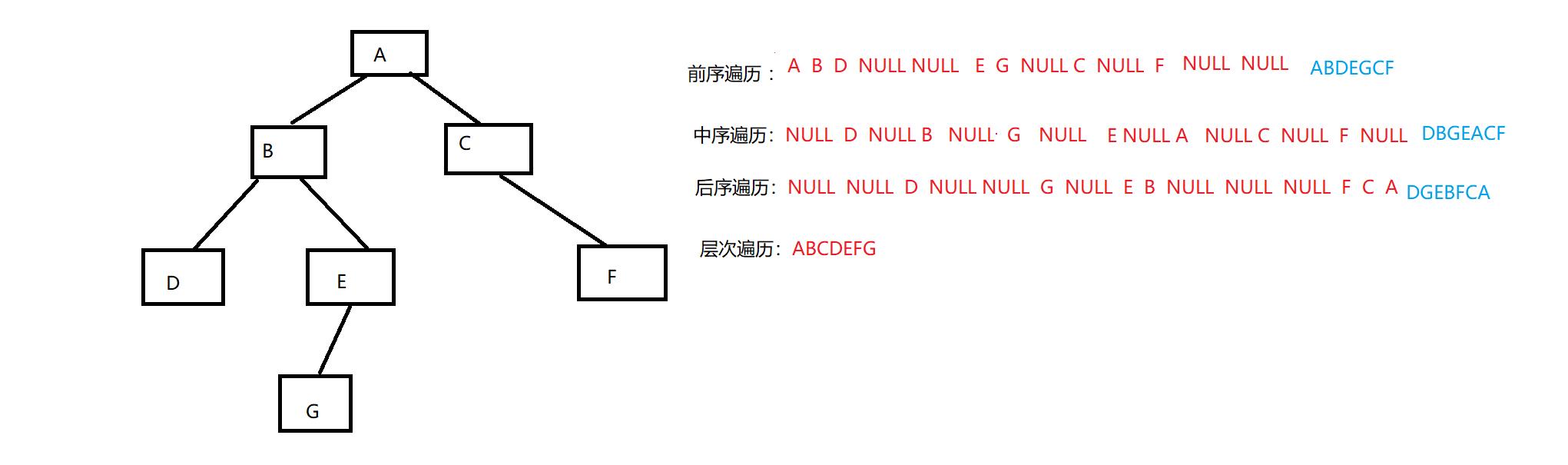
二叉树的遍历

四种遍历顺序：
1、前序遍历 先根遍历 根 -> 左 -> 右
2、中序遍历 中根遍历 左 -> 根 -> 右
3、后序遍历 后根遍历 左 -> 右 -> 根
4、层序遍历

普通二叉树增删查改没有意义，如果是为了存储数据，用线性表更简单，二叉树反而复杂。（极端情况下搜索二叉树退化效率为O(N)）
哈夫曼树：哈夫曼编码 -> 文件压缩
搜索树：AVL树、红黑树(平衡树)

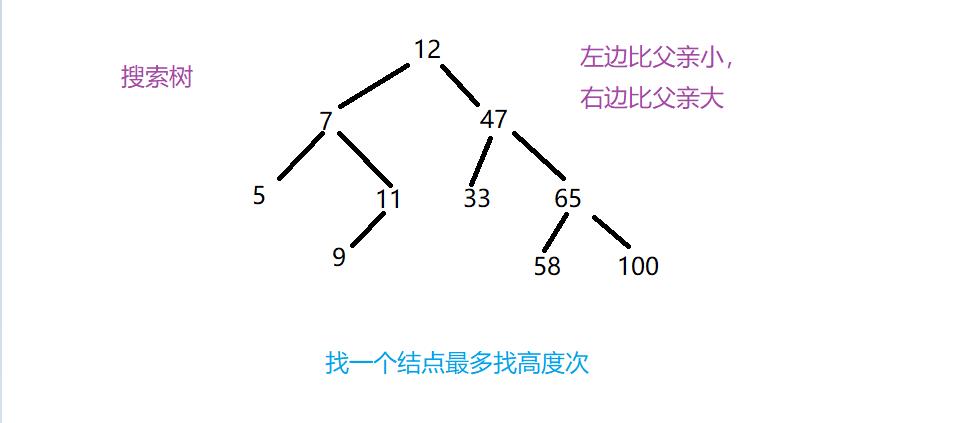
排序二叉树增删查改才有意义

二叉树的实现

1、表示

typedef char BTDataType;
typedef struct BinaryTreeNode
{
	struct BinaryTreeNode* left;
	struct BinaryTreeNode* right;
	BTDataType data;
}BTNode;

2、创建结点

BTNode* CreateTreeNode(BTDataType x)
{
	BTNode* node = (BTNode*)malloc(sizeof(BTNode));
	node->data = x;
	node->left = NULL;
	node->right = NULL;
	return node;

}

3、前、中、后序遍历

递归调用

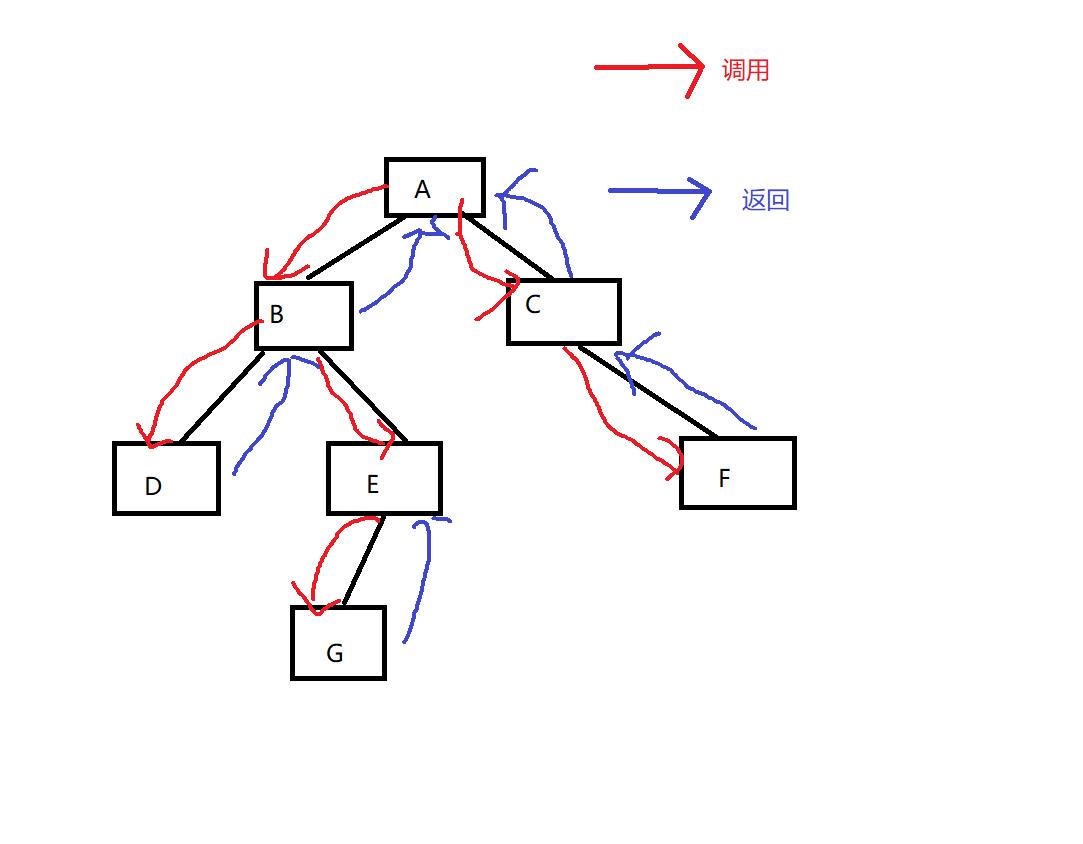
void PrevOrder(BTNode* root)//前序
{
	if (root == NULL)
	{
		printf("NULL");
		return ;
	}
	printf("%c", root->data);
	PrevOrder(root->left);
	PrevOrder(root->right);
}
void InOrder(BTNode* root)//中序
{
	if (root == NULL)
	{
		printf("NULL");
		return;
	}
	InOrder(root->left);
	printf("%c", root->data);
	InOrder(root->right);
}
void PostOrder(BTNode* root)//后序
{
	if (root == NULL)
	{
		printf("NULL");
		return;
	}
	PostOrder(root->left);
	PostOrder(root->right);
	printf("%c", root->data);
}

4、求树结点的个数

int TreeSize(BTNode* root)//树结点的个数
{
	return root == NULL ? 0 : TreeSize(root->left) + TreeSize(root->right) + 1;
}

分治算法：分而治之
把大问题拆成小问题
思路：
1、空 ：返回0；
2、非空 ：左子树结点个数 + 右结点个数 + 1（自己）

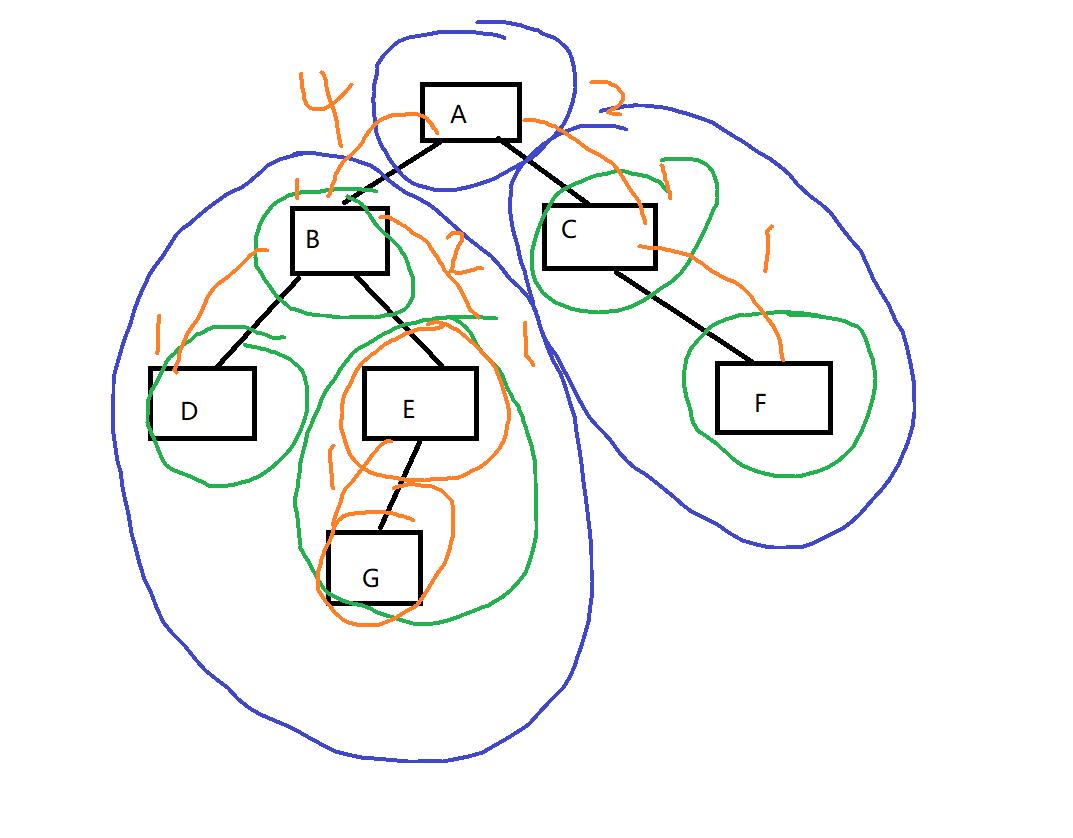
5、求叶子结点个数

思路：
1、空 ：返回0
2、叶子 ：返回1
3、非空且不是叶子 ：返回左子数叶子结点个数+右子树结点个数

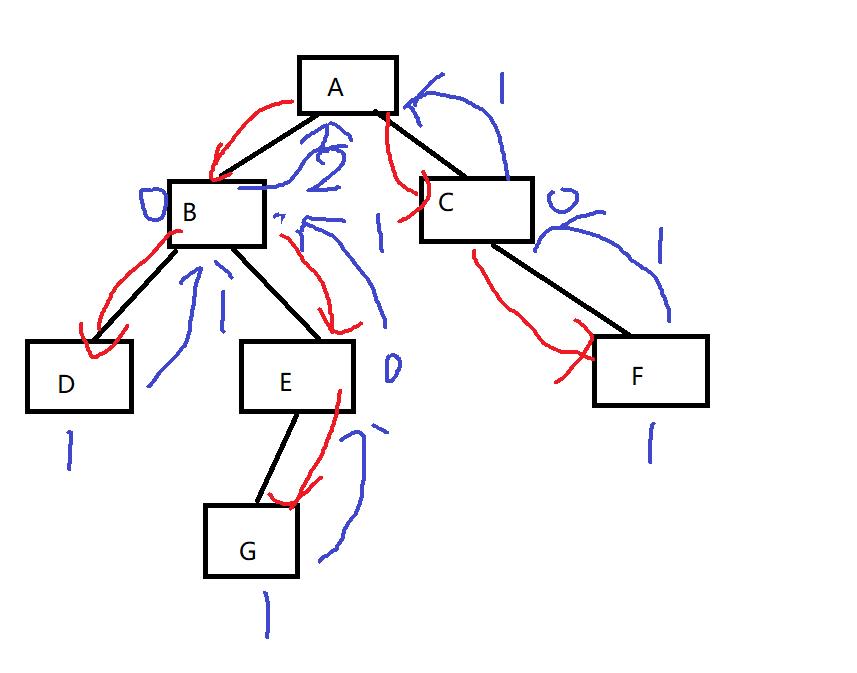
int TreeLeafSize(BTNode* root)//叶子结点的个数
{
	if (root == NULL)
	{
		return 0;
	}
	if (root->left == NULL&& root->right == NULL)
		return 1;
	return TreeLeafSize(root->left) + TreeLeafSize(root->right);
}

7、求第K层叶子结点个数

思路：
求第K层个数，转化为求K-1层个数
K-> K-1 -> K-2 ->… -> 2 -> 1 ->返回个数

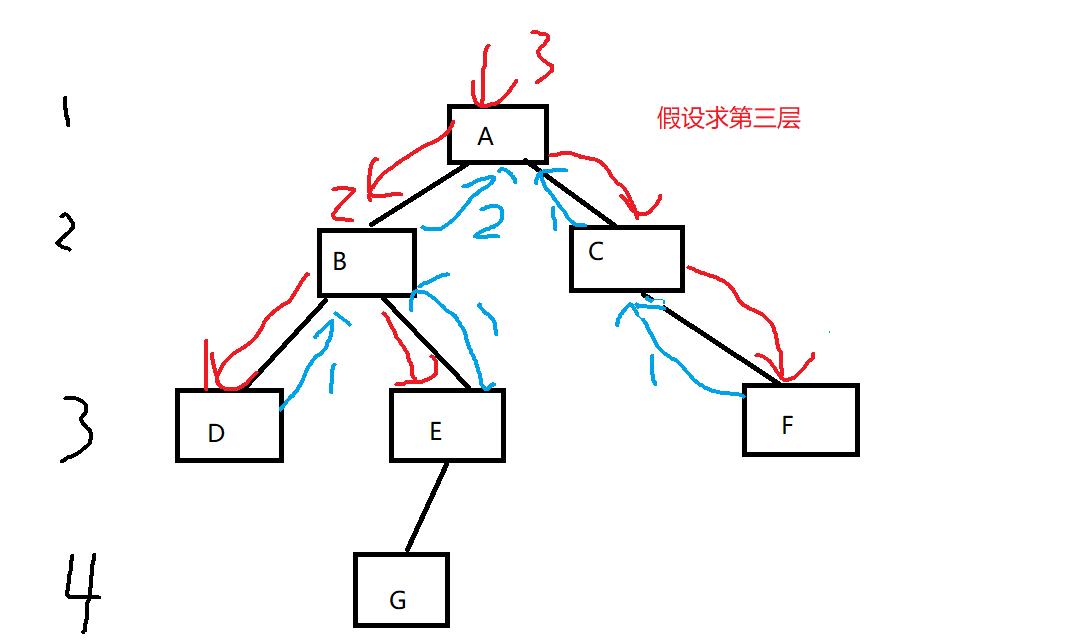
int TreeKLevelSize(BTNode* root, int k)//第K层叶子结点个数
{
	if (root == NULL)
		return 0;
	if (k == 1)
		return 1;
	return TreeKLevelSize(root->left, k - 1) + 
		   TreeKLevelSize(root->right, k - 1);

}

8、找结点

思路：
1、root == NULL return NULL
2、root 结点不是我们要找的，先去左树找，如果左树没有，再到右树找
3、左右都没有，当前树没有，return NULL

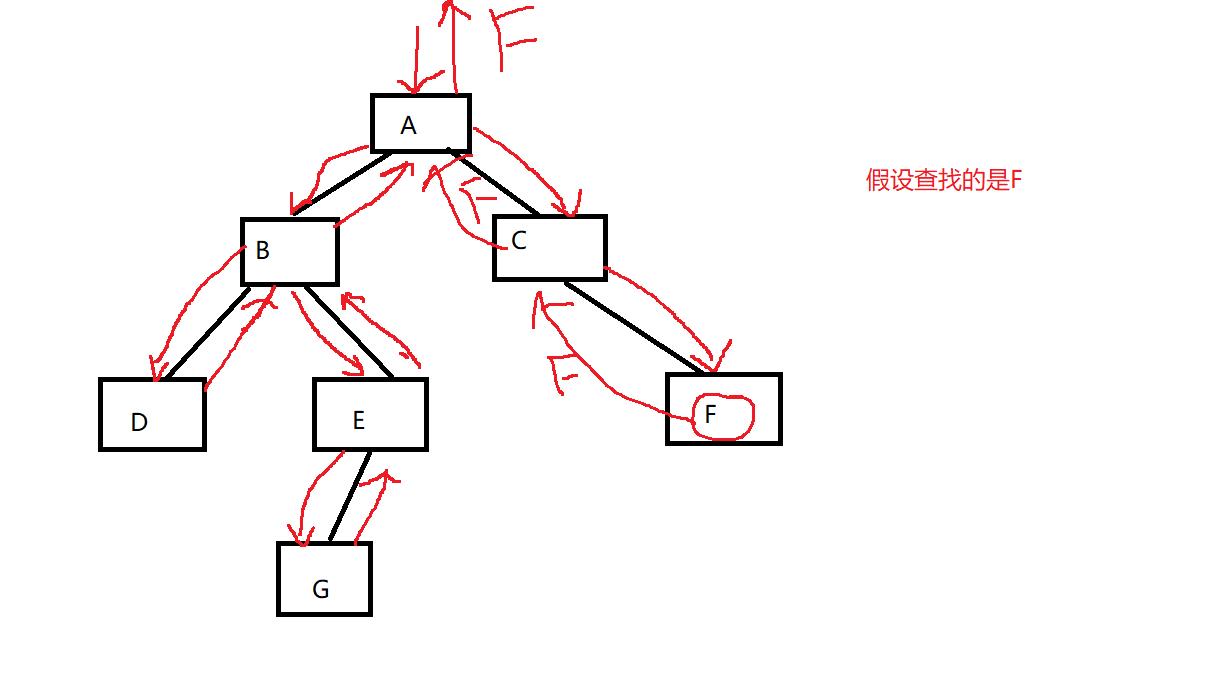
BTNode* TreeFind(BTNode* root, BTDataType x)
{
	if (root == NULL)
		return NULL;
	//我自己不是
	if (root->data == x)
		return root;
	//分别到左右子树寻找
	BTNode* lret = TreeFind(root->left,x);
	if (lret)
		return lret;
	 BTNode* rret = TreeFind(root->right,x);
	if (rret)
		return rret;
	//左右都没找到
	return NULL;
}

9、销毁

void BinaryTreeDestoty(BTNode** proot)//后序销毁
{
	//
	if (*proot == NULL)
		return;
	BinaryTreeDestoty(&(*proot)->left);
	BinaryTreeDestoty(&(*proot)->right);
	free(*proot);
	*proot = NULL;

}

二叉树的前、中、后序就是深度优先遍历

广度优先遍历

思路：
1、先把根入队列
2、出队头的数据，把它的下一层入队

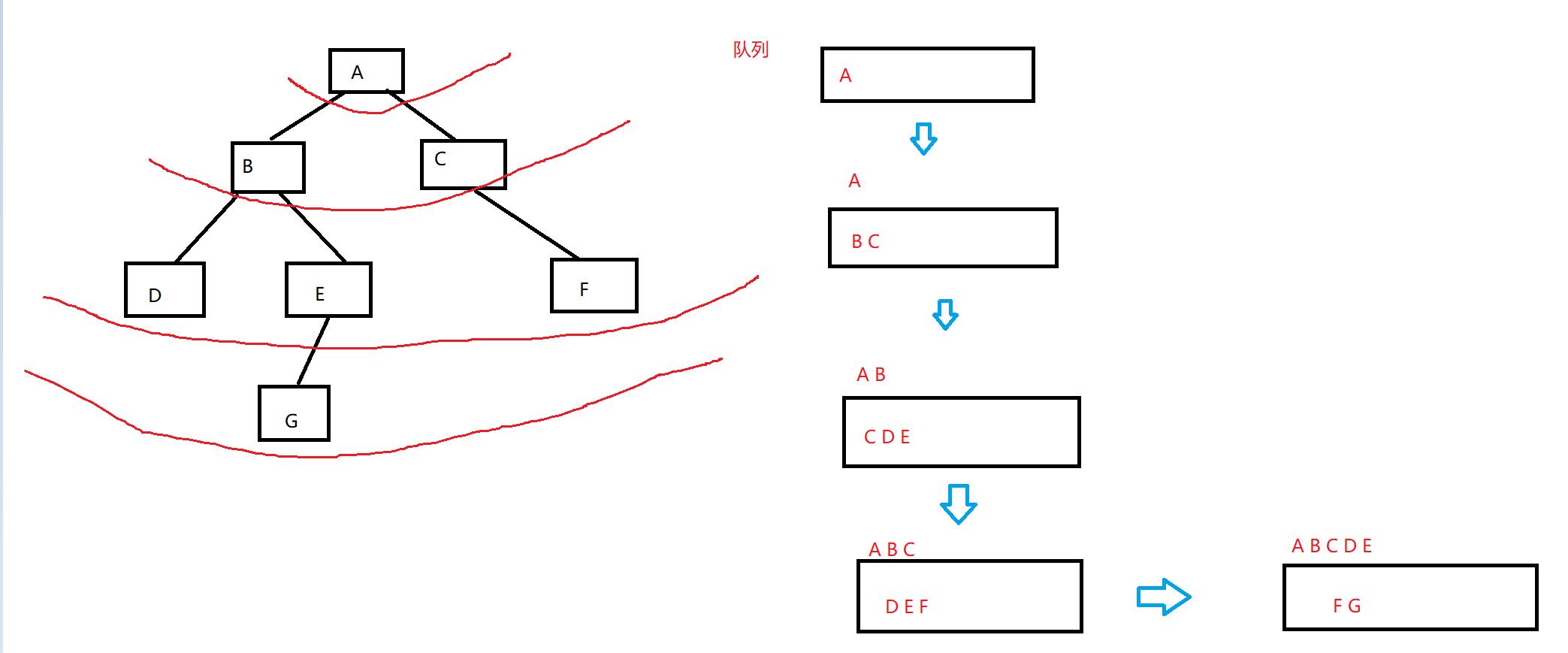
特点：借助队列先进先出的性质，
上一层出队，下一层入队

void TreeLevelOrder(BTNode* root)
{
	Queue q;
	QueueInit(&q);
	if (root == NULL)
	{
		QueuePush(&q, root->data);
	}
	while (!QueueEmpty(&q))
	{
		BTNode* front = QueueFront(&q);
		QueuePop(&q);
		printf("%c", front->data);
		if (front->left)
			QueuePush(&q, front->left->data);
		if (front->right)
			QueuePush(&q, front->right->data);
	}

	QueueDestroy(&q);
}

10、判断是否为完全二叉树

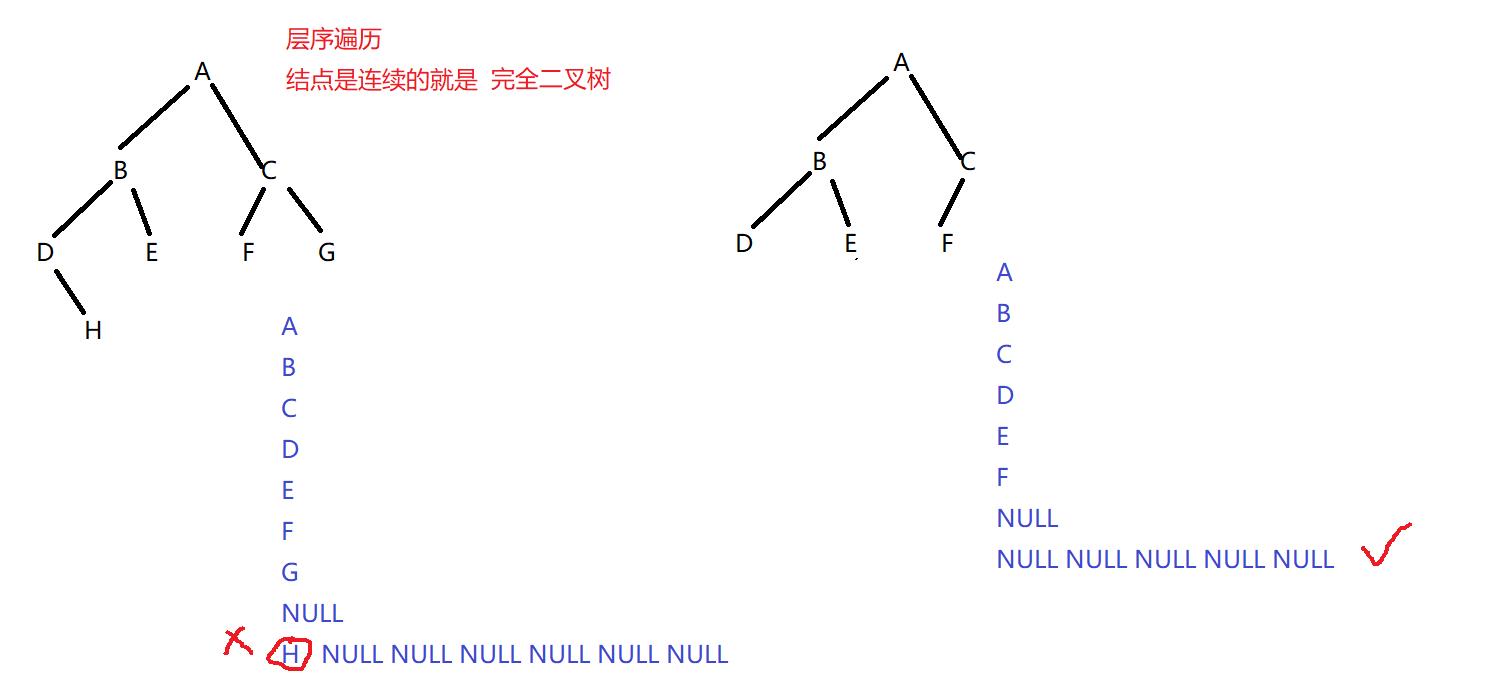
bool BinaryTreeCompelet(BTNode* root)
{
	Queue q;
	QueueInit(&q);
	if (root)
		QueuePush(&q, root->data);
	while (!QueueEmpty(&q))
	{
		BTNode* front = QueueFront(&q);
		QueuePop(&q);
		if (front == NULL)
			break;
		QueuePush(&q, front->left->data);
		QueuePush(&q, front->right->data);
	}
	while (!QueueEmpty(&q))
	{
		BTNode* front = QueueFront(&q);
		QueuePop(&q);
		if (front)
			return false;
	}
	QueueDestroy(&q);
	return true;
}

注：队列的函数在另一篇博客：队列