路径规划基于粒子群算法实现避障规划matlab源码

Posted 2021-06-20 MatlabQQ1575304183

1.理论基础

粒子群算法（particle swarm optimization，PSO）是计算智能领域中的一种生物启发式方法，属于群体智能优化算法的一种，常见的群体智能优化算法主要有如下几类：
　　（1）蚁群算法（Ant Colony Optimization，简称ACO）[1992年提出]；
　　（2）粒子群优化算法（Particle Swarm Optimization，简称PSO）[1995年提出]（简单易于实现，也是目前应用最为广泛的群体智能优化算法）；
　　（3）菌群优化算法（Bacterial Foraging Optimization，简称BFO）[2002年提出]；
　　（4）蛙跳算法（Shuffled Frog Leading Algorithm，简称SFLA）[2003年提出]；
　　（5）人工蜂群算法（Artificial Bee Colony Algorithm，简称ABC）[2005年提出]；
　　除了上述几种常见的群体智能算法以外，还有一些并不是广泛应用的群体智能算法，比如萤火虫算法、布谷鸟算法、蝙蝠算法以及磷虾群算法等等。

而其中的粒子群优化算法（PSO）源于对鸟类捕食行为的研究，鸟类捕食时，找到食物最简单有限的策略就是搜寻当前距离食物最近的鸟的周围。

举个通俗的例子：

一群鸟在寻找食物，在这个区域内有一个食物，所有的鸟都不知道食物在哪里，但食物发出了香味，鸟通过香味的浓烈能判断出自己的当前位置距离食物有多远，同时鸟群之间是可以交流并告知离食物最近的鸟的位置的。试想一下这个时候会发生什么？

鸟甲：哈哈哈，原来我离食物最近！

鸟乙、丙、丁…:我得赶紧往鸟甲那里过去看看！

同时各自鸟在位置不停变化的时候，离食物的距离也不断的变化，所以一定有过离食物最近的位置，这是他们的一个参考。

鸟某某：我刚才的位置好像离食物很近了，我得往那里再靠近点！

通过这样一个过程，不断的变化，最终鸟群会向食物方向聚集，达到目标。在这个变化的过程中，影响鸟的运动状态变化的有两个因素：

• 离食物最近的鸟的位置
• 自己之前达到过的离食物最近的位置

而鸟的每次的位置变化，除了考虑以上的两个因素还有一个因素就是惯性。而对位置的变化，通过变化量（速度）来表示。

通过以上的例子，我们可以把鸟抽象为没有质量和体积的微粒(点)，并延伸到N维空间，粒子I 在N维空间的位置表示为矢量Xi＝(x1，x2，…，xN)，飞行速度表示为矢量Vi＝(v1，v2，…，vN)．每个粒子都有一个由目标函数决定的适应值(fitness value)，并且知道自己到目前为止发现的最好位置(pbest)和现在的位置Xi．这个可以看作是粒子自己的飞行经验．除此之外，每个粒子还知道到目前为止整个群体中所有粒子发现的最好位置(gbest)(gbest是pbest中的最好值)．这个可以看作是粒子同伴的经验．粒子就是通过自己的经验和同伴中最好的经验来决定下一步的运动。归结为下面的两个公式：

                                                    (公式-1）

                                                                                              （公式-2）

其中，为惯性权重因子，（什么是权重因子，这个后面会讲到，此处大概知道有这么一个参数即可）；d=1,2，…，D；i=1,2，…，n；k为当前迭代次数；Vid为粒子的速度；c1和c2是非负的常数，称为加速因子；r1和r2是分布于[0,1]区间的随机数。为了防止粒子的满目搜索，一般建议限制位置和速度在一定的区间。

2.粒子群寻优算法的案例与实现

假设有如下非线性函数，需要在一定范围内找出最大值和最大值的位置，本文用Python实现。

                                                    （公式-3）

我们先通过python把上面函数使用matplotlib把它画处理，让我们有个直观的感受。

1. # -*- coding: utf-8 -*-

2. from mpl_toolkits.mplot3d import Axes3D

3. import matplotlib.pyplot as plt

4. import numpy as np

5.  

6. fig = plt.figure()

7. ax = Axes3D(fig)

8. X = np.arange(-2, 2, 0.05)

9. Y = np.arange(-2, 2, 0.05)

10. X, Y = np.meshgrid(X, Y)

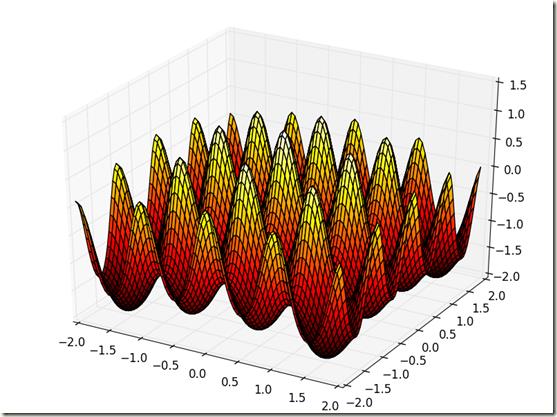
11. Z = np.sin(np.sqrt(X**2+Y**2))/np.sqrt(X**2+Y**2)+np.exp((np.cos(2*np.pi*X)+np.cos(2*np.pi*Y))/2)-2.71289

12.  

13. ax.plot_surface(X, Y, Z, rstride=1, cstride=1, cmap='hot')

14. plt.show()

此处使用mpl_toolkits.mplot3d画3D图，在代码中，分别使用numpy中的arange创建等差长度为0.05的数据点向量，区间为[-2,2]之间，然后使用meshgrid将向量转换给对应的矩阵，这样的话，后面的函数式中就可以使用np中的三角函数和数学函数了，如果不这样的话，还得一个一个点的根据公式去做循环，拼接Z的向量点。

运行出来的图如下：

从函数图形中可以看出，这个函数有很多的局部极大值，而真正的极限位置就是在（0,0），极大值为1.005。下面就通过粒子群算法来找寻这个极大值和极大值的位置。根据粒子群算法函数求极值的算法流程如下图所示：

在pycham作为python的IDE中，建立一个名为PSO.py的文件，文件中编写一个名PSO的类。

2.1 参数的设定

设置惯性参数为常数1，也就是公式-1中的为常数1；设置加速度因子为非负的两个常数，公式-1的中的c1和c2；设置迭代次数为300；设置粒子群的规模为20；为了防止粒子的盲目搜索，将位置和速度限制在区间[-2,2]、[-0.5,0.5]；

具体代码如下：

1. def __init__(self):

2. self.iter=300 #迭代次数

3. self.w=1 #惯性权重

4. self.lr = (0.49445, 1.49445) #粒子群个体和社会的学习因子，即加速常数

5. self.sizepop=20 #种群规模

6. self.rangepop=(-2,2) #粒子的位置的范围限制,x、y方向的限制相同

7. self.rangespeed=(-0.5,0.5) #速度限制

8. self.px=[] #当前全局最优解

9. self.py=[]

 

2.2 种群初始化

随机初始化粒子位置和粒子的速度，并根据适应度函数计算粒子适应度值，我们的适应度函数就是公式-3这个函数。

首先定义一个适应度函数

1. def func(self,x):

2. # x输入粒子位置

3. # y 粒子适应度值

4. if (x[0]==0)&(x[1]==0):

5. y = np.exp((np.cos(2*np.pi*x[0])+np.cos(2*np.pi*x[1]))/2)-2.71289

6. else:

7. y = np.sin(np.sqrt(x[0]**2+x[1]**2))/np.sqrt(x[0]**2+x[1]**2)+np.exp((np.cos(2*np.pi*x[0])+np.cos(2*np.pi*x[1]))/2)-2.71289

8. return y

然后初始化粒子和计算适应度值

1. def initpopvfit(self,sizepop):

2. pop = np.zeros((sizepop,2))

3. v = np.zeros((sizepop,2))

4. fitness = np.zeros(sizepop)

5.  

6. for i in range(sizepop):

7. pop[i] = [(np.random.rand()-0.5)*self.rangepop[0]*2,(np.random.rand()-0.5)*self.rangepop[1]*2]

8. v[i] = [(np.random.rand()-0.5)*self.rangepop[0]*2,(np.random.rand()-0.5)*self.rangepop[1]*2]

9. fitness[i] = self.func(pop[i])

10. return pop,v,fitness

2.3 寻找初始化后的极值

1. def getinitbest(self,fitness,pop):

2. # 群体最优的粒子位置及其适应度值

3. gbestpop,gbestfitness = pop[fitness.argmax()].copy(),fitness.max()

4. #个体最优的粒子位置及其适应度值,使用copy()使得对pop的改变不影响pbestpop，pbestfitness类

5. 似

6. pbestpop,pbestfitness = pop.copy(),fitness.copy()

7.  

8. return gbestpop,gbestfitness,pbestpop,pbestfitness

此处需要分别找到群体极值和个体粒子的极值。

2.4 迭代寻优

通过循环迭代，不断的更新粒子的位置和速度，根据新粒子的适应度值更新个体和群体的极值。这部分的代码如下：

1. def run(self):

2. """

3. 通过循环迭代，不断的更新粒子的位置和速度，根据新粒子的适应度值更新个体和群体的极值

4. :return:

5. """

6. pop, v, fitness = self.initpopvfit(self.sizepop)

7. gbestpop, gbestfitness, pbestpop, pbestfitness = self.getinitbest(fitness, pop)

8.  

9. result = np.zeros(self.iter)

10. for i in range(self.iter):

11. # 速度更新

12. for j in range(self.sizepop):

13. v[j] = self.w*v[j] +self.lr[0] * np.random.rand() * (pbestpop[j] - pop[j]) + self.lr[1] * np.random.rand() * (

14. gbestpop - pop[j])

15. v[v < self.rangespeed[0]] = self.rangespeed[0]

16. v[v > self.rangespeed[1]] = self.rangespeed[1]

17.  

18. # 粒子位置更新

19. for j in range(self.sizepop):

20. pop[j] +=v[j]

21. pop[pop < self.rangepop[0]] = self.rangepop[0]

22. pop[pop > self.rangepop[1]] = self.rangepop[1]

23.  

24. # 适应度更新

25. for j in range(self.sizepop):

26. fitness[j] = self.func(pop[j])

27.  

28. for j in range(self.sizepop):

29. if fitness[j] > pbestfitness[j]:

30. pbestfitness[j] = fitness[j]

31. pbestpop[j] = pop[j].copy()

32.  

33. if pbestfitness.max() > gbestfitness:

34. gbestfitness = pbestfitness.max()

35. gbestpop = pop[pbestfitness.argmax()].copy()

36.  

37. result[i] = gbestfitness

38. self.px.append(gbestpop[0])

39. self.py.append(gbestpop[1])

40. return result,self.px,self.py

2.5 绘图

   

1. def drawPaht(self,X, Y, Z, px, py, pz):

2. """

3. 绘图

4. """

5. fig = plt.figure()

6. ax = Axes3D(fig)

7. plt.title("PSO")

8. ax.plot_surface(X, Y, Z, rstride=1, cstride=1, color='b', )

9. ax.set_xlabel('x label', color='r')

10. ax.set_ylabel('y label', color='g')

11. ax.set_zlabel('z label', color='b')

12. ax.plot(px, py, pz, 'r.') # 绘点x

13. plt.show()

2.6 结果分析

通过在主函数文件中，实例化PSO类，调用run这个函数，运行上面的代码

1. def f(X,Y):

2. return np.sin(np.sqrt(X ** 2 + Y ** 2)) / np.sqrt(X ** 2 + Y ** 2) + np.exp(

3. (np.cos(2 * np.pi * X) + np.cos(2 * np.pi * Y)) / 2) - 2.71289

4. pso = PSO()

5. result,px,py = pso.run()

6. print(max(result),result.argmax())

7.  

8. plt.plot(result)

9.  

10. X = np.arange(-2, 2, 0.05)

11. Y = np.arange(-2, 2, 0.05)

12. X, Y = np.meshgrid(X, Y)

13. Z= f(X,Y)

14. pso.drawPaht(X,Y,Z,px,py,f(np.array(px),np.array(py)))

15. plt.show()

当迭代了300次之后，画出每代最优个体适应度值的曲线，结果如下：

  

 

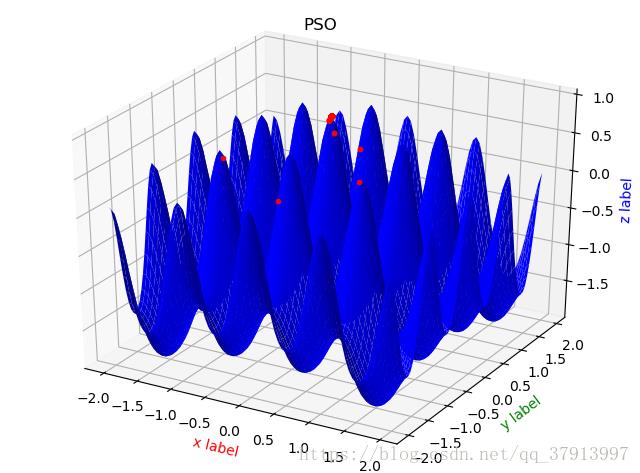
最终得到的最优个体适应度值为：1.00538866933，对应的粒子位置为：[  2.37513360e-05   3.41265823e-04]，通过比较，PSO算法能得到最优值，接近函数实际的最优值1.005。

通过以上，证明PSO算法具有较强的函数极值寻优能力。后面附上全部代码。

clc;
clear;
close all;

%% Problem Definition

model=CreateModel2();

model.n=5;  % number of Handle Points

CostFunction=@(x) MyCost(x,model);    % Cost Function

nVar=model.n;       % Number of Decision Variables

VarSize=[1 nVar];   % Size of Decision Variables Matrix

VarMin.x=model.xmin;           % Lower limit of Variables
VarMax.x=model.xmax;           % Upper limit of Variables
VarMin.y=model.ymin;           % Lower limit of Variables
VarMax.y=model.ymax;           % Upper limit of Variables


%% PSO Parameters

MaxIt=50;          % Maximum Number of Iterations

nPop=15;           % Population Size (Swarm Size)

w=1;                % Inertia Weight
wdamp=0.98;         % Inertia Weight Damping Ratio
c1=1.5;             % Personal Learning Coefficient
c2=1.5;             % Global Learning Coefficient

alpha=0.1;
VelMax.x=alpha*(VarMax.x-VarMin.x);    % Maximum Velocity
VelMin.x=-VelMax.x;                    % Minimum Velocity
VelMax.y=alpha*(VarMax.y-VarMin.y);    % Maximum Velocity
VelMin.y=-VelMax.y;                    % Minimum Velocity

%% Initialization


    
end

%% Results

figure;
plot(BestCost,'LineWidth',2);
xlabel('Iteration');
ylabel('Best Cost');
grid on;

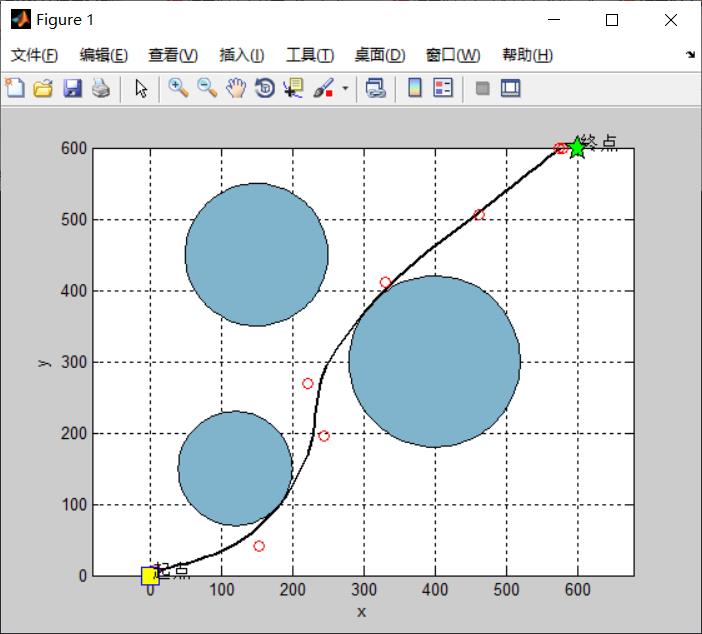
完整代码或者仿真咨询添加QQ1575304183