霍夫曼树和霍夫曼编码以及霍夫曼编码的应用
Posted 活跃的咸鱼
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了霍夫曼树和霍夫曼编码以及霍夫曼编码的应用相关的知识,希望对你有一定的参考价值。
文章目录
霍夫曼树介绍
1.1霍夫曼树的定义
给定N个权值作为N个叶子结点,构造一棵二叉树,若该树的带权路径长度达到最小,称这样的二叉树为最优二叉树,也称为哈夫曼树(Huffman Tree)。哈夫曼树是带权路径长度最短的树,权值较大的结点离根较近。
1.2霍夫曼树的几个概念
路径和路径长度:在一棵树中,从一个结点往下可以达到的孩子或孙子结点之间的通路,称为路径。通路中分支的数目称为路径长度。若规定根结点的层数为1,则从根结点到第L层结点的路径长度为L-1。
结点的权及带权路径长度:若将树中结点赋给一个有着某种含义的数值,则这个数值称为该结点的权。结点的带权路径长度为:从根结点到该结点之间的路径长度与该结点的权的乘积
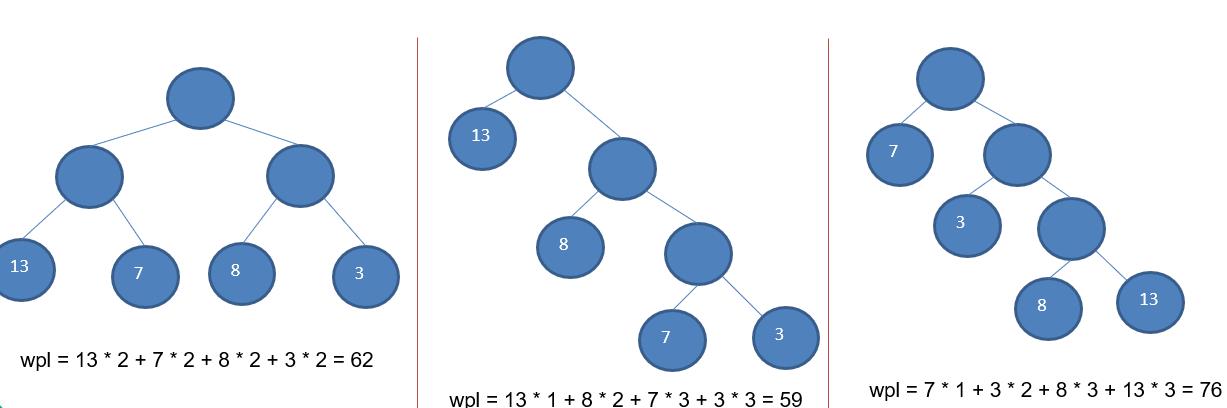
树的带权路径长度:树的带权路径长度规定为所有叶子结点的带权路径长度之和,记为WPL(weighted path length) ,权值越大的结点离根结点越近的二叉树才是最优二叉树。WPL最小的就是赫夫曼树,如下图所示:第二个便是霍夫曼树
1.3构建霍夫曼树的过程
构成霍夫曼树的步骤:
- 从小到大进行排序, 将每一个数据,每个数据都是一个节点 , 每个节点可以看成是一颗最简单的二叉树。
- 取出根节点权值最小的两颗二叉树 。
- 组成一颗新的二叉树, 该新的二叉树的根节点的权值是前面两颗二叉树根节点权值的和。
- 再将这颗新的二叉树,以根节点的权值大小 再次排序, 不断重复 1-2-3-4 的步骤,直到数列中,所有的数据都被处理,就得到一颗霍夫曼树。
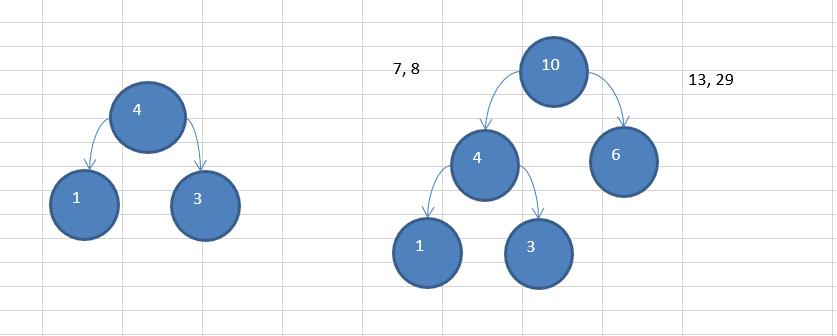
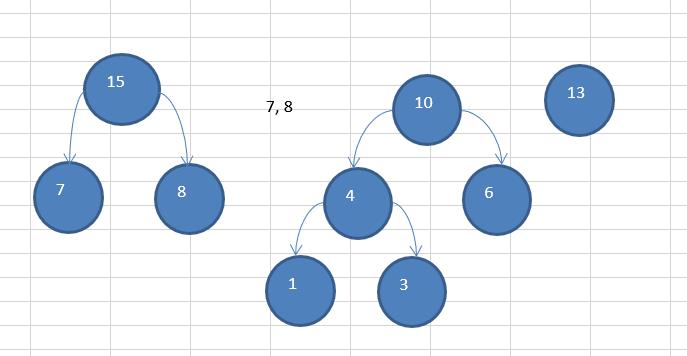
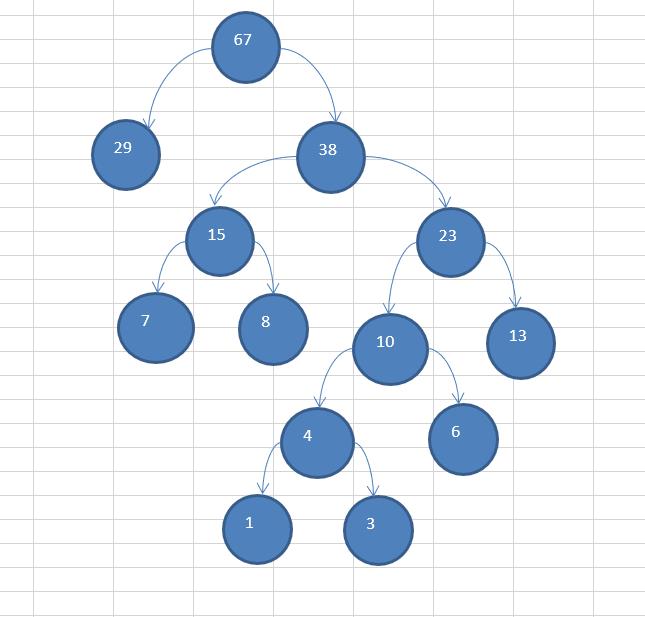
以该数列为例来构建霍夫曼树:{13, 7, 8, 3, 29, 6, 1}
排序 1, 3, 6, 7, 8, 13, 29 按照如上步骤进行构建如下图;
1.4代码实现霍夫曼树
构成霍夫曼树的步骤:
- 从小到大进行排序, 将每一个数据,每个数据都是一个节点 , 每个节点可以看成是一颗最简单的二叉树。
- 取出根节点权值最小的两颗二叉树 。
- 组成一颗新的二叉树, 该新的二叉树的根节点的权值是前面两颗二叉树根节点权值的和。
- 再将这颗新的二叉树,以根节点的权值大小 再次排序, 不断重复 1-2-3-4 的步骤,直到数列中,所有的数据都被处理,就得到一颗霍夫曼树。
public class HuffmanTree {
public static void main(String[] args) {
int arr[] = { 13, 7, 8, 3, 29, 6, 1 };
Node root = createHuffmanTree(arr);
System.out.println("构造后的霍夫曼树的根结点"+"\\n"+root);
System.out.println("前序遍历霍夫曼树");
preOrder(root);
}
//前序遍历
public static void preOrder(Node root) {
if(root!=null){
System.out.println(root);
preOrder(root.leftNode);
preOrder(root.rightNode);
}
}
public static Node createHuffmanTree(int[] arr) {
// 1. 遍历 arr 数组
// 2. 将arr的每个元素构成成一个Node
// 3. 将Node 放入到ArrayList中
ArrayList<Node> nodes = new ArrayList<>();
for (int i = 0; i < arr.length; i++) {
nodes.add(new Node(arr[i]));
}
while (nodes.size()>1) {
//排序 从小到大
Collections.sort(nodes);
//取出根节点权值最小的两颗二叉树
Node leftNode = nodes.get(0);
Node rightNode = nodes.get(1);
//(3)构建一颗新的二叉树
Node parent = new Node(leftNode.value + rightNode.value);
parent.leftNode = leftNode;
parent.rightNode = rightNode;
//(4)从ArrayList删除处理过的二叉树
nodes.remove(leftNode);
nodes.remove(rightNode);
//(5)将parent加入到nodes
nodes.add(parent);
}
//返回哈夫曼树的root结点
return nodes.get(0);
}
}
class Node implements Comparable<Node>{
int value;
Node leftNode;
Node rightNode;
public Node(int value) {
this.value = value;
}
@Override
public String toString() {
return "Node{" +
"value=" + value +
'}';
}
@Override
public int compareTo(Node o) {
return this.value-o.value;
}
}
构造后的霍夫曼树的根结点
Node{value=67}
前序遍历霍夫曼树
Node{value=67}
Node{value=29}
Node{value=38}
Node{value=15}
Node{value=7}
Node{value=8}
Node{value=23}
Node{value=10}
Node{value=4}
Node{value=1}
Node{value=3}
Node{value=6}
Node{value=13}
霍夫曼编码介绍
什么是霍夫曼编码
- 霍夫曼编码也翻译为 哈夫曼编码(Huffman Coding),又称霍夫曼编码,是一种编码方式, 属于一种程序算法
- 霍夫曼编码是赫哈夫曼树在电讯通信中的经典的应用之一。
- 霍夫曼编码广泛地用于数据文件压缩。其压缩率通常在20%~90%之间
- 霍夫曼码是可变字长编码(VLC)的一种。Huffman于1952年提出一种编码方法,称之为最佳编码
- 规定哈夫曼树中的左分支为0,右分支为1,则从根节点到每个 叶节点所经过的分支对应的0和1组成的序列便为该节点对应字符的 编码。这样的编码称为哈夫曼编码。哈夫曼编码属0、1二 进制编码
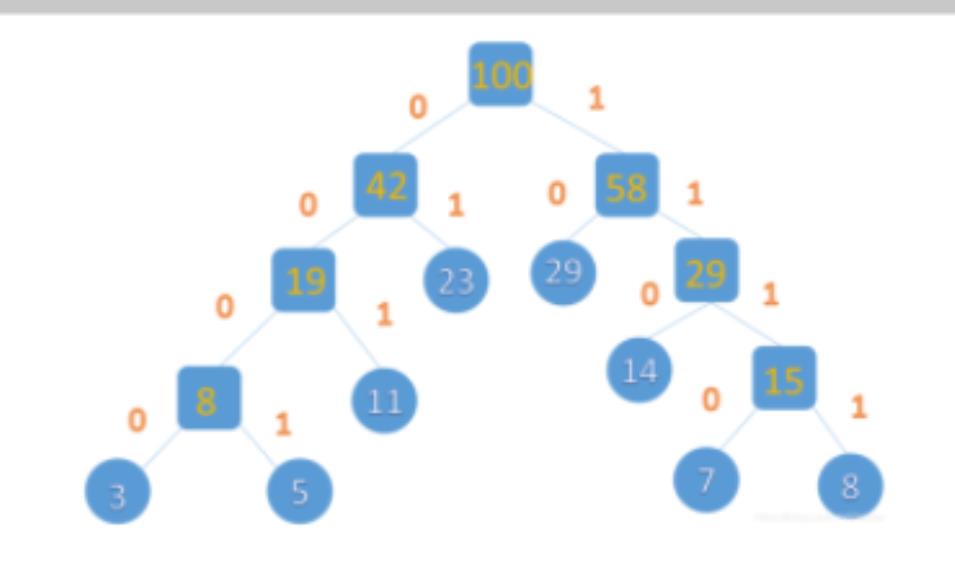
如图:5的二进制编码就是(0,0,0,1),以此类推其他的结点:
3:(0000) 5:(0001) 11:(001) 23:(01)
8:(1111) 7:(1110) 14:(110) 29:(10)
通信领域的应用
在电文传输中,需要将电文中出现的每个字符进行二进制编码。在设计编码时需要遵守两个原则:
(1)发送方传输的二进制编码,到接收方解码后必须具有唯一性,即解码结果与发送方发送的电文完全一样;
(2)发送的二进制编码尽可能地短。下面我们介绍两种编码的方式。
-
等长编码
这种编码方式的特点是每个字符的编码长度相同(编码长度就是每个编码所含的二进制位数)。假设字符集只含有4个字符A,B,C,D,用二进制两位表示的编码分别为00,01,10,11。若现在有一段电文为:ABACCDA,则应发送二进制序列:00010010101100,总长度为14位。当接收方接收到这段电文后,将按两位一段进行译码。这种编码的特点是译码简单且具有唯一性,但编码长度并不是最短的。 -
不等长编码
在传送电文时,为了使其二进制位数尽可能地少,可以将每个字符的编码设计为不等长的,使用频度较高的字符分配一个相对比较短的编码,使用频度较低的字符分配一个比较长的编码。例如,可以为A,B,C,D四个字符分别分配0,00,1,01,并可将上述电文用二进制序列:000011010发送,其长度只有9个二进制位,但随之带来了一个问题,接收方接到这段电文后无法进行译码,因为无法断定前面4个0是4个A,1个B、2个A,还是2个B,即译码不唯一,因此这种编码方法不可使用。 -
压缩
采用哈夫曼静态编码的方式,通过对数据进行两遍扫描,第一次统计出现的字符频次,进而构造霍夫曼树,第二遍扫描数据根据得到的霍夫曼树对数据进行编码。
注意:
这个霍夫曼树根据排序方法不同,也可能不太一样,这样对应的霍夫曼编码也不完全一样,但是wpl 是一样的,都是最小的。
字符串压缩
1.构造霍夫曼树
例如有一个字符串String s=“i like java do you like too?”;共28个字符包括空格
我们用霍夫曼编码来对其压缩,其压缩过程如下:
- 先找出各个字符出现的次数
i:3,l:2,k:2,e:2,j:1,v:1,a:2,y:1,o:4,u:1,t:1,空格:6,?:1。
可以用一个map[key,value]将上面的字符以及出现的次数保存。 - 按照上面字符出现的次数构建一颗赫夫曼树, 次数作为权值
结点
class Node implements Comparable<Node> {
Byte data; // 存放数据(字符)本身,比如'a' => 97 ' ' => 32
int weight; //权值, 表示字符出现的次数
Node left;//
Node right;
public Node(Byte data, int weight) {
this.data = data;
this.weight = weight;
}
@Override
public int compareTo(Node o) {
// 从小到大排序
return this.weight - o.weight;
}
public String toString() {
return "Node [data = " + data + " weight=" + weight + "]";
}
//前序遍历
public void preOrder() {
System.out.println(this);
if(this.left != null) {
this.left.preOrder();
}
if(this.right != null) {
this.right.preOrder();
}
}
}
/**
*
* @param bytes 接收字节数组
* @return 返回的就是 List
*/
private static List<Node> getNodes(byte[] bytes) {
//1创建一个ArrayList
ArrayList<Node> nodes = new ArrayList<Node>();
//遍历 bytes , 统计 每一个byte出现的次数->map[key,value]
Map<Byte, Integer> counts = new HashMap<>();
for (byte b : bytes) {
Integer count = counts.get(b);
if (count == null) { // Map还没有这个字符数据,第一次
counts.put(b, 1);
} else {
counts.put(b, count + 1);
}
}
//把每一个键值对转成一个Node 对象,并加入到nodes集合
//遍历map
for(Map.Entry<Byte, Integer> entry: counts.entrySet()) {
nodes.add(new Node(entry.getKey(), entry.getValue()));
}
return nodes;
}
//可以通过List 创建对应的赫夫曼树
private static Node createHuffmanTree(List<Node> nodes) {
while(nodes.size() > 1) {
//排序, 从小到大
Collections.sort(nodes);
//取出第一颗最小的二叉树
Node leftNode = nodes.get(0);
//取出第二颗最小的二叉树
Node rightNode = nodes.get(1);
//创建一颗新的二叉树,它的根节点 没有data, 只有权值
Node parent = new Node(null, leftNode.weight + rightNode.weight);
parent.left = leftNode;
parent.right = rightNode;
//将已经处理的两颗二叉树从nodes删除
nodes.remove(leftNode);
nodes.remove(rightNode);
//将新的二叉树,加入到nodes
nodes.add(parent);
}
//nodes 最后的结点,就是赫夫曼树的根结点
return nodes.get(0);
}
测试:
public static void main(String[] args) {
String s="i like java do you like java too?";
List<Node> nodes = getNodes(s.getBytes());
System.out.println(nodes);
Node tree = createHuffmanTree(nodes);
System.out.println(tree);
}
[Node [data = 32 weight=7], Node [data = 97 weight=4], Node [data = 100 weight=1],
Node [data = 101 weight=2], Node [data = 105 weight=3], Node [data = 106 weight=2], Node [data = 107 weight=2],
Node [data = 108 weight=2], Node [data = 111 weight=4], Node [data = 116 weight=1], Node
[data = 117 weight=1], Node [data = 118 weight=2], Node [data = 121 weight=1], Node [data = 63 weight=1]]
Node [data = null weight=33]
2.生成赫夫曼树对应的赫夫曼编码表
生成的赫夫曼编码表形如{32=01, 97=100, 100=11000, 117=11001, 101=1110, 118=11011, 105=101, 121=11010, 106=0010, 107=1111, 108=000, 111=0011}
将赫夫曼编码表存放在 Map<Byte,String> 中
static Map<Byte, String> huffmanCodes = new HashMap<Byte,String>();
//在生成赫夫曼编码表示,需要去拼接路径, 定义一个StringBuilder 存储某个叶子结点的路径
static StringBuilder stringBuilder = new StringBuilder();
/**
* 功能:将传入的node结点的所有叶子结点的赫夫曼编码得到,并放入到huffmanCodes集合
* @param node 传入结点
* @param code 路径: 左子结点是 0, 右子结点 1
* @param stringBuilder 用于拼接路径
*/
private static void getCodes(Node node, String code, StringBuilder stringBuilder) {
StringBuilder stringBuilder2= new StringBuilder(stringBuilder);
//将code 加入到 stringBuilder2
stringBuilder2.append(code);
if(node != null) { //如果node == null不处理
//判断当前node 是叶子结点还是非叶子结点
if(node.data == null) { //非叶子结点
//递归处理
//向左递归
getCodes(node.left, "0", stringBuilder2);
//向右递归
getCodes(node.right, "1", stringBuilder2);
} else { //说明是一个叶子结点
//就表示找到某个叶子结点的最后
huffmanCodes.put(node.data, stringBuilder2.toString());
}
}
}
//为了调用方便,我们重载 getCodes
private static Map<Byte, String> getCodes(Node root) {
if(root == null) {
return null;
}
//处理root的左子树
getCodes(root.left, "0", stringBuilder);
//处理root的右子树
getCodes(root.right, "1", stringBuilder);
return huffmanCodes;
}
测试:
public static void main(String[] args) {
String s="i like java do you like java too?";
List<Node> nodes = getNodes(s.getBytes());
Node root= createHuffmanTree(nodes);
System.out.println("得到霍夫曼编码表");
Map<Byte, String> map = getCodes(root);
System.out.println(map);
}
得到霍夫曼编码表
{32=00, 97=010, 100=11000, 101=11111, 105=1110, 106=1000, 107=1001, 108=1010, 111=011, 116=11001, 117=11010, 118=1011, 121=11011, 63=11110}
3.通过生成的赫夫曼编码表,返回一个赫夫曼编码 压缩后的byte[]
/**
* @param bytes 这时原始的字符串对应的 byte[]
* @param huffmanCodes 生成的赫夫曼编码map
* @return 返回赫夫曼编码处理后的 byte[]
* 举例: String content = "i like java do you like java too?"; =》 byte[] contentBytes = content.getBytes();
* 返回的是 字符串 "1010100010111111110010001011111111001000101111111100100101001101110001110000011011101000111100101000101111111100110001001010011011100"
* => 对应的 byte[] huffmanCodeBytes ,即 8位对应一个 byte,放入到 huffmanCodeBytes
* huffmanCodeBytes[0] = 10101000(补码) => byte [推导 10101000=> 10101000 - 1 => 10100111(反码)=> 11011000= -88 ]
* huffmanCodeBytes[1] = -88
*/
private static byte[] zip(byte[] bytes, Map<Byte, String> huffmanCodes) {
//1.利用 huffmanCodes 将 bytes 转成 赫夫曼编码对应的字符串
StringBuilder stringBuilder = new StringBuilder();
//遍历bytes 数组
for(byte b: bytes) {
stringBuilder.append(huffmanCodes.get(b));
}
//将 "1010100010111111110..." 转成 byte[]
//统计返回 byte[] huffmanCodeBytes 长度
//一句话 int len = (stringBuilder.length() + 7) / 8;
int len;
if(stringBuilder.length() % 8 == 0) {
len = stringBuilder.length() / 8;
} else {
len = stringBuilder.length() / 8 + 1;
}
//创建 存储压缩后的 byte数组
byte[] huffmanCodeBytes = new byte[len];
int index = 0;//记录是第几个byte
for (int i = 0; i < stringBuilder.length(); i += 8) { //因为是每8位对应一个byte,所以步长 +8
String strByte;
if(i+8 > stringBuilder.length()) {//不够8位
strByte = stringBuilder.substring(i);
}else{
strByte = stri以上是关于霍夫曼树和霍夫曼编码以及霍夫曼编码的应用的主要内容,如果未能解决你的问题,请参考以下文章