[CF1503E]2-Coloring

Posted 2021-06-20 Tan_tan_tann

2-Coloring

题解

首先，我们可以发现黄色从列1到列n与蓝色从行1到行n的路径两者中最多有一个存在。
如果两者都存在的话，必定会有一个交点。
所以，我们得到的一定是下面的两种情况之一：

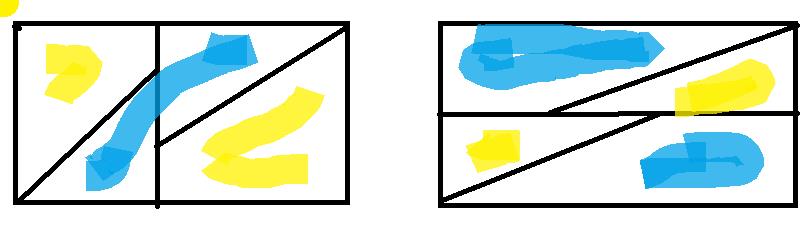
仔细看这两种情况是一样的，不过是将$m,n$换一下，我们先来考虑第一种情况：

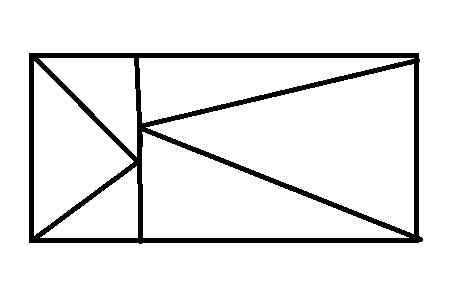
很明显，两边都是三角形状的结构，由于每列都要有，所以两个三角形的定点应该在一条线的两侧。
由于不能连通，两者与线相接触的地方是不同的。
我们可以先枚举相交的线的位置$l$，与两个交点的位置$u,d(u⩽d)$，由于左右侧可以交换来表示不同情况，不妨先假设左端在上，右端在下。
左半边的方案数为$\left(\genfrac{}{}{0ex}{}{l+u-1}{u-1}\right)\left(\genfrac{}{}{0ex}{}{n-u+l-1}{n-u}\right)$
我们可以将其转化为路径来理解：
由于下半部分不能与右端相碰，所以要先往左走，然后从$(u,l-1)$走到$(n,0)$
而上半部分需保证与边界线接触的至少有一个格子，所以先往上走，然后从$(u-1,l)$走到$(0,0)$
右半边同理，方案数为$\left(\genfrac{}{}{0ex}{}{m-l-1+d}{d}\right)\left(\genfrac{}{}{0ex}{}{n-d-1+m-l}{n-d-1}\right)$
由于还有左在下右在上的情况，我们还要将答案乘上2。
这样的答案为
$$Ans=2\sum _{i=1}^{m-1}\sum _{j=1}^{n-1}\sum _{k=j+1}^n\left(\genfrac{}{}{0ex}{}{i+j-1}{j-1}\right)\left(\genfrac{}{}{0ex}{}{n-j+i-1}{n-j}\right)\left(\genfrac{}{}{0ex}{}{m-i-1+k}{k}\right)\left(\genfrac{}{}{0ex}{}{m-i+n-k-1}{n-k-1}\right)$$
再将$n$与$m$交换一下，求另一种情况。

但我们真的有必要求另一种情况吗？
如果根据上面的式子算的话，是根本不需要$\times 2$的。
另外一种情况已经被包含在了我们这里面了。
实际的图长这样

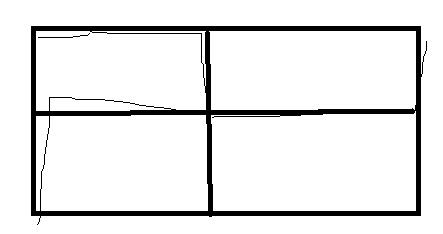
如果我们将一极枚举到$n$的话相当于那一半我们根本没有黄格子。
仔细观察一下，这些部分刚好可以被转化成另外一半。
所以所，我们直接将这个作为答案即可。
这刚好也包含了没有路径的情况，可以打出来跑跑试试。

时间复杂度$O\left(n^2\right)$。

源码

#include<bits/stdc++.h>
using namespace std;
#define MAXN 200005
#define lowbit(x) (x&-x)
#define reg register
#define mp make_pair
#define fir first
#define sec second
typedef long long LL;
typedef unsigned long long uLL;
typedef unsigned int uint;
const int INF=0x7f7f7f7f;
const int jzm=233;
const int mo=998244353;
const double Pi=acos(-1.0);
typedef pair<int,int> pii;
const double PI=acos(-1.0);
template<typename _T>
_T Fabs(_T x){return x<0?-x:x;}
template<typename _T>
void read(_T &x){
	_T f=1;x=0;char s=getchar();
	while(s>'9'||s<'0'){if(s=='-')f=-1;s=getchar();}
	while('0'<=s&&s<='9'){x=(x<<3)+(x<<1)+(s^48);s=getchar();}
	x*=f;
}
int n,m,ans,fac[MAXN],inv[MAXN],f[MAXN];
int add(int x,int y){return x+y<mo?x+y:x+y-mo;}
void init(){
	fac[0]=fac[1]=inv[0]=inv[1]=f[1]=1;
	for(int i=2;i<=n+m;i++){
		fac[i]=1ll*fac[i-1]*i%mo;
		f[i]=1ll*(mo-mo/i)*f[mo%i]%mo;
		inv[i]=1ll*inv[i-1]*f[i]%mo;
	}
}
int C(int x,int y){if(x<0||y<0||x<y)return 0;return 1ll*fac[x]*inv[y]%mo*inv[x-y]%mo;}
int sakura(){
	int res=0;
	for(int i=1;i<m;i++)
		for(int j=n-1,sum=0;j>0;j--){
			sum=add(sum,1ll*C(m-i+j-1,m-i-1)*C(m-i+n-j-1,m-i)%mo);
			res=add(res,2ll*C(i+j-1,j-1)*C(n-j+i-1,n-j)%mo*sum%mo);
		}
	return res;
}
int main(){
	read(n);read(m);init();
	printf("%d\\n",sakura());
	return 0;
}
/*
C(i+j-1,j-1)C(n-j+i-1,n-j)C(m-i+k-1,k)C(m-i+n-k,n-k)
*/

谢谢！！！