[CF1486F]Pairs of Paths
Posted Tan_tan_tann
tags:
篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了[CF1486F]Pairs of Paths相关的知识，希望对你有一定的参考价值。
Pairs of Paths
题解
完了，跑得还没有常数大师快
首先我们可以证明一点，只有一下两种情况会使得两条路径有且只有一个交点。
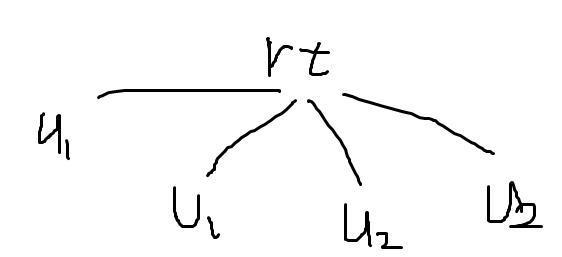
这种情况下
u
1
,
v
1
,
u
2
,
v
2
u_{1},v_1,u_2,v_2
u1,v1,u2,v2分别来自
r
t
rt
rt的不同儿子。
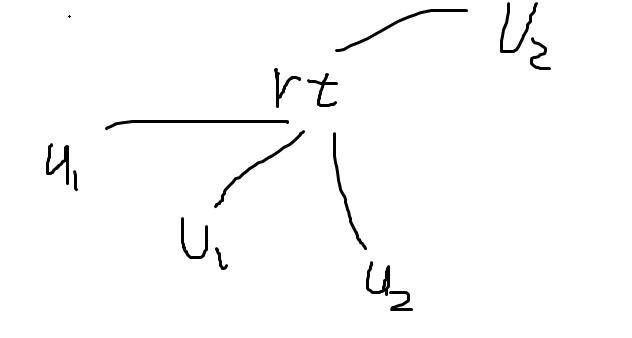
这种情况下，
u
1
,
v
1
,
u
2
u_1,v_1,u_2
u1,v1,u2都来自
r
t
rt
rt的某个儿子
v
2
v_2
v2是
r
t
rt
rt的一个祖先的某个儿孙或祖先它自己。
在这两种情况下，两条路径的的交点必定位于其中一条路径的
l
c
a
lca
lca处。
先考虑第一种情况，这种情况四个点都来自
r
t
rt
rt不同的儿子的子树上，如果有与
r
t
rt
rt本身相同的我们可以可以将其看作它的一个特殊的儿子。
我们可以将每条路径看作一个三元组
(
u
,
v
,
l
c
a
)
(u,v,lca)
(u,v,lca)，将这个三元组加在
l
c
a
lca
lca节点上。
如何统计与三元组
(
u
,
v
,
l
c
a
)
(u,v,lca)
(u,v,lca)有第一种形式相交的路径，我们可以先加上所有
l
c
a
lca
lca在这个儿子的路径，再容斥减去与其同一个儿子来源的路径。设
u
u
u来自儿子
a
a
a，
v
v
v来自儿子
b
b
b，那么与这条路径相交的节点有
t
o
t
a
l
−
s
u
m
u
−
s
u
m
v
+
s
u
m
u
,
v
total-sum_{u}-sum_{v}+sum_{u,v}
total−sumu−sumv+sumu,v。
注意有端点在这个
l
c
a
lca
lca的节点的路径，他在
l
c
a
lca
lca上的端点与别人相交是合法的，遇到这种情况就没必要进行对应的容斥。
那么对于第二种情况，很容易发现有一条路径的
l
c
a
lca
lca是另一条的祖先，也就是枚举到下面这个路径的
l
c
a
lca
lca时必定已经dfs上面这个路径的
l
c
a
lca
lca。
我们可以考虑利用dfs序建立一棵线段树，枚举到当前节点时将
l
c
a
lca
lca在这个节点上的线段的两个端点在线段树上
+
1
+1
+1，离开时
−
1
-1
−1。
这样在枚举到某个子节点时它的祖先的的线段必定都已加入，如果有一个端点在这个子节点的子树中，就必定与这个节点上的线段相交，那么对于这个节点上的线段，我们也可以采用容斥统计与它有第二种情况相交的线段数。
对于三元组
(
u
,
v
,
l
c
a
)
(u,v,lca)
(u,v,lca)，先加上线段树上
l
c
a
lca
lca子树区间内的和，再分别减去
u
,
v
u,v
u,v两者对应的儿子的子树内的区间和，就可以得到与它有第二种情况相交的线段数。
由于之前加入线段最多只有一个端点在
l
c
a
lca
lca的子树内，没必要进行容斥，直接加上
s
u
m
l
c
a
−
s
u
m
a
−
s
u
m
b
sum_{lca}-sum_{a}-sum_{b}
sumlca−suma−sumb即可。
同样需要注意有端点就是
l
c
a
lca
lca的线段的情况，避免减多了。
对于一条路径只有一个点的情况，我们需要特殊考虑一下，因为这种情况下只要经过这个点的线段就与它符合条件。
时间复杂度
O
(
n
l
o
g
n
)
O\\left(nlog\\,n\\right)
O(nlogn)。
妹儿的树状数组做法好像常数会小些，但复杂度是一样的
源码
话说为什么我现在都喜欢用dosaka来代替dfs呀
#include<bits/stdc++.h>
using namespace std;
#define MAXN 300005
#define lowbit(x) (x&-x)
#define reg register
#define fir first
#define sec second
typedef long long LL;
typedef unsigned long long uLL;
const LL INF=1000000000000LL;
const LL mo=1e9+7;
const LL inv2=5e8+4;
const LL jzm=2333;
const double Pi=acos(-1.0);
typedef pair<int,int> pii;
const double PI=acos(-1.0);
template<typename _T>
_T Fabs(_T x){return x<0?-x:x;}
template<typename _T>
void read(_T &x){
_T f=1;x=0;char s=getchar();
while(s>'9'||s<'0'){if(s=='-')f=-1;s=getchar();}
while('0'<=s&&s<='9'){x=(x<<3)+(x<<1)+(s^48);s=getchar();}
x*=f;
}
template<typename _T>
void print(_T x){if(x<0){x=(~x)+1;putchar('-');}if(x>9)print(x/10);putchar(x%10+'0');}
int n,m,head[MAXN],tot,dep[MAXN],f[MAXN][22],dfn[MAXN],idx;
LL ans;int sum[MAXN],val[MAXN],tr[MAXN<<2],ld[MAXN],rd[MAXN];
map<int,int>mp[MAXN];
struct ming{int a,b;};
vector<ming>vec[MAXN];
struct edge{int to,nxt;}e[MAXN<<1];
inline void addEdge(int u,int v){e[++tot]=(edge){v,head[u]};head[u]=tot;}
void dosaka(int u,int fa){
dep[u]=dep[fa]+1;f[u][0]=fa;dfn[u]=++idx;ld[u]=idx;
for(reg int i=1;i<20;i++)f[u][i]=f[f[u][i-1]][i-1];
for(reg int i=head[u];i;i=e[i].nxt)if(e[i].to!=fa)dosaka(e[i].to,u);rd[u]=idx;
}
int lca(int u,int v){
if(dep[u]>dep[v])swap(u,v);
for(reg int i=19;i>=0;i--)if(dep[f[v][i]]>=dep[u])v=f[v][i];
if(u==v)return u;
for(reg int i=19;i>=0;i--)if(f[u][i]!=f[v][i])u=f[u][i],v=f[v][i];
return f[u][0];
}
int FindFa(int u,int dp){for(reg int i=19;i>=0;i--)if(dp&(1<<i))u=f[u][i];return u;}
void insert(int rt,int l,int r,int ai,int aw){
if(l>r||l>ai||r<ai)return ;tr[rt]+=aw;
if(l==r)return ;int mid=l+r>>1;
if(ai<=mid)insert(rt<<1,l,mid,ai,aw);
else insert(rt<<1|1,mid+1,r,ai,aw);
}
int query(int rt,int l,int r,int al,int ar){
if(l>r||l>ar||r<al)return 0;int mid=l+r>>1;
if(al<=l&&r<=ar)return tr[rt];int res=0;
if(al<=mid)res+=query(rt<<1,l,mid,al,ar);
if(ar>mid)res+=query(rt<<1|1,mid+1,r,al,ar);
return res;
}
void dosaka1(int u,int fa){
for(reg int i=0;i<(int)vec[u].size();i++)insert(1,1,n,dfn[vec[u][i].a],1),insert(1,1,n,dfn[vec[u][i].b],1);
for(reg int i=head[u];i;i=e[i][CF403D]Beautiful Pairs of Numbers
题解CF#236(Div. 1) D-Beautiful Pairs of Numbers