求正数数组的最小不可组成和 --- 背包问题（动态规划）

Posted 2021-06-19 满眼*星辰

目录

• 求正数数组的最小不可组成和
• • 题目
  • 解题思路
  • 代码实现

求正数数组的最小不可组成和

题目

给定一个全是正数的数组arr，定义一下arr的最小不可组成和的概念： 1，arr的所有非空子集中，把每个子集内的所有元素加起来会出现很多的值，其中最小的记为min，最大的记为max； 2，在区间[min,max]上，如果有一些正数不可以被arr某一个子集相加得到，那么这些正数中最小的那个，就是arr的最小不可组成和； 3，在区间[min,max]上，如果所有的数都可以被arr的某一个子集相加得到，那么max+1是arr的最小不可组成和； 举例： arr = {3,2,5} arr的min为2，max为10，在区间[2,10]上，4是不能被任何一个子集相加得到的值中最小的，所以4是arr的最小不可组成和； arr = {3,2,4} arr的min为2，max为9，在区间[2,9]上，8是不能被任何一个子集相加得到的值中最小的，所以8是arr的最小不可组成和； arr = {3,1,2} arr的min为1，max为6，在区间[2,6]上，任何数都可以被某一个子集相加得到，所以7是arr的最小不可组成和； 请写函数返回arr的最小不可组成和。

链接：https://www.nowcoder.com/questionTerminal/296c2c18037843a7b719cf4c9c0144e4
来源：牛客网

解题思路

这是一个动态规划的01背包问题

根据承重和已有的重量种类阶段性计算当前承重时能够放入的重量

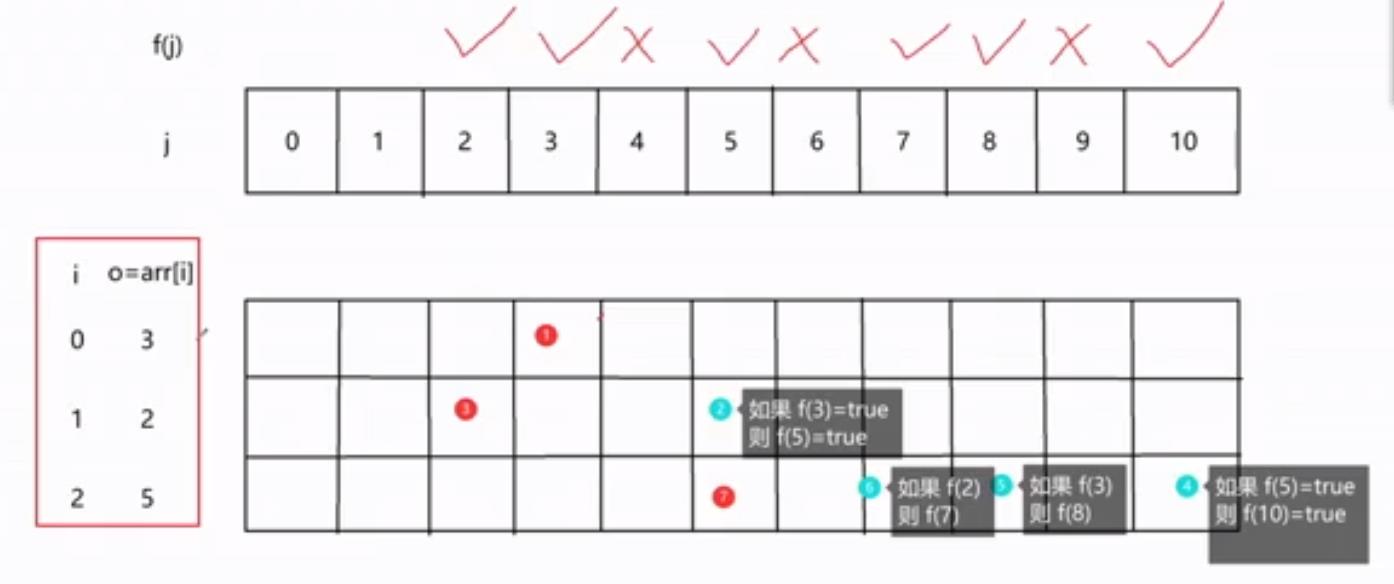
• 当数组中只有2重量的时候，背包承重从2-10都可以放入2的数值
• 当数组中放入2和3重量的时候，背包承重从5-10可以放入5，3-4放入3，2只能放入2
• 当数组中放入2，3，5重量时，背包承重10放入10，8-9放入8，7放入7，5-6放入5…

最终当每个承重与放入重量不同时，这个承重就是最小不可求和4

代码实现

    /**
     *  正数数组中的最小不可组成和
     *  输入：正数数组arr
     *  返回：正数数组中的最小不可组成和
     */
    public int getFirstUnFormedNum(int[] arr) {
        int min = Integer.MAX_VALUE;
        int max = 0;
        for(int i = 0; i < arr.length; i++) {
            max += arr[i];
            min = Math.min(min,arr[i]);
        }
        boolean[] form = new boolean[max+1];
        form[0] = true;
        for(int i = 0; i < arr.length; i++) {
            //逆序判断背包承重中能够放入的数据
            //当数组中只有2的时候，背包承重从2-10都可以放入2的数值
            //当数组中放入2和3的时候，背包承重从5-10可以放入5，3-4放入3，2只能放入2
            //当数组中放入2，3，5时，背包承重10放入10，8-9放入8，7放入7，5-6放入5...
            //dp[j-arr[i]]意思是背包承重为j时，如果已经放置了arr[i]的重量后还能放置的最大重量
            for(int j = max; j >= arr[i]; j--) {
                form[j] = form[j - arr[i]] || form[j];
            }
        }
        for(int i = min; i < form.length; i++) {
            if(!form[i]) {
                return i;
            }
        }
        return max+1;
    }