第四章 数学知识

Posted 2021-06-19 辉小歌

本文的所有内容模板都来自于y总

目录

• 试除法判定质数
• 试除法分解质因数
• 朴素筛法求素数
• 埃氏筛法求素数
• 线性筛法
• 试除法求所有约数
• 约数个数和约数之和
• 欧几里得算法
• 求欧拉函数
• 筛法求欧拉函数
• 快速幂

试除法判定质数

时间复杂度是根号n

bool is_prime(int x)
{
    if (x < 2) return false;
    for (int i = 2; i <= x / i; i ++ )
        if (x % i == 0)
            return false;
    return true;
}

试除法分解质因数

时间复杂度是 logn 到根号n 之间

void divide(int x)
{
    for (int i = 2; i <= x / i; i ++ )
        if (x % i == 0)
        {
            int s = 0;
            while (x % i == 0) x /= i, s ++ ;
            cout << i << ' ' << s << endl;
        }
    if (x > 1) cout << x << ' ' << 1 << endl;  //这是说明结果是 类似于 86 =2*43   43不可再分了这种情况
    cout << endl;
}

朴素筛法求素数

时间复杂度: O(nlogn)

int primes[N], cnt;     // primes[]存储所有素数
bool st[N];         // st[x]存储x是否被筛掉

void get_primes(int n)
{
    for (int i = 2; i <= n; i ++ )
    {
        if (st[i]) continue;
        primes[cnt ++ ] = i;
        for (int j = i + i; j <= n; j += i)
            st[j] = true;
    }
}

埃氏筛法求素数

时间复杂度: O(nloglogn)

int  cnt;     // 存储素数个数
bool hush[N];         // st[x]存储x是否被筛掉
for(int i=2;i<=n;i++)
    {
        if(!hush[i])
        {
            cnt++;
            for(int j=i+i;j<=n;j+=i) hush[j]=true;
        }
    }

线性筛法

你会发现: 用埃氏筛法的话，有一些数是筛了多遍的。
例： 6 用 2筛过一遍，用3又筛过一遍。

那么线性筛法就来了，它对于每一个数都只筛一遍是线性的，当要筛的数特别多的时候。
线性筛法几乎快埃氏筛法一倍的速度。
下面的总结来自于: Acwing的评论区，我从中摘抄了里面的精华。
线性筛法的原理:

• 核心:1~n内的合数只会被其最小质因子筛掉.
• 原理:1~n之内的任何一个合数一定会被筛掉,而且筛的时候只用最小质因子来筛,
  然后每一个数都只有一个最小质因子,因此每个数都只会被筛一次,因此线性筛法是线性的.

int primes[N], cnt;     // primes[]存储所有素数
bool st[N];         // st[x]存储x是否被筛掉

void get_primes(int n)
{
    for (int i = 2; i <= n; i ++ )
    {
        if (!st[i]) primes[cnt ++ ] = i;
        for (int j = 0; primes[j] <= n / i; j ++ )
        {
            st[primes[j] * i] = true;
            if (i % primes[j] == 0) break;
        }
    }
}

关于线性筛的解释:
枚举到i的最小质因子的时候就会停下来,即”if(i%primes[j]==0) break;”。
因为从小到大枚举的所有质数,所以当”i%primes[j]!=0”时,primes[j]一定小于i的最小质因子,
primes[j]一定是primes[j]i的最小质因子.
因为是从小到大枚举的所有质数,所以当”i%primes[j]==0”时,primes[j]一定是i的最小质因子,
而primes[j]又是primes[j]的最小质因子,因此primes[j]是iprimes[j]的最小质因子.
关于for循环的解释:
注:首先要把握住一个重点:我们枚举的时候是从小到大枚举的所有质数

• 1.当i%primes[j]==0时,因为是从小到大枚举的所有质数,所以primes[j]就是i的最小质因子,而primes[j]又是其本身
  primes[j]的最小质因子,因此当i%primes[j]==0时,primes[j]是primes[j]i的最小质因子.
• 2.当i%primes[j]!=0时,因为是从小到大枚举的所有质数,且此时并没有出现过有质数满足i%primes[j]==0,
  因此此时的primes[j]一定小于i的最小质因子,而primes[j]又是其本身primes[j]的最小质因子,
  所以当i%primes[j]!=0时,primes[j]也是primes[j]i的最小质因子.
• 3.综合1,2得知,在内层for循环里面无论何时,primes[j]都是primes[j]i的最小质因子,因此”st[primes[j]i]=true”
  语句就是用primes[j]i这个数的最小质因子来筛掉这个数.

for (int j = 0; primes[j] <= n / i; j ++)不需要写成 for (int j = 0; j < cnt && primes[j] <= n / i; j ++)理由:
如果 i 是合数，那它有最小质因子 prime[j]，所以循环会在枚举到 prime[j] 时 break 掉；
如果 i 是质数，则由于上面刚把 i 加到了 primes 数组中，所以 prime[j] 枚举到最后一个时正好等于 i，
所以也会 break 掉。因此 j 不会大于等于当前的 cnt

试除法求所有约数

vector<int> get_divisors(int x)
{
    vector<int> res;
    for (int i = 1; i <= x / i; i ++ )
        if (x % i == 0)
        {
            res.push_back(i);
            if (i != x / i) res.push_back(x / i);//避免  36  6*6 进入2个6的情况
        }
    sort(res.begin(), res.end());
    return res;
}

约数个数和约数之和

如果 N = p1^c1 * p2^c2 * ... *pk^ck
约数个数： (c1 + 1) * (c2 + 1) * ... * (ck + 1)
约数之和： (p1^0 + p1^1 + ... + p1^c1) * ... * (pk^0 + pk^1 + ... + pk^ck)

约数个数公式的解析:

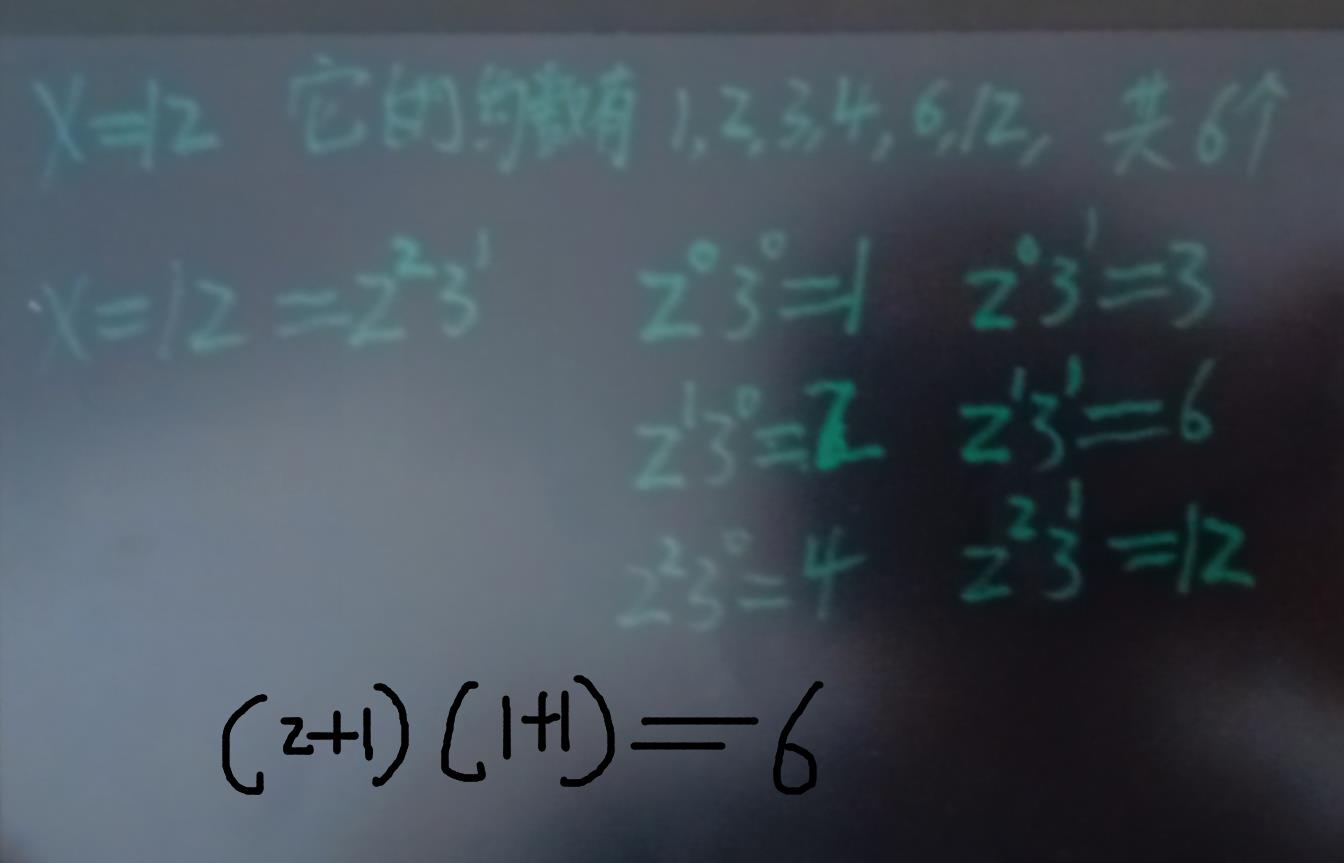
约数之和公式解析:

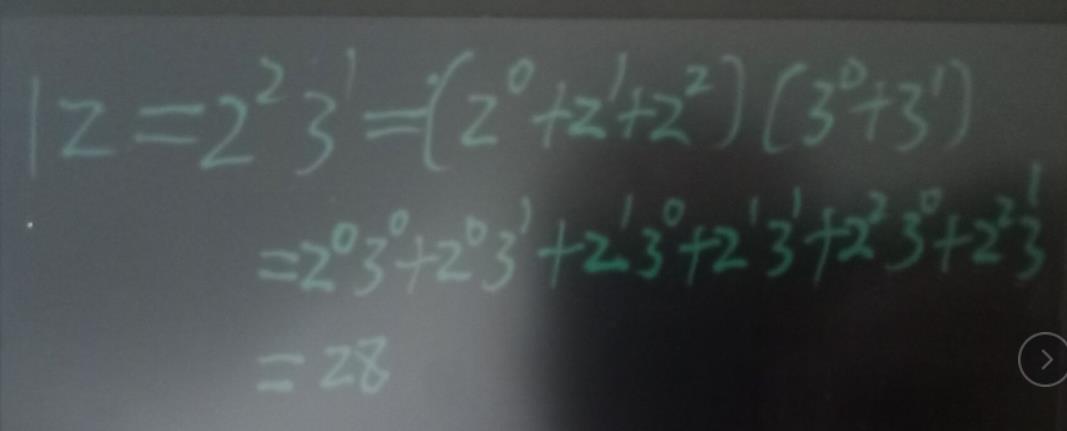
欧几里得算法

int gcd(int a, int b)
{
    return b ? gcd(b, a % b) : a;
} 

求欧拉函数

int phi(int x)
{
    int res = x;
    for (int i = 2; i <= x / i; i ++ )
        if (x % i == 0)
        {
            res = res / i * (i - 1);
            while (x % i == 0) x /= i;
        }
    if (x > 1) res = res / x * (x - 1);

    return res;
}

筛法求欧拉函数

int primes[N], cnt;     // primes[]存储所有素数
int euler[N];           // 存储每个数的欧拉函数
bool st[N];         // st[x]存储x是否被筛掉


void get_eulers(int n)
{
    euler[1] = 1;
    for (int i = 2; i <= n; i ++ )
    {
        if (!st[i])
        {
            primes[cnt ++ ] = i;
            euler[i] = i - 1;
        }
        for (int j = 0; primes[j] <= n / i; j ++ )
        {
            int t = primes[j] * i;
            st[t] = true;
            if (i % primes[j] == 0)
            {
                euler[t] = euler[i] * primes[j];
                break;
            }
            euler[t] = euler[i] * (primes[j] - 1);
        }
    }
}

快速幂

迭代法:

求 m^k mod p，时间复杂度 O(logk)。

int qmi(int m, int k, int p)
{
    int res = 1 % p, t = m;
    while (k)
    {
        if (k&1) res = res * t % p;
        t = t * t % p;
        k >>= 1;
    }
    return res;
}

递归法：

#include<cstdio>
#include<iostream>
using namespace std;
typedef long long int ll;
ll f(ll a,ll b,ll c)
{
    if(!b) return 1;
    ll res=f(a,b>>1,c);
    if(b&1) return a*res%c*res%c;
    else return res*res%c;
}
int main(void)
{
    int n; scanf("%d",&n);
    while(n--)
    {
        ll a,b,c; scanf("%lld%lld%lld",&a,&b,&c);
        cout<<f(a,b,c)<<endl;
    }
    return 0;
}