线性规划标准型转化及单纯性算法之线性规划网络流

Posted 2021-06-19 11biscuits

线性规划问题

（1） 确定决策变量
（2） 确定目标函数
（3） 找出约束条件
（4） 求最优解

简单问题
例:

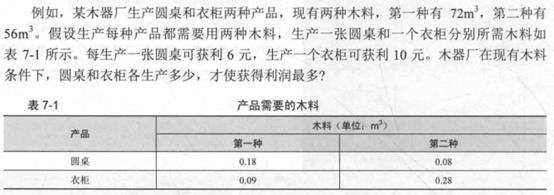
图片来源:《趣学算法》陈小玉-人民邮电出版社

 变量满足约束条件的一组值称为线性规划的一个可行解
 所有可行解构成集合称为线性规划问题的可行区域
 使得目标函数取得极值得可行解称为最优解
 在最优解处目标函数的值称为最优值

线性规划问题解的情况
有唯一最优解 有无数个最优解 没有最优解

线性规划标准型

线性规划标准型转化方法

单纯性算法

基本变量：
每个约束条件中的系数为正且只出现在一个约束中的变量。
非基本变量:
除基本变量外的变量全部为非基本变量。
基本可行解：
满足标准形式约束条件的可行解称为基本可行解。
检验数:
目标函数中非基本变量的系数。

线性规划基本定理：
定理1：最优解判别定理
若目标函数中关于非基本变量的所有系数(检验数Cj )小于等于0，则当前基本可行解就是最优解。
定理2：无穷多最优解判别定理
若目标函数中关于非基本变量的所有检验数小于等于0，同时存在某个非基本变量的检验数等于0，则线性规划问题有无穷多个最优解。
定理3：无界解定理
如果某个检验数Cj大于0，而Cj所对应的列向量的各分量a1j,a2j,…,amj都小于等于0，则线性规划问题有无界解。
算法步骤
（1） 建立初始单纯形表


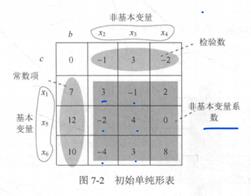
（2） 判断是否得到最优解

（3） 选入基变量


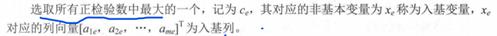
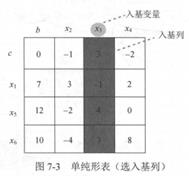
（4） 选离基变量


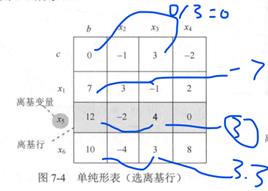
（5） 换基变换


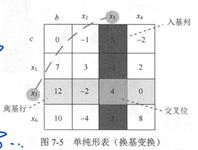
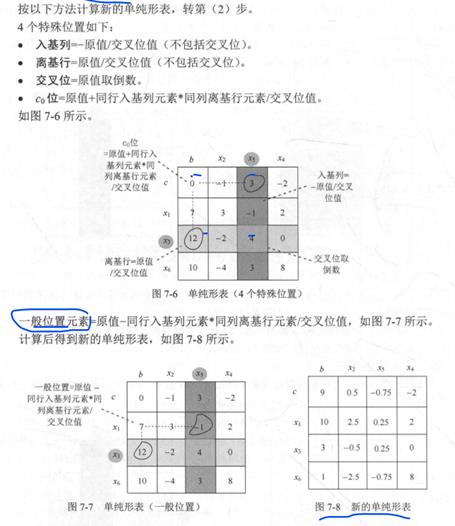
（6） 计算新的单纯形表

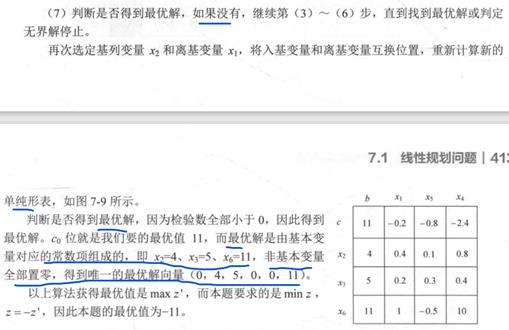
（7） 判断是否得到最优解