523. 连续的子数组和

Posted 2021-06-19 Rainbowman 0

通过这道题，了解到了一个很有用的数学知识：

若 (a - b) 可以被k整除
则a % k = b % k

即，若a-b是k的倍数，则a和b分别除以k得到的余数相同。

题目

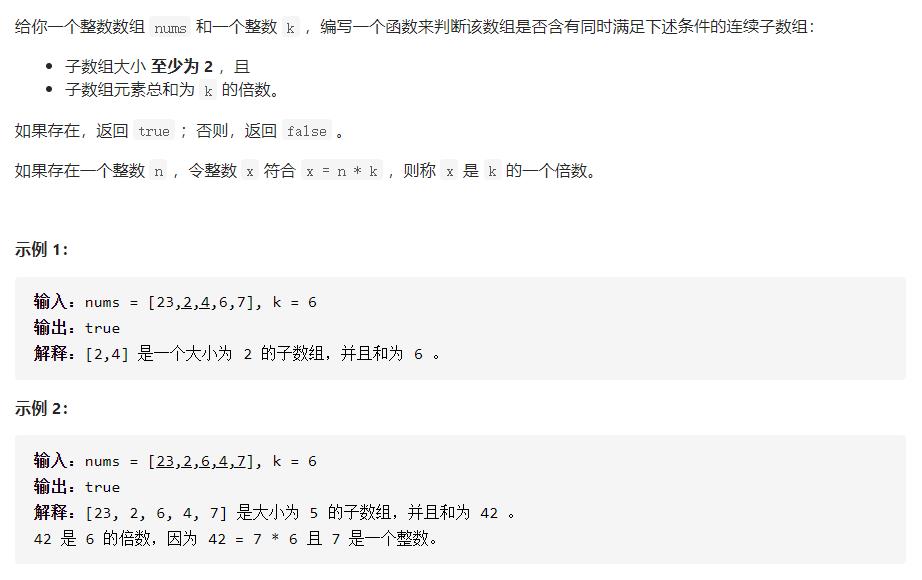
题解：

class Solution {
public:
    bool checkSubarraySum(vector<int>& nums, int k) {
        if(nums.empty())  return false;
        if(nums.size()<2)  return false;
        unordered_map<int, int> umap;  // key: 余数 value:出现次数
        umap[0] = -1;
        int sum = 0;
        // 构造前缀和
        for(int i=0; i<nums.size(); i++){
            sum += nums[i];
            if(umap.count(sum%k)){
                if(i-umap[sum%k]>=2)  return true;
            }
            else  umap[sum%k] = i;
        }

        return false;
    }
};

总结：

这道题的思路是前缀和+上述性质+哈希表

（1）纯暴力：

两个循环，每次还要计算从i到j的和，故O(n³)

（2）前缀和：

先用O(n)算出前缀和，preSum[i]表示前i个元素的和，然后用两层循环暴力检测是否存在(preSum[i] - preSum[j]) % k == 0的情况，故整体为O(n²)

（3）前缀和+上述性质+哈希表：

（2）的方法之所以要用O(n²)，是因为要求(preSum[i] - preSum[j]) % k == 0， 即要求(preSum[i] - preSum[j])是否能被k整除。
这就可以用到上述性质了，转换成preSum[i]%k是否和preSum[j]%k相等，这样就可以只有一遍遍历解决了。时间复杂度优化到O(n)。

真是妙啊~