代数57 ----平面直角坐标变换
Posted 炫云云
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了代数57 ----平面直角坐标变换相关的知识,希望对你有一定的参考价值。
本节内容:
**1、**理解平面直角坐标的平移和旋转变换公式,理解移轴和转轴不改变二次曲线的形状,会对平面二次曲线做移轴和转轴变换
**2、**了解平面直角坐标的伸缩变换,理解伸缩会改变平面二次曲线的形状在不同的平面直角坐标系下,点、向量与曲线有不同的代数表示.
特别,对于平面二次曲线及其方程,有两个问题值得考虑:
KaTeX parse error: Expected '{', got '\\textcolor' at position 1: \\̲t̲e̲x̲t̲c̲o̲l̲o̲r̲{##df0030}{#1} 对平面二次曲线,如何选取合适的坐标系,得到形式简单的方程?
(—— 平面二次曲线方程的化简)
\\tag{—— 平面二次曲线方程的化简}
(—— 平面二次曲线方程的化简)
KaTeX parse error: Expected '{', got '\\textcolor' at position 1: \\̲t̲e̲x̲t̲c̲o̲l̲o̲r̲{##df0030}{#1} 在平面二次曲线方程中,哪些量是与坐标的选取无关的?
(—— 平面二次曲线的不变量)
\\tag{—— 平面二次曲线的不变量}
(—— 平面二次曲线的不变量)
坐标的选取
⇒
\\large{\\Rightarrow}
⇒ 平面直角坐标变换:平移、旋转、伸缩
例如,以下三个不同方程表示的曲线是否是同一几何曲线 ?
C
1
:
x
2
−
y
2
=
4
,
C
2
:
x
2
−
y
2
=
4
x
,
C
3
:
x
y
=
2.
C_1:x^2-y^2=4,C_2:x^2-y^2= 4x ,C_3:xy = 2.
C1:x2−y2=4,C2:x2−y2=4x,C3:xy=2.
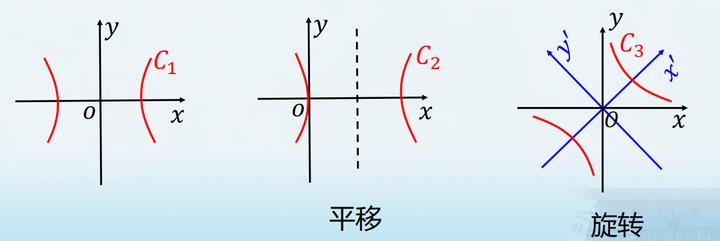
平面直角坐标的平移
在平面上,平行移动平面直角坐标系,称为平面直角坐标系的 平 移 \\Large\\color{#70f3ff}{\\boxed{\\color{green}{平移}}} 平移 ,简称 移 轴 \\Large\\color{#70f3ff}{\\boxed{\\color{green}{移轴}}} 移轴 .
特点:
- 坐标轴的方向保持不变;
- 原点位置发生改变.
问题:移轴后,平面上点的坐标如何改变?
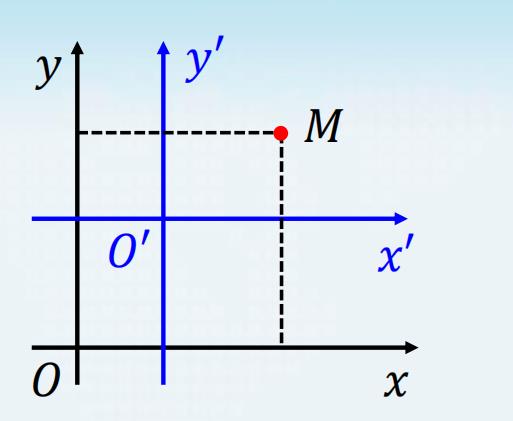
平 面 直 角 坐 标 的 平 移 变 换 公 式 \\large\\color{#70f3ff}{\\boxed{\\color{brown}{平面直角坐标的平移变换公式 } }} 平面直角坐标的平移变换公式
设 𝑂′ 在旧坐标系 𝑂𝑥𝑦 下的坐标为 𝑂 ′ ( 𝑥 0 , 𝑦 0 ) 𝑂′(𝑥_0, 𝑦_0) O′(x0,y0) .
点 𝑀 在旧坐标系 𝑂𝑥𝑦 下的坐标为 𝑀 ( 𝑥 , 𝑦 ) 𝑀 (𝑥, 𝑦) M(x,y) , 在新坐标系 𝑂′𝑥′𝑦′ 下的坐标为 𝑀 ( 𝑥 ′ , 𝑦 ′ ) 𝑀 (𝑥′, 𝑦′) M(x′,y′) .
则 { x = 𝑥 ′ + 𝑥 0 y = y ′ + y 0 — — 平 面 直 角 坐 标 的 移 轴 公 式 \\begin{cases} x= 𝑥′ + 𝑥_0\\\\ y= y′ + y_0 \\end{cases}\\color{red}{——平面直角坐标的移轴公式} {x=x′+x0y=y′+y0——平面直角坐标的移轴公式
⇒ ( x y ) = ( x ′ y ′ ) + ( x 0 y 0 ) \\Rightarrow \\binom{x}{y}=\\binom{x'}{y'}+\\binom{x_0}{y_0} ⇒(yx)=(y′x′)+(y0x0)
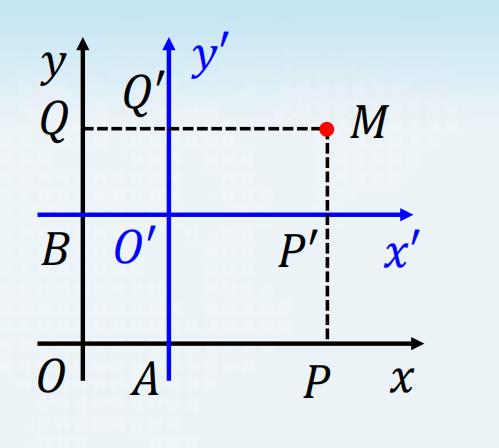
𝑂𝑃 = 𝐴𝑃 + 𝑂𝐴 = 𝑂′𝑃′ + 𝑂𝐴 𝑂𝑄 = 𝐵𝑄 + 𝑂𝐵 = 𝑂′𝑄′ + 𝑂𝐵
$\\color{red}{移轴逆变换公式:} $ { 𝑥 ′ = x − 𝑥 0 y ′ = y − y 0 \\begin{cases} 𝑥′ = x- 𝑥_0\\\\ y′= y- y_0 \\end{cases} {x′=x−x0y′=y−y0
⇒ ( x y ) = ( x ′ y ′ ) + ( − x 0 − y 0 ) \\Rightarrow \\binom{x}{y}=\\binom{x'}{y'}+\\binom{-x_0}{-y_0} ⇒(yx)=(y′x′)+(−y0−x0)
几何解释: 𝑂 𝑥 𝑦 𝑂𝑥𝑦 Oxy 看成是 𝑂 ′ 𝑥 ′ 𝑦 ′ 𝑂′𝑥′𝑦′ O′x′y′ 平移得到的, 原点𝑂在𝑂′𝑥′𝑦′的坐标为 𝑂 ( − 𝑥 0 , − 𝑦 0 ) 𝑂 (−𝑥_0, −𝑦_0) O(−x0,−y0) .
例1
用移轴化简方程 C : x 2 + y 2 − 2 x + 4 y − 4 = 0 C:x^2+y^2-2x+4y -4= 0 C:x2+y2−2x+4y−4=0 ,并画出它的图形.
【解】 配方整理得 ( 𝑥 − 1 ) 2 + ( 𝑦 + 2 ) 2 = 9 (𝑥 − 1)^2+(𝑦 + 2)^2= 9 (x−1)2+(y+2)2=9
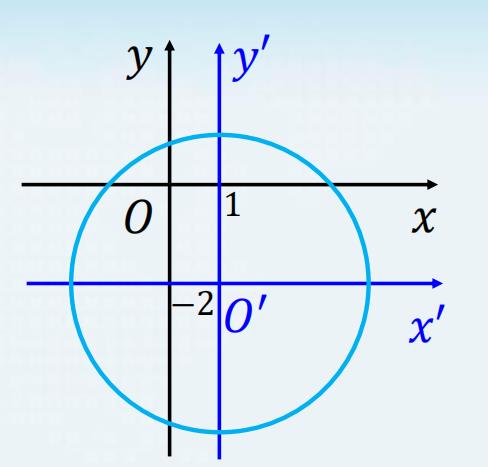
圆心 𝑂′(1, −2)
令 { 𝑥 ′ = x − 1 y ′ = y + 2 \\begin{cases} 𝑥′ = x- 1\\\\ y′= y+2 \\end{cases} {x′=x−1y′=y+2 ,或 { x = 𝑥 ′ + 1 y = y ′ − 2 \\begin{cases} x= 𝑥′ +1\\\\ y= y′ -2 \\end{cases} {x=x′+1y=y′−2
得 C : x ′ 2 + y ′ 2 = 9 C: x'^2 +y'^2= 9 C:x′2+y′2=9 .这是一个半径为3的圆.
【注】 移轴
以上是关于代数57 ----平面直角坐标变换的主要内容,如果未能解决你的问题,请参考以下文章