永磁同步电机的直接转矩控制一一一滑模控制器改进DTC
Posted 昔时扬尘处
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了永磁同步电机的直接转矩控制一一一滑模控制器改进DTC相关的知识,希望对你有一定的参考价值。
永磁同步电机的直接转矩控制(三)一一一滑模控制器改进DTC
目录
0研究背景
写在前面:
1.本代码基于MATLAB2019a版本,低版本或者不同版本可能会报错,mdl文件或slx文件打开可能会失败;
2.本博客附上仿真模型并详细介绍各个部分的搭建,如果转载请注明出处;
3.如果本博客恰巧与您的研究有所关联,欢迎您的咨询qq1366196286。
1改进直接转矩控制的模型搭建
传统DTC的实现可参考之前的博客永磁同步电机的直接转矩控制(一)一一一DTC仿真模型的搭建
其中,传统DTC存在一些缺点,为此本博客对传统DTC进行改进。

如前所述,传统DTC采用两个Bang-bang控制器分别对转矩和磁链幅值进行控制,响应快速,对系统参数摄动和外干扰鲁棒性强,但存在较大的磁链和转矩脉动,逆变器开关频率不恒定,低速时系统难以精确控制,以及因转矩脉动引起的高频噪声等问题。传统DTC中磁链和转矩脉动过大是因逆变器的实际开关频率不够高,从而导致一个数字控制周期中所选用的有效电压矢量无法与期望的电压矢量一致。然而,开关频率过大也会导致开关损耗加大。针对这些问题,可采取以下几种方法来改进传统DTC:
1.对传统DTC的开关表加以改进,如增加零电压矢量和矢量细分等。以及运用空间电压矢量调制方法使逆变器开关频率恒定,以减小转矩脉动圆。采用先进的控制器替换Bang-bang控制器。
2.采取滑模控制器进行改进。利用基于滑模控制(SMC)的DTC,以期解决传统DTC存在的转矩和磁链脉动较大、逆变器开关频率不恒定等问题。
3.针对功率变换器采取多电平控制,通过多个空间电压矢量作用于电机,使磁链、转矩平滑,但这增加了系统硬件成本和复杂性。
本博客采取第二种方法对传统DTC进行改进,以及通过SVPWM实现对PWM的生成。以下详细介绍实现过程及仿真实现。
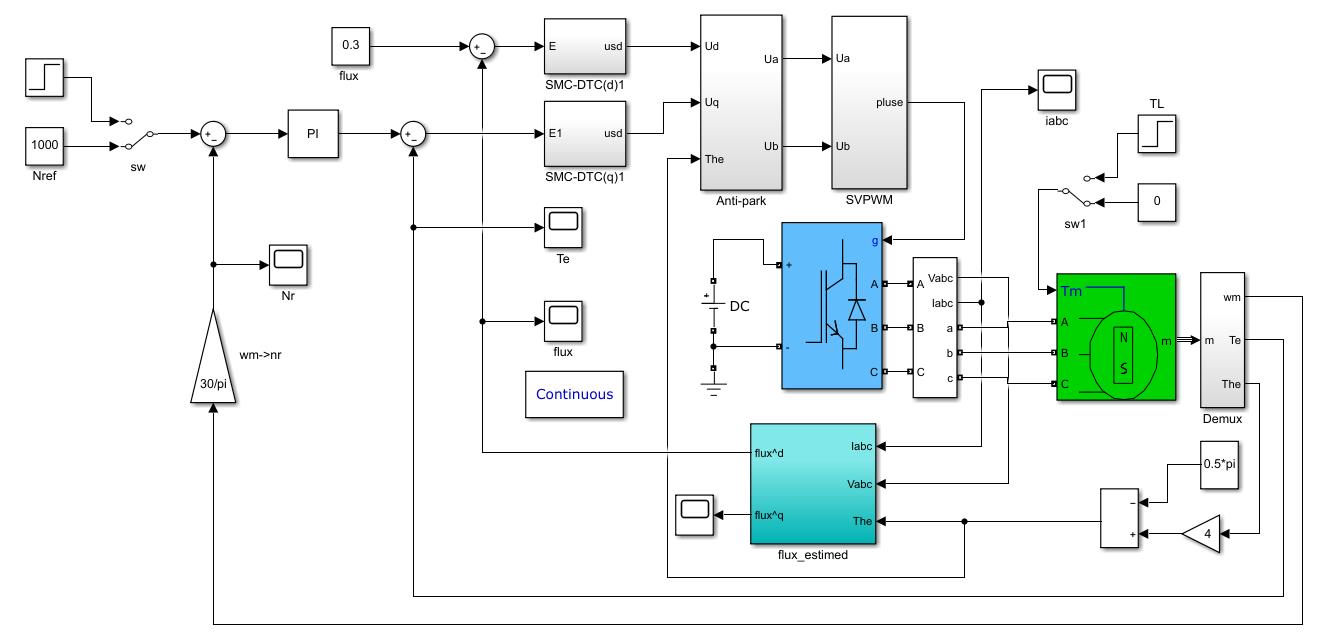
图1 滑模控制器的改进直接转矩控制Simulink仿真图
2改进直接转矩控制的模型搭建
2.1磁链控制器的设计
为了获得磁链控制器的表达式,定义磁链的滑模面函数为
s ϕ = ψ r ∗ − ψ r s_{\\phi}=\\psi_{\\mathrm{r}}^{*}-\\psi_{\\mathrm{r}} sϕ=ψr∗−ψr
利用基于super-twisting算法的二阶滑模控制基本原理,此时磁链控制器的表达式为
u d ∗ = K p ∣ s ψ ∣ r sgn ( s ψ ) + u s d u_{d}^{*}=K_{\\mathrm{p}}\\left|s_{\\psi}\\right|^{r} \\operatorname{sgn}\\left(s_{\\psi}\\right)+u_{\\mathrm{sd}} ud∗=Kp∣sψ∣rsgn(sψ)+usd
d d t u s d = K i sgn ( s ψ ) \\frac{\\mathrm{d}}{\\mathrm{d} t} u_{s d}=K_{\\mathrm{i}} \\operatorname{sgn}\\left(s_{\\psi}\\right) dtdusd=Kisgn(sψ)
其中:r为0,Kp,Ki>0,为待设计参数。
2.2磁链控制器的仿真模型
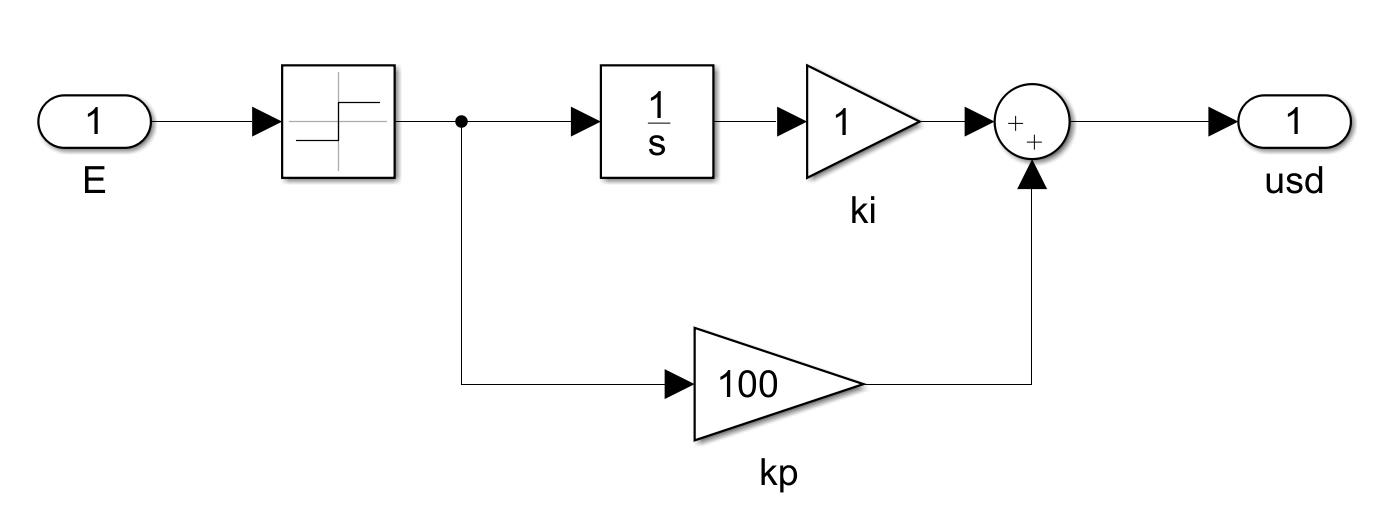
图2 磁链控制器的Simulink仿真图
2.3转矩控制器的设计
假设定子磁链 ψ r \\psi_{\\mathrm{r}} ψr的幅值为一常数,此时电磁转矩 T e T_{\\mathrm{e}} Te的微分方程可表示为:
d d t T e = 3 2 p n ψ I d d t i q \\frac{\\mathrm{d}}{\\mathrm{d} t} T_{\\mathrm{e}}=\\frac{3}{2} p_{\\mathrm{n}} \\psi_{\\mathrm{I}} \\frac{\\mathrm{d}}{\\mathrm{d} t} i_{q} dtdTe=23pnψIdtdiq
为了获得转矩控制器的表达式,定义转矩的滑模面函数为:
s T = T e ∗ − T c s_{T}=T_{\\mathrm{e}}^{*}-T_{\\mathrm{c}} sT=Te∗−Tc
同样利用基于super-twisting算法的二阶滑模控制基本原理,此时转矩控制器的表达式为:
u q ∗ = K p ∣ s T ∣ r sgn ( s T ) + u s q u_{q}^{*}=K_{\\mathrm{p}}\\left|s_{T}\\right|^{r} \\operatorname{sgn}\\left(s_{T}\\right)+u_{\\mathrm{s} q} uq∗=Kp∣sT∣rsgn(sT)+usq
d d t u s q = K i sgn ( s T ) \\frac{\\mathrm{d}}{\\mathrm{d} t} u_{\\mathrm{sq}}=K_{\\mathrm{i}} \\operatorname{sgn}\\left(s_{T}\\right) dtdusq=Kisgn(sT)
其中:r为0,Kp,Ki>0,为待设计参数。
2.4转矩控制器的仿真模型
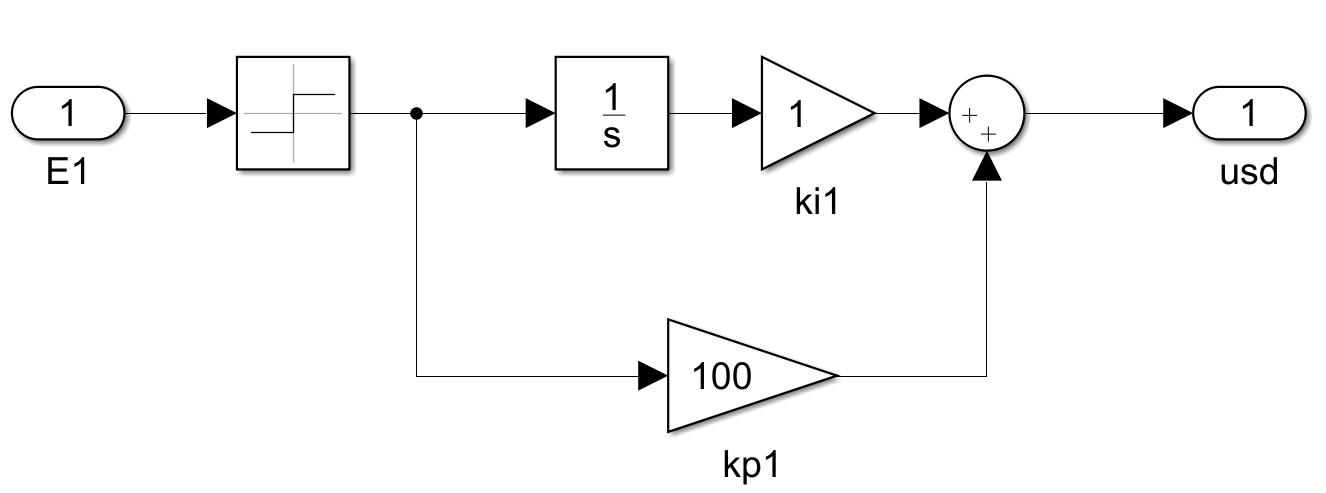
图3 转矩控制器的Simulink仿真图
2.5SVPWM的实现及仿真
将转矩控制器和磁链控制器分别计算所得的d-q轴电压量,经过反park变换后得到SVPWM所需要的α-β轴的参考电压矢量。
具体的实现过程及仿真模型搭建,可参考永磁同步电机的矢量控制策略(七)一一一SVPWM控制
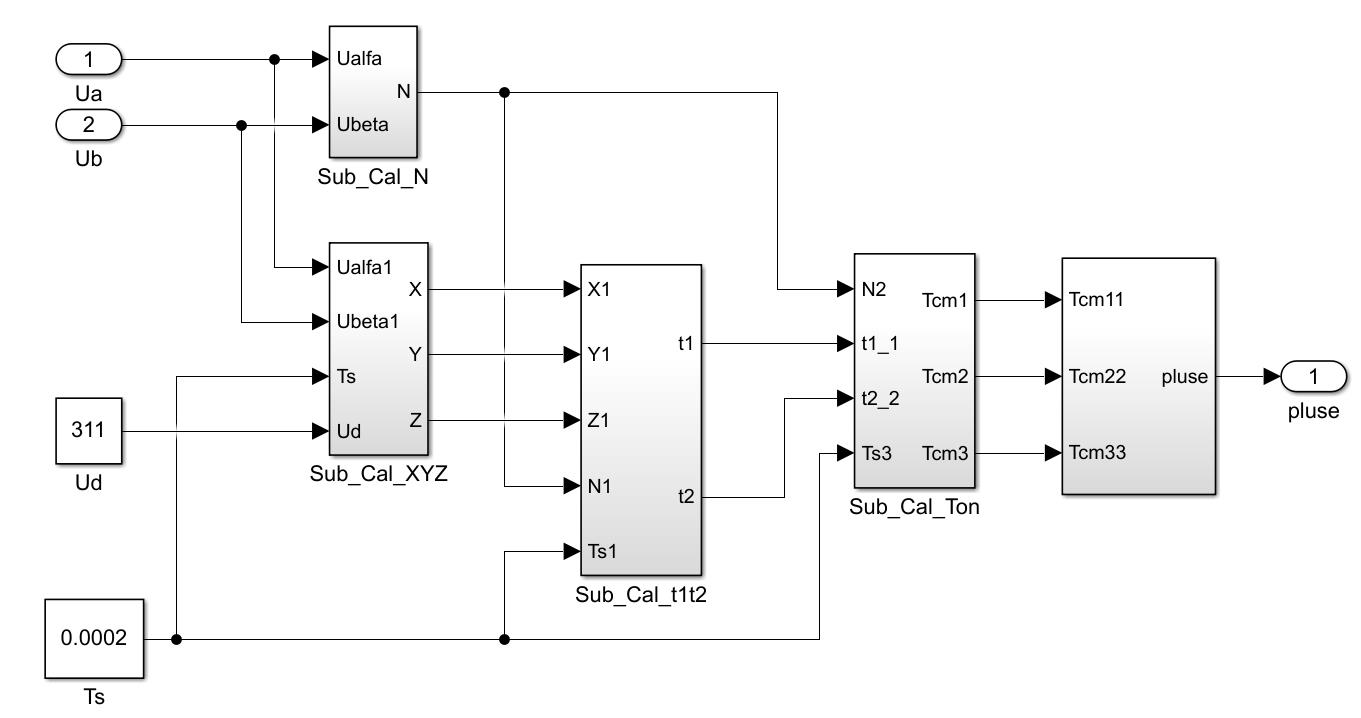
图4 SVPWM的Simulink仿真图
2.6磁链的估算模型
转矩和磁链的反馈信号,其中转矩是直接通过采集端并通过低通滤波器得到。然而,磁链是通过磁链的估算模型运用相电压、相电流间接计算所得。
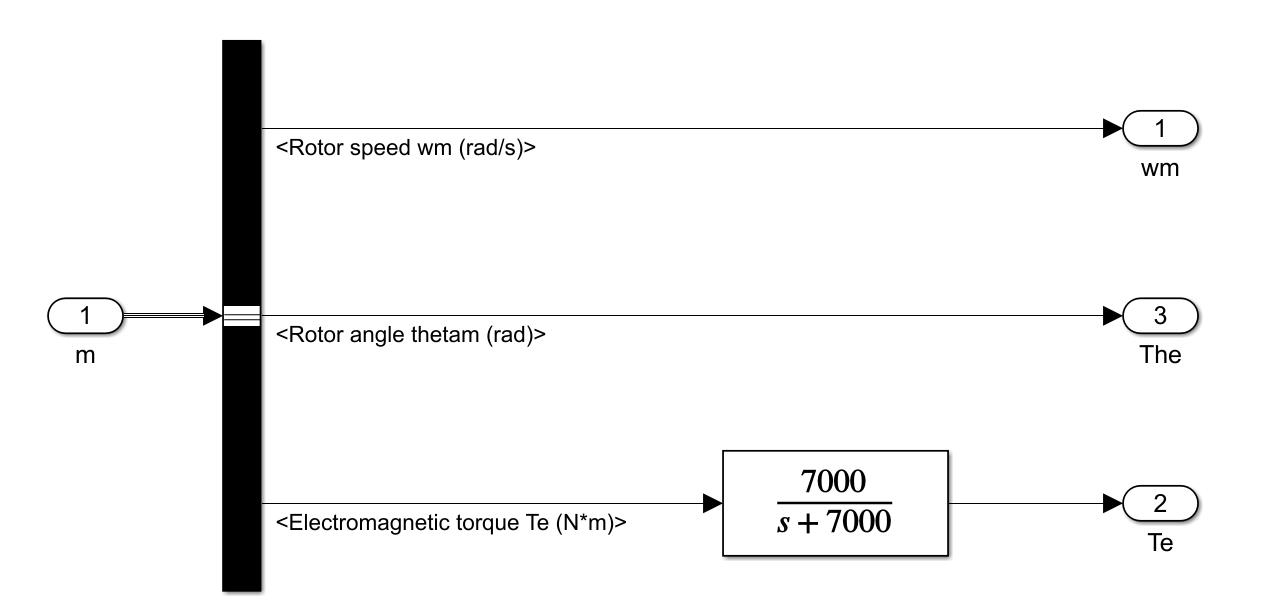
图5 转矩反馈信号的Simulink仿真图
为了控制电机就需要得到其磁链方程,其磁链方程的矢量形式为:
{
ψ
d
=
∫
u
d
−
R
s
i
d
d
t
ψ
q
=
∫
u
q
−
R
s
i
q
d
t
∣
ψ
s
∣
=
ψ
d
2
+
ψ
q
2
\\left\\{\\begin{array}{l}\\psi_{\\mathrm{d}}=\\int u_{\\mathrm{d}}-R_{\\mathrm{s}} i_{\\mathrm{d}} \\mathrm{d} t \\\\ \\psi_{\\mathrm{q}}=\\int u_{\\mathrm{q}}-R_{\\mathrm{s}} i_{\\mathrm{q}} \\mathrm{d} t \\\\ \\left|\\psi_{\\mathrm{s}}\\right|=\\sqrt{\\psi_{\\mathrm{d}}^{2}+\\psi_{\\mathrm{q}}^{2}}\\end{array}\\right.
⎩⎪⎨⎪⎧ψd=∫ud−Rsiddtψq=∫uq−Rsiqdt∣ψs∣=ψd2+ψq2
式中Rs为定子相电阻,ud、uq和id、iq分别为d-q轴的定子电压和电流,然定子磁链的位置则可通过d-q轴的分量和它们的正负号来决定。
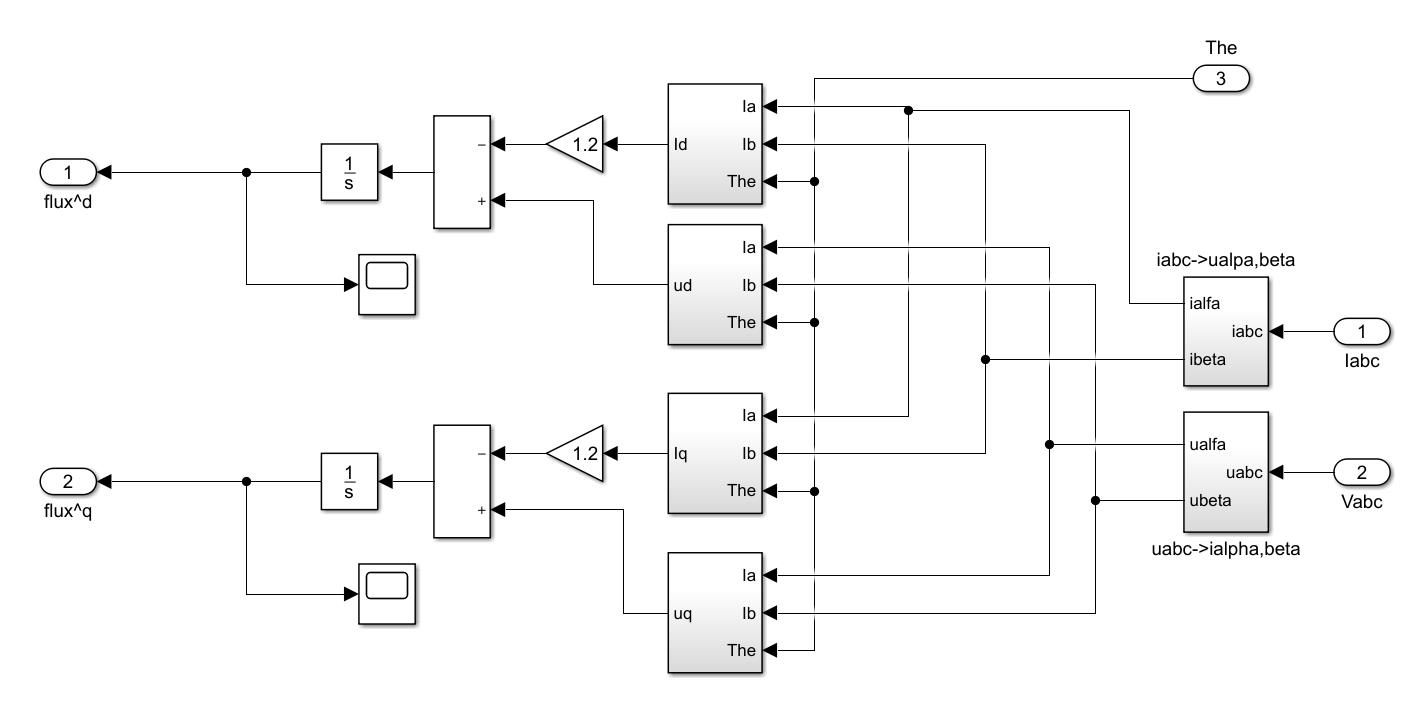
图6 磁链反馈信号的Simulink仿真图
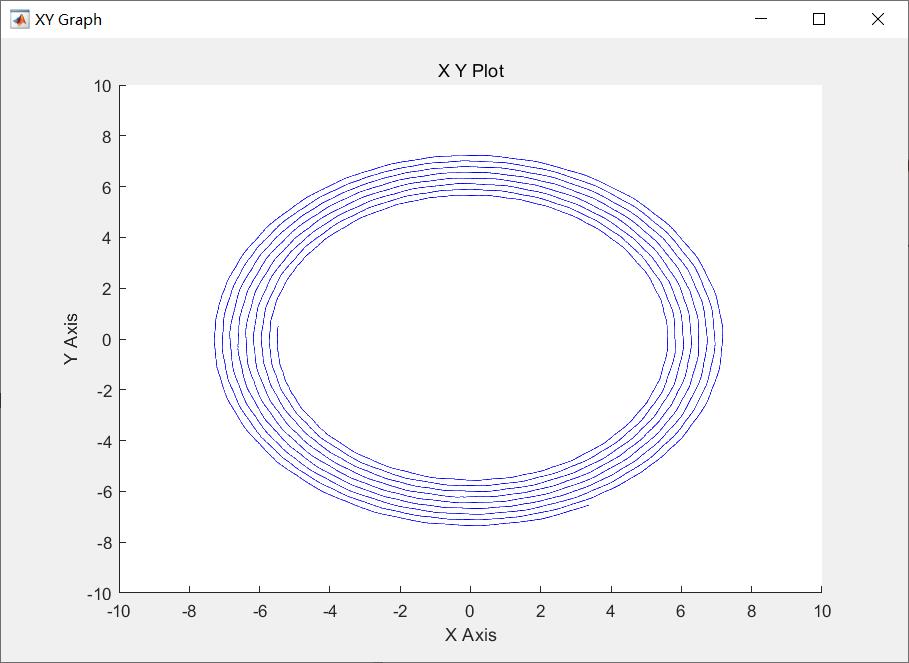
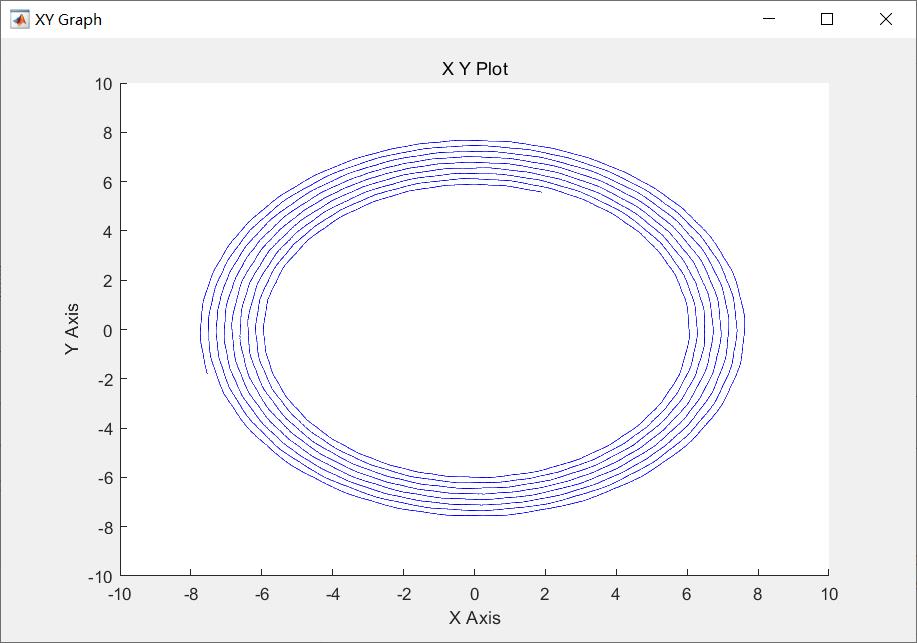
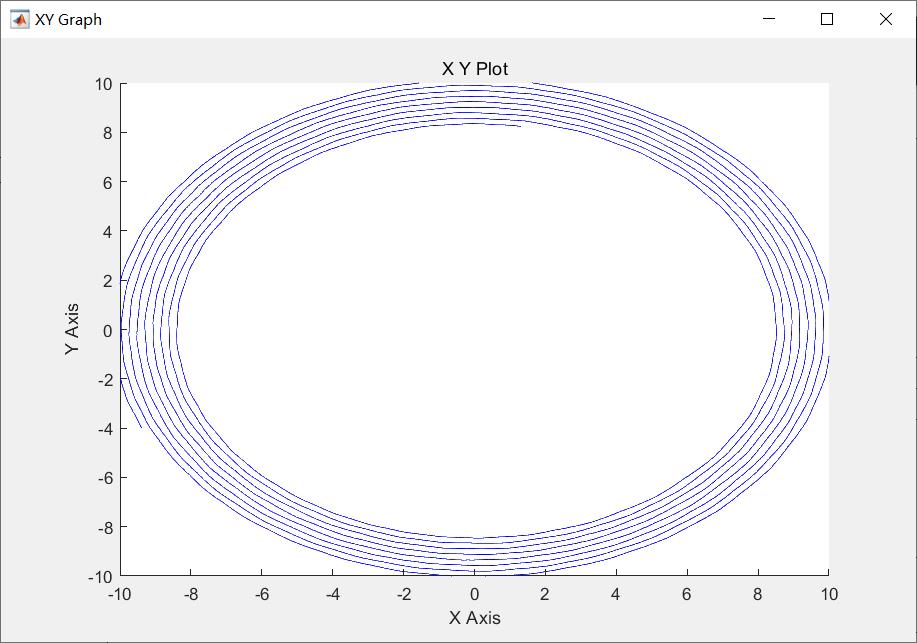
图7 a-β轴上的合成圆形磁链
ps:这里提个小问题:为什么改进后DTC的圆形磁链是同心圆,圆形磁链一直在增大?而不是像上一篇博文中的圆形磁链?
#可以在评论区写下你的想法与答案哦!
3改进直接转矩控制的仿真分析
3.1空载工况下
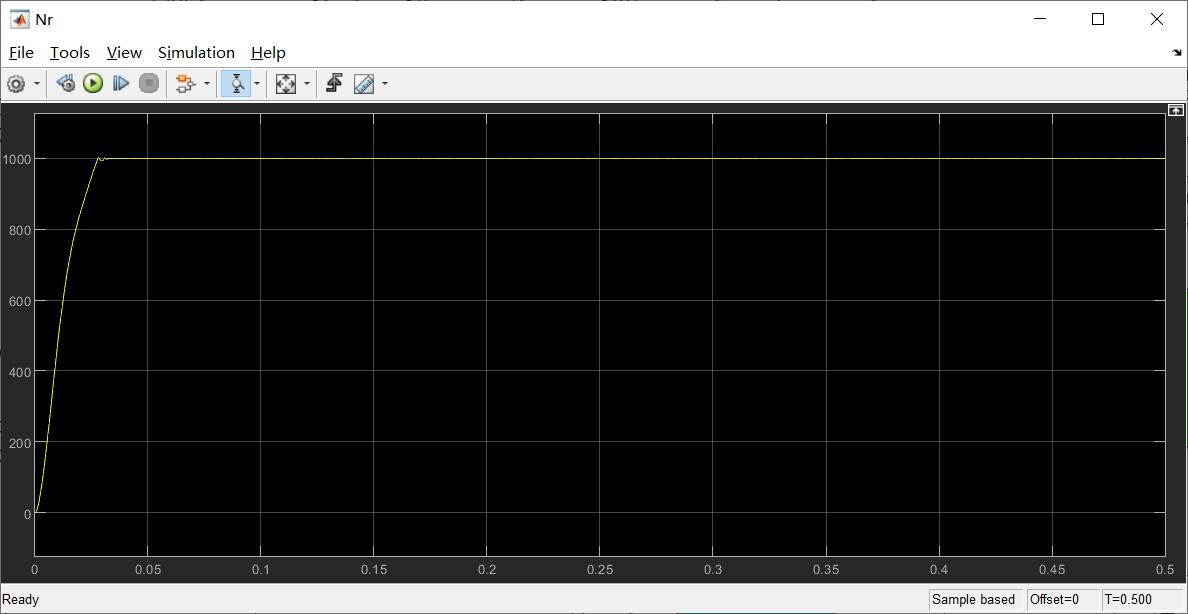
(1)转速响应
转速为阶跃转速,0s由0 r/min阶跃上升至1000 r/min.
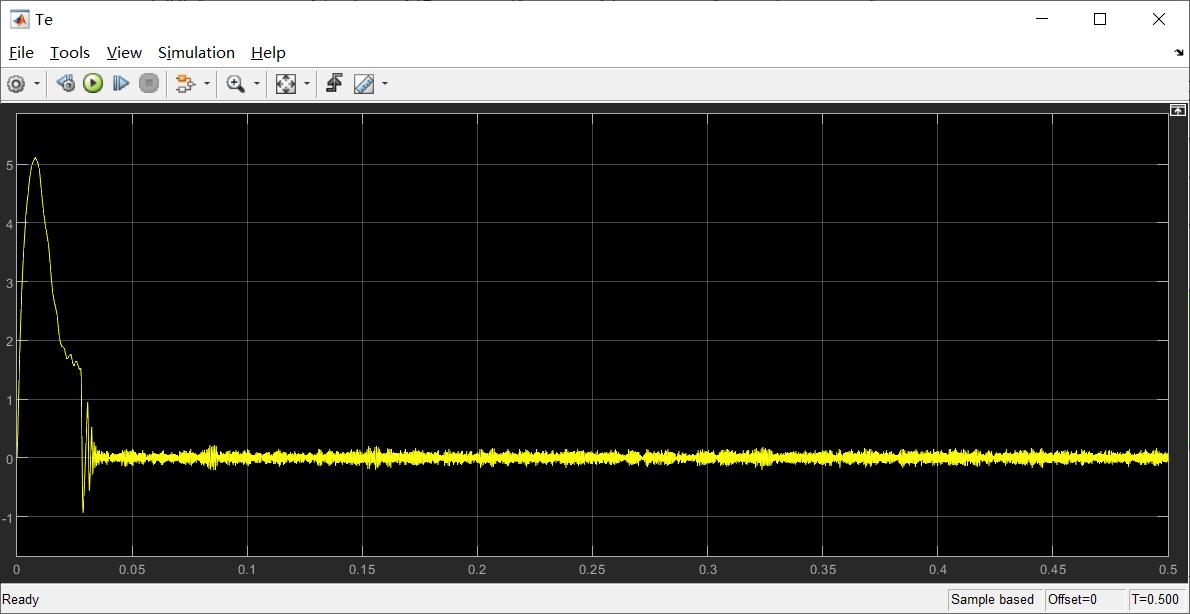
(2)转矩响应
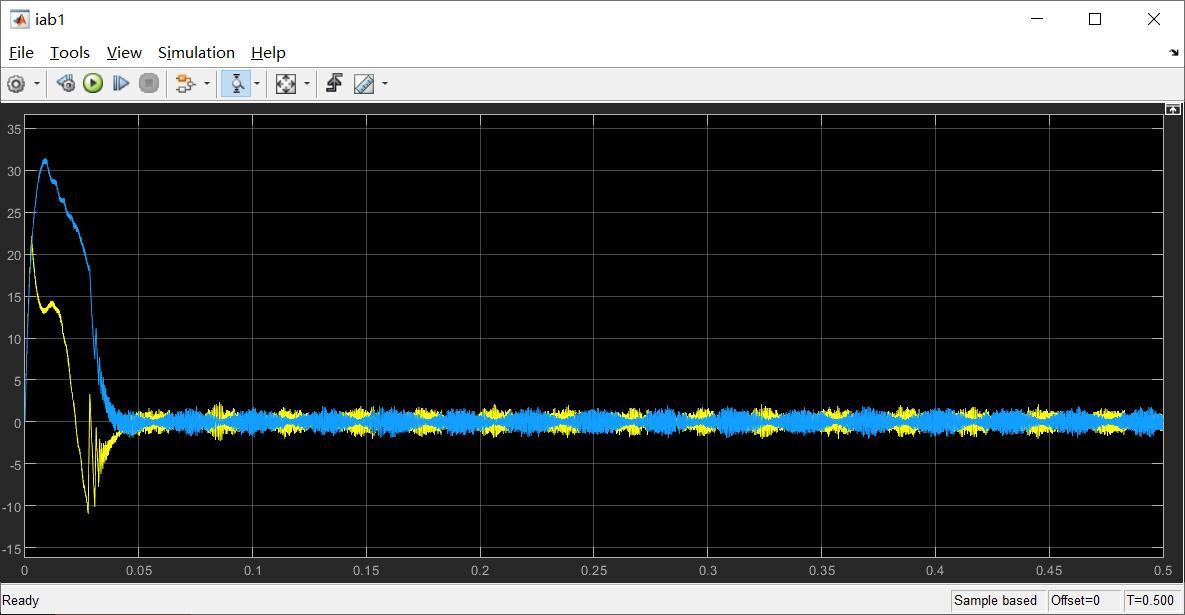
(3)a-β轴的电流响应
(4)磁链响应
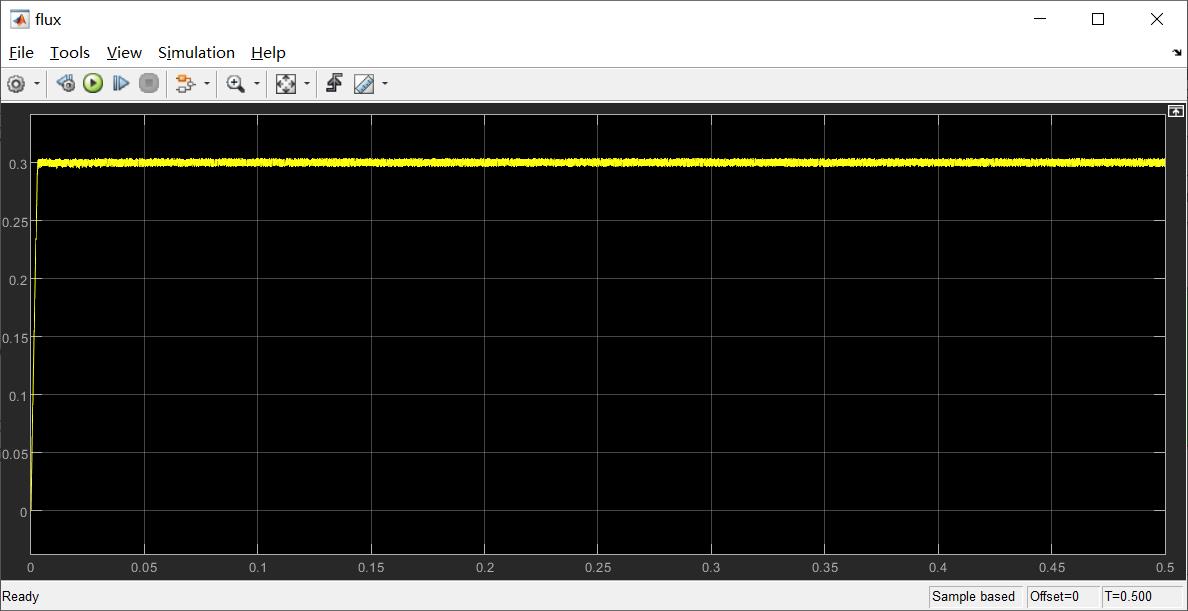
3.2负载工况下
(1)转速响应
转速为阶跃转速,0s由0 r/min阶跃上升至8000 r/min.
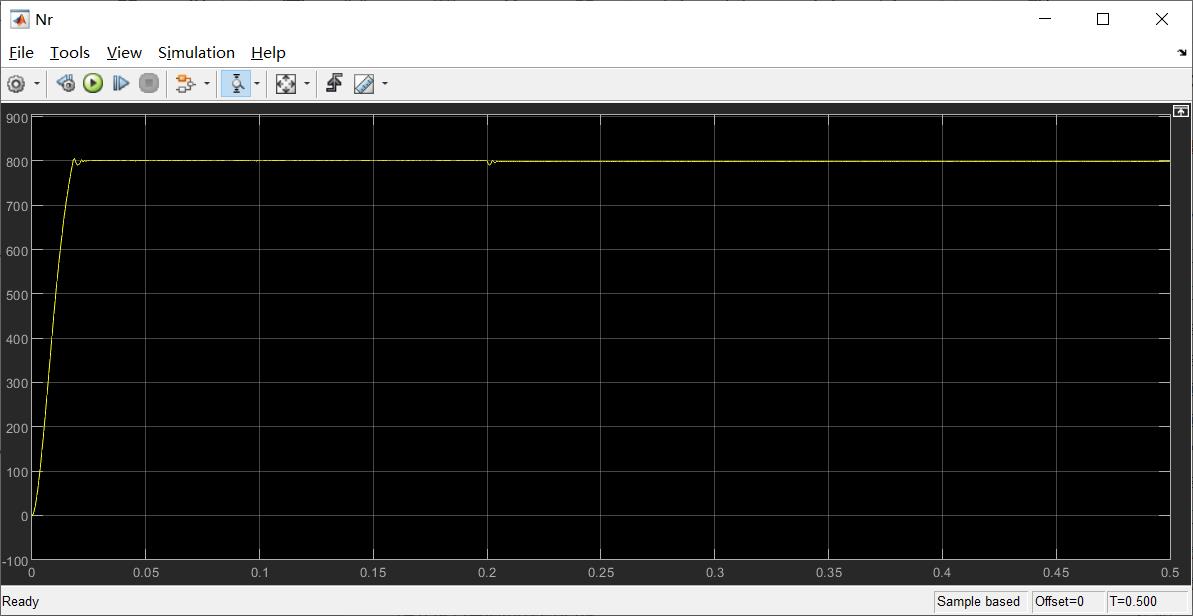
(2)转矩响应
转矩为阶跃负载,0.2s
以上是关于永磁同步电机的直接转矩控制一一一滑模控制器改进DTC的主要内容,如果未能解决你的问题,请参考以下文章