梯度下降法(Gradient Descent)
Posted Debroon
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了梯度下降法(Gradient Descent)相关的知识,希望对你有一定的参考价值。
梯度下降法
梯度下降法,不是一个机器学习算法(既不是再做监督学习,也不是非监督学习,分类、回归问题都解决不了),是一种基于搜索的最优化方法。
梯度下降法作用是,最小化一个损失函数;而如果我们要最大化一个效用函数,应该使用梯度上升法。
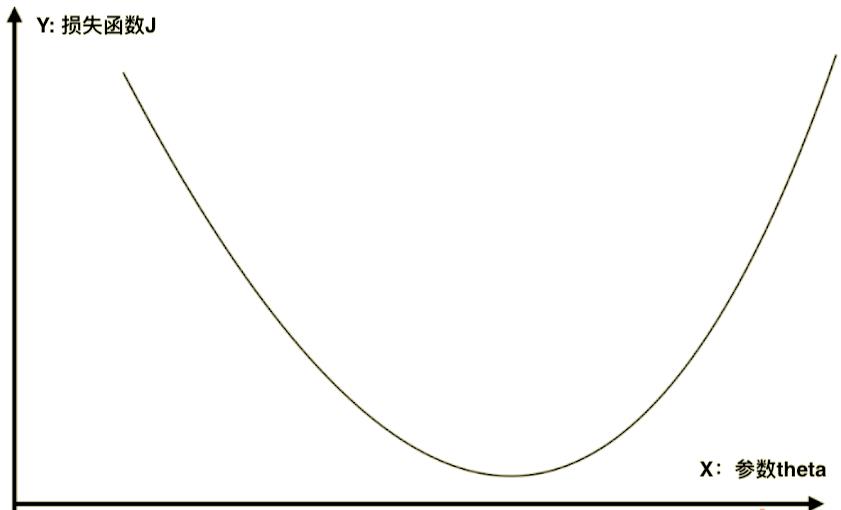
这个二维平面描述了,当我们定义了一个
损
失
函
数
J
损失函数J
损失函数J 后,那么每取一个
参
数
t
h
e
t
a
参数theta
参数theta,
损
失
函
数
J
损失函数J
损失函数J 就会取到一个值。
如下图,对于某一个点,存在一个
参
数
t
h
e
t
a
参数theta
参数theta,相应的就有一个
损
失
函
数
J
损失函数J
损失函数J。

如果蓝点的导数不为零,那么这一点肯定不在一个极值点上
d
J
d
θ
\\frac{dJ}{d\\theta}
dθdJ。
- 在直线方程中,导数代表斜率;
- 在曲线方程中,导数代表切线斜率;
- 在这里,导数代表 θ 单 位 变 化 时 , J 相 应 的 变 化 是 多 少 \\theta单位变化时,J相应的变化是多少 θ单位变化时,J相应的变化是多少。
更进一步,导数(梯度)可以代表方向,对应J增大/减小的方向。
因为我们要寻找的是 损 失 函 数 J 损失函数J 损失函数J 的最小值,那就是负方向: − d J d θ -\\frac{dJ}{d\\theta} −dθdJ。
此外,移动还会有步长: − η d J d θ -\\eta\\frac{dJ}{d\\theta} −ηdθdJ。
移动步长 η \\eta η 是一个常数,通常是 0.1 0.1 0.1,这是一个超参数,需要调参得到最佳 η \\eta η。
整个过程,每次向负方向移动 η \\eta η,再求导数,再移动,不断循环,直到找到最低点。
在我们举的例子里,用的一维函数,直接用导数即可;但在多维函数中,需要对各个方向的分量分别求导,最终得到的方向就是梯度。
梯度下降法的基本思想可以类比为一个下山的过程。假设这样一个场景:
一个人被困在山上,需要从山上下来(找到山的最低点,也就是山谷)。但此时山上的浓雾很大,导致可视度很低。因此,下山的路径就无法确定,他必须利用自己周围的信息去找到下山的路径。这个时候,他就可以利用梯度下降算法来帮助自己下山。具体来说就是,以他当前的所处的位置为基准,寻找这个位置最陡峭的地方,而后朝着山的高度下降的地方走,同理,如果我们的目标是上山,也就是爬到山顶,那么此时应该是朝着最陡峭的方向往上走。而后每走一段距离,都反复采用同一个方法,最后就能成功的抵达山谷。
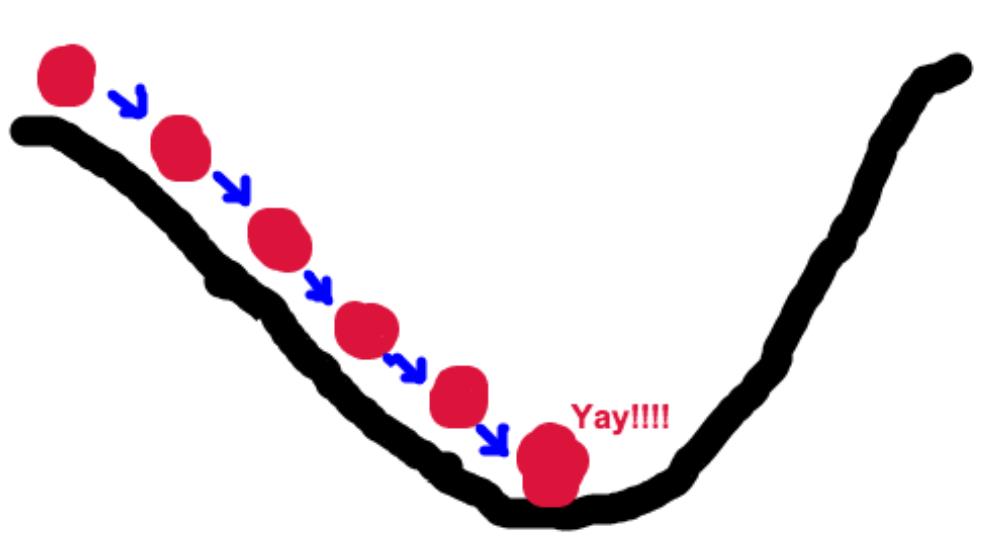
我们同时可以假设这座山最陡峭的地方是无法通过肉眼立马观察出来的,而是需要一个复杂的工具来测量,同时,这个人此时正好拥有测量出最陡峭方向的能力。所以,此人每走一段距离,都需要一段时间来测量所在位置最陡峭的方向,这是比较耗时的。那么为了在太阳下山之前到达山底,就要尽可能的减少测量方向的次数。这是一个两难的选择,如果测量的频繁,可以保证下山的方向是绝对正确的,但又非常耗时,如果测量的过少,又有偏离轨道的风险。所以需要找到一个合适的测量方向的频率,来确保下山的方向不错误,同时又不至于耗时太多!
就是有一个小问题:
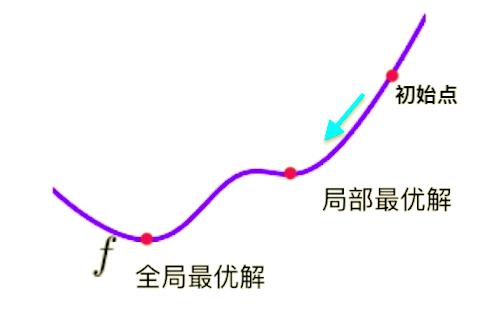
从图中的初始点出发,梯度下降找到的只是局部最优解。
解决方法也很简单:
- 多次运行,随机初始化初始点(初始点也是一个超参数)
假设现在有一张地图,你对这张地图上的地形一无所知,但是如果你报出地图上任何一个位置坐标,系统都能告诉你这个地点的高度是多少。你的任务是在有限的时间内,通过这种问答的试探方法,在地图上找到尽可能高的一座山。你怎么办呢?
最笨的办法是从地图左上角开始一个点一个点的问,可是这样速度太慢了。
-
一个办法是随机地选取若干个点,得到每个点的高度,只要时间还有你就不停地问,时间到了就选择你遇到的最高的一点。这个方法的效率也不行,完全靠运气。
-
还有一个办法是从某一点开始,考察这个点临近一米处各个点的高度,选择最高的一点,而后从这个新点出发,再选择它周围最高的一点。这其实就是一个爬山的办法 —— 这个办法能确保你找到最初一点附近的一座山。
-
而最好的办法,是把随机选点和爬山结合起来。先随机选一些点,找到其中最高的一点,再在这个点附近若干公里的范围内随机选点,又选择其中最高的一点,而后从这点出发爬山。
用这个办法,你未必能发现地图上最高的山,但是一定能在有限的时间内发现一座比较高的山。而如果你一开始的某个点落在了青藏高原上,这个办法可以确保你发现喜马拉雅山。
起始点对梯度下降法是十分重要的,在函数有很多局部最优解的情况下,多次随机选点,也不一定能找到最优解,但一定可以发现更好的解。
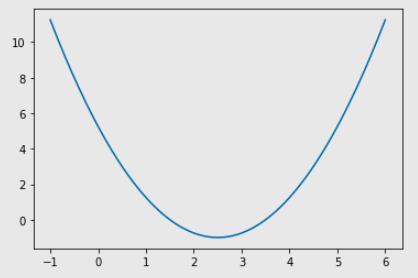
import numpy as np
import matplotlib.pyplot as plt
plot_x = np.linspace(-1, 6, 141)
# 头尾 140 个点
plot_y = (plot_x-2.5)**2-1
# 二次曲线(损失函数),目标找到这条曲线最小值
plt.plot(plot_x, plot_y)
plt.show()
# 求损失函数对应的导数,看当前 theta 对应的导数是多少
def dJ(theta):
return 2*(theta-2.5)
# 求损失函数,看当前 theta 对应的损失函数是多少
def J(theta):
return (theta-2.5)**2-1
# 实现梯度下降法
eta = 0.1
theta = 0.0
epsilon = 1e-8
while 1:
gradient = dJ(theta) # 求梯度(一维函数的梯度就是导数)
last_theta = theta
theta = theta - eta * gradient # 梯度 * (-eta),往负的方向走,步长为 eta
if( abs(J(theta) - J(last_theta)) < epsilon ): # 判断是否是最低点(这一次损失函数比上一次小),浮点数运算有精度问题,不能直接判断
break
print(theta)
print(J(theta), J(last_theta))
输出:
2.499891109642585
-0.99999998814289 -0.9999999814732657
我们可视化一下,这个走法:
# 求损失函数对应的导数,看当前 theta 对应的导数是多少
def dJ(theta):
return 2*(theta-2.5)
# 求损失函数,看当前 theta 对应的损失函数是多少
def J(theta):
return (theta-2.5)**2-1
# 实现梯度下降法
eta = 0.1
theta = 0.0
epsilon = 1e-8
theta_history = [theta]
while 1:
gradient = dJ(theta) # 求梯度(一维函数的梯度就是导数)
last_theta = theta
theta = theta - eta * gradient # 梯度 * (-eta),往负的方向走,步长为 eta
theta_history.append(theta)
if( abs(J(theta) - J(last_theta)) < epsilon ): # 判断是否是最低点(这一次损失函数比上一次小),浮点数运算有精度问题,不能直接判断
break
plt.plot(plot_x, J(plot_x))
plt.plot(np.array(theta_history), J(np.array(theta_history)), color='r', marker='+')
plt.show()
输出:
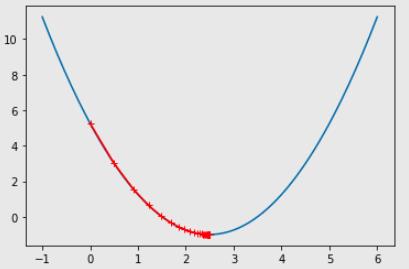
+号是每次的步点,一开始步长大,后面步长就越来越小。虽然公式一直都是乘 eta,而 eta 是不变的常数,但是梯度一开始比较大(比较陡),后面月亮越平缓,步子也就小了。
批量梯度下降法
在上面的文章中,抽出一些多元线性回归的理论推导过程。

-
第一部分:多元线性回归: y = a 1 x 1 + a 2 x 2 + ⋅ ⋅ ⋅ + a n x n + b y=a_{1}x_{1}+a_{2}x_{2}+···+a_{n}x_{n}+b y=a1x1+a2x2+⋅⋅⋅+anxn+b
-
第二部分:为了推导方便,我们构造一个 X 0 i X_{0}^{i} X0i,这个恒等于 1 1 1。
-
第三部分:得到 y ^ = X i ⋅ θ \\hat{y}=X_{i}·\\theta y^=Xi⋅θ。
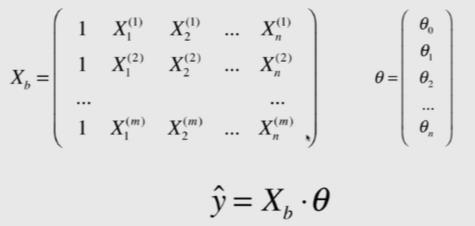
-
第一部分: X b X_{b} Xb 是在 X X X 的基础上,添加了一列 1 ( X 0 i ) 1 (X_{0}^{i}) 1(X0i)。
-
第二部分: y ^ = X i ⋅ θ − > y ^ = X b ⋅ θ \\hat{y}=X_{i}·\\theta~ -> ~\\hat{y}=X_{b}·\\theta y^=Xi⋅θ −> y^=Xb⋅θ
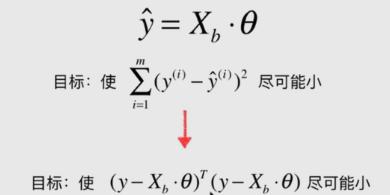
-
第一部分:经过变换,就从原损失函数 ∑ i = 1 m ( y i − y ^ i ) 2 \\sum\\limits_{i=1}^m(y_{i} - \\hat{y}_{i})^{2} i=1∑m(yi−y^i)2中推导出了新损失函数 ∑ i = 1 m ( y − X b ⋅ θ ) T ( y − X b ⋅ θ ) \\sum\\limits_{i=1}^m(y-X_{b}·\\theta)^{T}(y-X_{b}·\\theta) i=1∑m(y−Xb⋅θ)T(y−Xb⋅θ)。
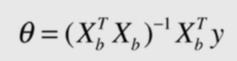
-
第一部分:推导出来的结果,也称为多元线性回归的正规方程解。
好,看看线性回归里面的梯度下降法。
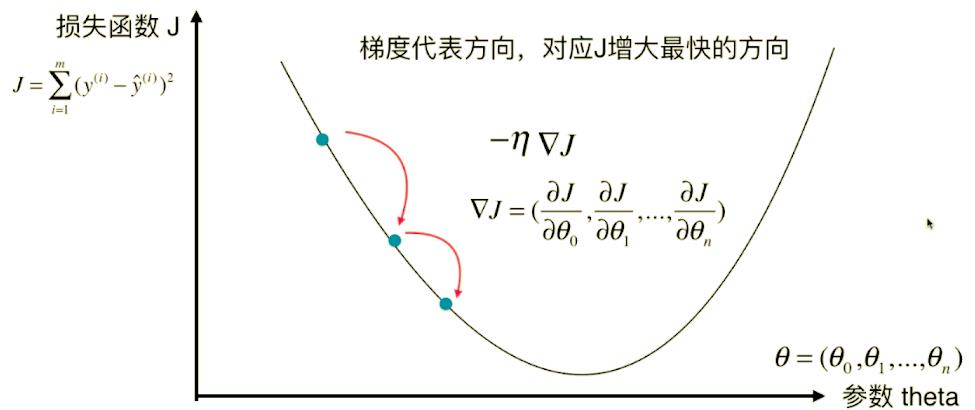
-
梯度下降的Y轴:多元线性回归的损失函数: J = ∑ i = 1 m ( y i − y ^ i ) 2 J = \\sum\\limits_{i=1}^m(y_{i} - \\hat{y}_{i})^{2} J=i=1∑m(yi−y^i)2。
-
梯度下降的X轴:参数 θ \\theta