Transformation HDU - 4578

Posted 2021-06-19 Jozky86

Transformation HDU - 4578

题意：

选定一段连续区间[l,r],有三种操作：
操作1：对区间内值+c
操作2：对区间内值*c
操作3：将区间内的值都改为c
操作4：查询区间内每个数p次方的和
p=1，2，3

题解:

参考题解
加强版线段树，对于本题需要三个标记，add的加法标记，mul的乘法标记，alt的修改标记，因为p=1，2，3，所以我们用sum1，sum2，sum3分别表示一次方和，平方和，立方和
然后我们要确定标记的优先级，alt第一，mul第二，add第三，pushdown要按照这样的顺序下压标记
当传来add标记时，更新自身时，要注意计算sum3，sum2，sum1的先后顺序，因为sum3的计算需要sum2和sum1，sum2的计算需要sum1
这三个sum的计算方法：

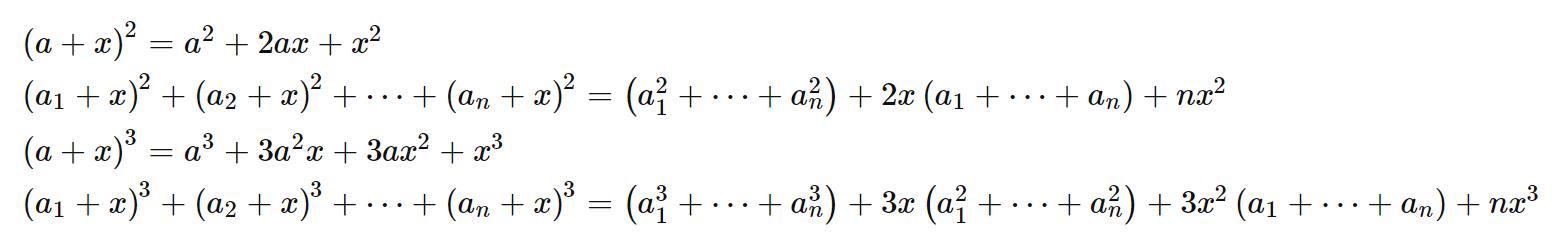
sum3 = ( sum3%MOD + 3*x%MOD*sum2%MOD + 3*x%MOD*x%MOD*sum1%MOD + (r-l+1)*x%MOD*x%MOD*x%MOD ) % MOD;
sum2 = ( sum2%MOD + 2*x%MOD*sum1%MOD + (r-l+1)%MOD*x%MOD*x%MOD ) % MOD;
sum1 = ( sum1%MOD + (r-l+1)%MOD*x%MOD ) % MOD;

代码:

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int maxn=100000+10;
const int MOD=10007;

int n,m;

/********************************* Segment Tree - st *********************************/
struct Node
{
    int l,r;
    int sum1,sum2,sum3;
    int add,mul,alt;
    void Update_Alt(int x)
    {
        x%=MOD;
        sum1 = (r-l+1) * x % MOD;
        sum2 = (r-l+1) * x % MOD * x % MOD;
        sum3 = (r-l+1) * x % MOD * x % MOD * x % MOD;
        alt=x;
        add=0;
        mul=1;
    }
    void Update_Mul(int x)
    {
        x%=MOD;
        sum1 = sum1 % MOD * x % MOD;
        sum2 = sum2 % MOD * x % MOD * x % MOD;
        sum3 = sum3 % MOD * x % MOD * x % MOD * x % MOD;
        mul = mul % MOD * x % MOD;
        add = add % MOD * x % MOD;
    }
    void Update_Add(int x)
    {
        x%=MOD;
        sum3 = ( sum3%MOD + 3*x%MOD*sum2%MOD + 3*x%MOD*x%MOD*sum1%MOD + (r-l+1)*x%MOD*x%MOD*x%MOD ) % MOD;
        sum2 = ( sum2%MOD + 2*x%MOD*sum1%MOD + (r-l+1)%MOD*x%MOD*x%MOD ) % MOD;
        sum1 = ( sum1%MOD + (r-l+1)%MOD*x%MOD ) % MOD;
        add=(add%MOD+x)%MOD;
    }
}node[4*maxn];
void Pushdown(int root)
{
    int ls=root*2, rs=root*2+1;
    if(node[root].alt!=0)
    {
        node[ls].Update_Alt(node[root].alt);
        node[rs].Update_Alt(node[root].alt);
        node[root].alt=0;
    }
    if(node[root].mul!=1)
    {
        node[ls].Update_Mul(node[root].mul);
        node[rs].Update_Mul(node[root].mul);
        node[root].mul=1;
    }
    if(node[root].add!=0)
    {
        node[ls].Update_Add(node[root].add);
        node[rs].Update_Add(node[root].add);
        node[root].add=0;
    }
}
void Pushup(int root)
{
    int ls=root*2, rs=root*2+1;
    node[root].sum1=(node[ls].sum1+node[rs].sum1)%MOD;
    node[root].sum2=(node[ls].sum2+node[rs].sum2)%MOD;
    node[root].sum3=(node[ls].sum3+node[rs].sum3)%MOD;
}
void Build(int root,int l,int r) //对区间[l,r]建树
{
    if(l>r) return;
    node[root].l=l; node[root].r=r;
    node[root].sum1=0;
    node[root].sum2=0;
    node[root].sum3=0;
    node[root].alt=0;
    node[root].add=0;
    node[root].mul=1;

    if(l<r)
    {
        int mid=l+(r-l)/2;
        Build(root*2,l,mid);
        Build(root*2+1,mid+1,r);
        Pushup(root);
    }
}
void Alt(int root,int st,int ed,ll val) //区间[st,ed]全部改成val
{
    if(st>node[root].r || ed<node[root].l) return;0-9【‘- 
    if(st<=node[root].l && node[root].r<=ed) node[root].Update_Alt(val);
    else
    {
        Pushdown(root);
        Alt(root*2,st,ed,val);
        Alt(root*2+1,st,ed,val);
        Pushup(root);
    }
}
void Mul(int root,int st,int ed,ll val) //区间[st,ed]全部乘val
{
    if(st>node[root].r || ed<node[root].l) return;
    if(st<=node[root].l && node[root].r<=ed) node[root].Update_Mul(val);
    else
    {
        Pushdown(root);
        Mul(root*2,st,ed,val);
        Mul(root*2+1,st,ed,val);
        Pushup(root);
    }
}
void Add(int root,int st,int ed,ll val) //区间[st,ed]全部加上val
{
    if(st>node[root].r || ed<node[root].l) return;
    if(st<=node[root].l && node[root].r<=ed) node[root].Update_Add(val);
    else
    {
        Pushdown(root);
        Add(root*2,st,ed,val);
        Add(root*2+1,st,ed,val);
        Pushup(root);
    }
}
int Query(int root,int st,int ed,int p) //查询区间[st,ed]的p次方和
{
    if(st>node[root].r || ed<node[root].l) return 0;
    if(st<=node[root].l && node[root].r<=ed)
    {
        if(p==1) return node[root].sum1;
        if(p==2) return node[root].sum2;
        if(p==3) return node[root].sum3;
    }
    else
    {
        Pushdown(root);
        int ls=Query(root*2,st,ed,p)%MOD;
        int rs=Query(root*2+1,st,ed,p)%MOD;
        Pushup(root);
        return (ls+rs)%MOD;
    }
}
/********************************* Segment Tree - st *********************************/

int main()
{
    while(scanf("%d%d",&n,&m) && n*m!=0)
    {
        Build(1,1,n);
        for(int i=1;i<=m;i++)
        {
            int op; scanf("%d",&op);
            if(op==1)
            {
                int x,y,k;
                scanf("%d%d%d",&x,&y,&k);
                Add(1,x,y,k);
            }
            if(op==2)
            {
                int x,y,k;
                scanf("%d%d%d",&x,&y,&k);
                Mul(1,x,y,k);
            }
            if(op==3)
            {
                int x,y,k;
                scanf("%d%d%d",&x,&y,&k);
                Alt(1,x,y,k);
            }
            if(op==4)
            {
                int l,r,p;
                scanf("%d%d%d",&l,&r,&p);
                printf("%d\\n",Query(1,l,r,p));
            }
        }
    }
}