已知二叉树先序遍历和后序遍历序列，求可能的中序遍历序列及方案数

Posted 2021-06-19 牧空

分析

参考
理论依据在参考中,这里简单说明一下
$$\begin{gathered} 假设先序遍历序列为Pre,后序遍历的序列为Post \\ 记其中一个结点为v,则在Pre中存在以v为开头的最长后缀P_v \\ 使得在Post中有以v为结尾的最长前缀S_v与P_v中元素相同 \end{gathered}$$
对于树

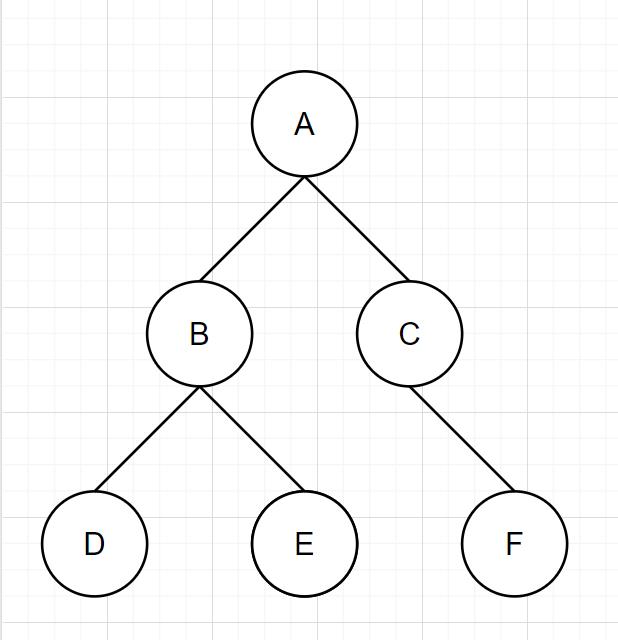
先序为ABDECF
后序为DEBFCA
以C为例，对于先序C之后不会出现B来干扰，所以不会$P_v$和$S_v$不会将兄弟结点加进来
$$\begin{gathered} 已经获取了P_v和S_v,如果P_v的第一个元素等于S_v的倒数第一个元素 \\ 说明v只有一个子树,那么类型数量就要翻倍 \end{gathered}$$

代码

#include <iostream>
#include <cstdio>
#include <string>
using namespace std;

int main(int argc, char const *argv[])
{
    string pre, post;
    cin >> pre >> post;
    int i = 0, sum = 1;
    while (i < pre.length() - 1)
    {
        int j = post.find(pre[i], 0);
        if (pre[i + 1] == post[j - 1])
            sum *= 2;
        i++;
    }
    printf("%d\\n", sum);
    return 0;
}

---

有错误望指正