文献阅读08期：SBM-DEA混合蒙特卡洛的能用效用评估

Posted 2021-06-18 RaZLeon

[ 文献阅读·能源 ] Energy supply efficiency evaluation of integrated energy systems using novel SBM-DEA integrating Monte Carlo [1]

推荐理由： 以往的DEA模型分为两种，径向模型和角度量模型，这两种模型要么没有考虑松弛问题，要么仅考虑单一的输入输出。本文提出的MC-SBM-DEA可以说是兼顾了两个方面，值得借鉴

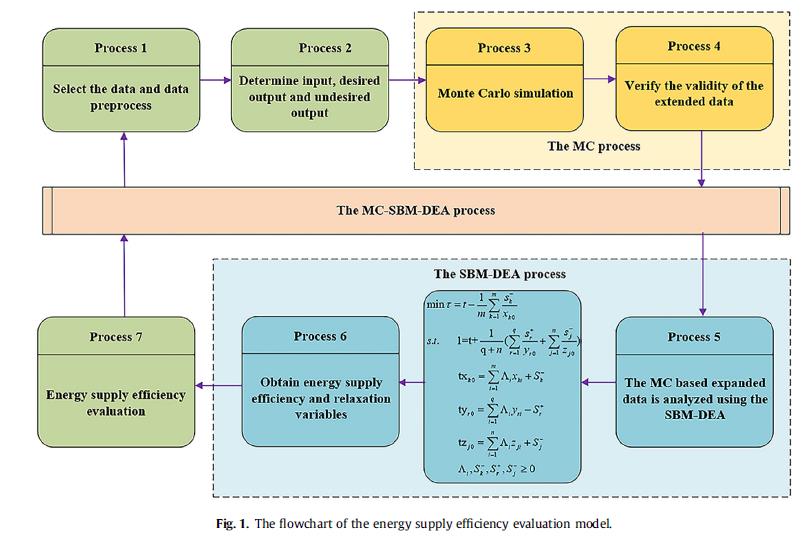
1.摘要&简介

• 主流的DEA模型分为两种，径向模型和角度量模型。径向模型经常忽视松弛问题，而角度量模型进考虑单一的输入输出。
• SBM-DEA模型同时兼顾了两个方面且有以下重要特性：
  1. 效率的度量不受决策单元的影响（decision-making units）
  2. 效率值和输入输出之差是单调递减的。

2.问题模型

2.1. SBM-DEA模型

• 若有m个输入n个出，所有可能集合可定义为：
  P = { ( x , y ) ∣ x ≥ X λ , y ≤ Y λ , λ ≥ 0 } (1) P=\\{(x, y) \\mid x \\geq X \\lambda, y \\leq Y \\lambda, \\lambda \\geq 0\\}\\tag{1} P={(x,y)∣x≥Xλ,y≤Yλ,λ≥0}(1)
• 其中$x$是输入，$y$是输出，$\lambda$为调整矩阵。
• 通过测量$\mathrm{DMU}\left(x_0,y_0\right)$的效率，SBM-DEA模型的基础形式可以写为以下形式：
  $$\begin{array}{l}{\rho }^{\ast }=\min \frac{1-\frac{1}{m}{\sum }_{k=1}^m\frac{s_k^{-}}{x_{k0}}}{1-\frac{1}{n}{\sum }_{r=1}^n\frac{s_r^{+}}{y_{r0}}}\\ \text{ S.t. }{\mathrm{x}}_0=X\lambda +s^{-}\\ {\mathrm{y}}_0=Y\lambda -s^{+}\\ \lambda \ge 0,s^{-}\ge 0,s^{+}\ge 0\end{array}\text{\hspace{1em}(2)}$$
  其中，${\rho }^{\ast }$代表$\mathrm{DMU}\left(x_0,y_0\right)$的效率值，$X_{r0}$和$Y_{r0}$为第j个DMU的输入输出向量。${\mathrm{s}}^{+}$和${\mathrm{s}}^{-}$为输入输出相对应的松弛变量。$s_k^{-}$代表第k个输入的冗余，$s_r^{+}$代表第r个输出的不足。
• 目标函数上下分别代表输入输出的效率水平，任何一方变化都会造成效率值的变化。
• 将标量t引入式2有：
  $$\begin{array}{l}\min \tau =t-\frac{1}{m}{\sum }_{k=1}^m\frac{t{s}_k^{-}}{x_{k0}}\\ \text{ s.t. }1=\mathrm{t}+\frac{1}{\mathrm{n}}{\sum }_{r=1}^n\frac{t{s}_r^{+}}{y_{r0}}\\ {\mathrm{x}}_0=X\lambda +s^{-}\\ {\mathrm{y}}_0=Y\lambda -s^{+}\\ \lambda \ge 0,s^{-}\ge 0,s^{+}\ge 0,\mathrm{t}>0\end{array}$$