Groth16 学习笔记
Posted mutourend
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了Groth16 学习笔记相关的知识,希望对你有一定的参考价值。
1. 引言
Groth 2016年论文《On the Size of Pairing-based Non-interactive Arguments》。
相关代码实现有:
- https://github.com/matter-labs/bellman
- https://github.com/zkcrypto/bellman
- https://github.com/arkworks-rs/groth16
非交互式argument 允许Prover convince Verifier that a statement is true。
近期在理论和实践上,构建具有small size和low verification complexity的高效非交互式argument均取得重大进展,具有small size和low verification complexity的非交互式argument也称为SNARGs (succinct non-interactive arguments) 或 SNARKs (succinct non-interactive arguments of knowledge)。
很多SNARGs都是基于pairing 构建的,这种构建方式:
- proof中包含多个group elements
- verification中需验证多个pairing product方程式
1.1 相关研究
Goldwasser等人在1989年论文[GMR89]中指出,零知识证明应具有如下属性:
- Completeness完备性:已知statement和相应的witness,Prover可convince Verifier。
- Soundness 可靠性:malicious Prover无法convince Verifier of a false statement。
- Zero-knowledge 零知识性:proof除了说明the truth of the statement,不会泄露任何其它信息,尤其是Prover的witness。
Blum等人在[FBM88]中将以上观点扩展至 non-interactive zero-knowledge (NIZK) proofs in the common reference string model。NIZK proofs可用于构建non-interactive cryptographic schemes,如数字签名和CCA-secure public key encryption。
零知识证明中的communication cost是一个重要的性能指标。Kilian在[Kil92]中提出了第一个sublinear communication cost的方案,其发送的bits数量比 待证明的statement size要小。Micali [Mic00]和Kilian [Kil95]中指出,Prover可利用a cryptographic function来计算Verifier的challenges,从而实现public coin和zero-knowledge。
Groth, Ostrovsky和Sahai [GOS12,GOS06,Gro06,GS12]中介绍了pairing-based NIZK proofs,产生了第一个基于standard assumption的linear size proof。[Gro10]中将这些技术与[Gro09]中的interactive zero-knowledge argument结合,提出了第一个constant size NIZK argument。[Lip12]中基于progression-free sets减少了common reference string的size。
[Gro10]中的constant size NIZK argument中构建了一系列的polynomial方程式,使用pairings来高效验证这些方程式。Gennaro [GGPR13] 中富有见解的采用基于Lagrange interpolation polynomials来构建polynomial 方程式,从而实现了pairing-based NIZK argument,其common reference string size与statement size和witness size呈正比。在[GGPR13]中给出了2种类型的方程式:
- Quadratic span programs for proving Boolean circuit satisfiability
- Quadratic arithmetic programs for proving arithmetic circuit satisfiability
Lipmaa [Lip13] 建议使用error correcting codes来构建更高效的quadratic span programs。
Danezis等人 [DFGK14]中优化quadratic span program为square span program,使得boolean circuit satisfiability的proof中仅包含4个group elements。
当前一些研究在理论上也取得了进展,如:
[PHGR13,BCG+13,BFR+13,BCTV14b,KPP+14,BBFR15,CTV15,WSR+15,CFH+15,SVdV16]
大多数高效实现都是将[GGPR13]中改进的quadratic arithmetic program 与 可生成合适quadratic arithmetic program的compiler 结合。如libsnark [BCTV14b, BSCG+14]中也包含基于[DFGK14]中的NIZK argument。
非交互式argument可用于:
- Verifiable computation:如算力外包等。零知识SNARKs是Pinocchio coin [DFKP13] 和 Zerocash [BCG+14]的核心元素。
1.2 本文主要贡献
本文的主要贡献有:
(1)succinct NIZK
为arithmetic circuit satisfiability构建了pairing-based (preprocessing) SNARK。采用非对称pairing,proof中仅包含3个group element,verification中仅需验证一个paring product方程式,该方程式中一共只有3个pairing计算。
本文的构建方式支持任意类型的pairings,包括Type III pairings,Type III pairings为当前效率最高的pairings。
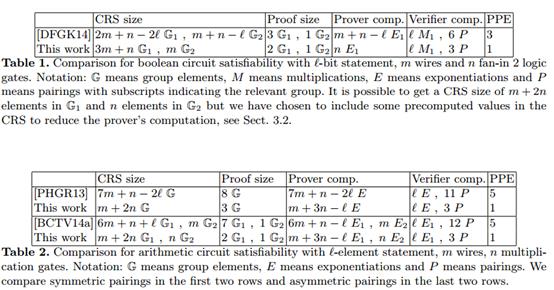
对boolean circuit satisfiability和arithmetic circuit satisfiability的性能对比如下图所示:【评估的维度有:common reference string (CRS)的size、proof size、Prover的computation、Verifier的computation、验证proof所需的pairing product equations的数量。】
(2)lower bounds
回答了Bitansky等人(TCC2013)的开放问题,说明2-move linear interactive proofs cannot have a linear decision procedure。对于使用generic asymmetric bilinear group的SNARGs,prover和verifier的group operation操作中不可能仅包含一个group element。这给出了pairing-based SNARGs的下限值。至于是否能在现有3个group elements的基础上进一步优化proof size为2个group elements,目前仍是一个开放问题。
1.3 Bilinear groups
bilinear groups ( p , G 1 , G 2 , G T , e , g , h ) (p,\\mathbb{G}_1,\\mathbb{G}_2,\\mathbb{G}_T,e,g,h) (p,G1,G2,GT,e,g,h) 具有如下属性:
- G 1 , G 2 , G T \\mathbb{G}_1,\\mathbb{G}_2,\\mathbb{G}_T G1,G2,GT 为groups of prime order p p p
- pairing e : G 1 × G 2 → G T e:\\mathbb{G}_1\\times \\mathbb{G}_2\\rightarrow \\mathbb{G}_T e:G1×G2→GT 为bilinear map
- g g g为generator for G 1 \\mathbb{G}_1 G1, h h h为generator for G 2 \\mathbb{G}_2 G2, e ( g , h ) e(g,h) e(g,h)为generator for G T \\mathbb{G}_T GT。
- 存在高效的算法来计算group operations、evaluate bilinear map、decide membership of the groups、decide equality of group elements以及sample generators of the groups。将这些计算统称为generic group operations。
基于的安全假设为DLP。
做了如下约定:
- [ a ] 1 [a]_1 [a]1表示 g a g^a ga, [ b ] 2 [b]_2 [b]2表示 h b h^b hb, [ c ] T [c]_T [c]T表示 e ( g , h ) c e(g,h)^c e(g,h)c。
- g = [ 1 ] 1 , h = [ 1 ] 2 , e ( g , h ) = [ 1 ] T g=[1]_1,h=[1]_2,e(g,h)=[1]_T g=[1]1,h=[1]2,e(g,h)=[1]T
- [ a ] T + [ b ] T = [ a + b ] T [a]_T+[b]_T=[a+b]_T [a]T+[b]T=[a+b]T
- [ a ⃗ ] i + [ b ⃗ ] i = [ a ⃗ + b ⃗ ] i [\\vec{a}]_i+[\\vec{b}]_i=[\\vec{a}+\\vec{b}]_i [a]i+[b]i=[a+b]i为a vector of group elements
1.4 non-interactive zero-knowledge arguments of knowledge
relation
(
ϕ
,
w
)
∈
R
(\\phi,w)\\in R
(ϕ,w)∈R,其中
ϕ
\\phi
ϕ为statement,
w
w
w为witness。
publicly verifiable non-interactive argument包含了4个probabilistic polynomial algorithms
(
S
e
t
u
p
,
P
r
o
v
e
,
V
f
y
,
S
i
m
)
(Setup, Prove, Vfy, Sim)
(Setup,Prove,Vfy,Sim):
- ( σ , τ ) ← S e t u p ( R ) (\\sigma,\\tau)\\leftarrow Setup(R) (σ,τ)←Setup(R):setup算法,输入为relation R R R,输出为common reference string σ \\sigma σ和相应的simulation trapdoor τ \\tau τ。
- π ← P r o v e ( R , σ , ϕ , w ) \\pi\\leftarrow Prove(R,\\sigma,\\phi,w) π←Prove(R,σ,ϕ,w):Prover算法,输入为common reference string σ \\sigma σ、 ( ϕ , w ) ∈ R (\\phi,w)\\in R (ϕ,w)∈R,输出为argument π \\pi π。
- 0 / 1 ← V f y ( R , σ , ϕ , π ) 0/1\\leftarrow Vfy(R,\\sigma,\\phi,\\pi) 0/1←Vfy(R,σ,ϕ,π):Verification算法,输入为common reference string σ \\sigma σ、statement ϕ \\phi ϕ、argument π \\pi π,输出为0(reject) 或 1(accept)。
- π ← S i m ( R , τ , ϕ ) \\pi\\leftarrow Sim(R,\\tau,\\phi) π←Sim(R,τ,ϕ):Simulator算法,输入为simulation trapdoor τ \\tau τ、statement ϕ \\phi ϕ,输出为argument π \\pi π。
可将common reference σ \\sigma σ分为两部分:
- σ P \\sigma_P σP,给Prover用
- σ V \\sigma_V σV,给Veriifier用
若 σ V \\sigma_V σV可根据 σ P \\sigma_P σP推导获得,则可称为public verifiable non-interactive argument
以上是关于Groth16 学习笔记的主要内容,如果未能解决你的问题,请参考以下文章