leetcode 面试题 08.12. 八皇后----回溯篇7

Posted 2021-06-18 大忽悠爱忽悠

八皇后题解集合

• 回溯法
• 判断当前位置是否能放置皇后的另一种思路
• 总结

---

回溯法

之前已经写过了一篇文章关于八皇后问题，本题旧题重拾，详细讲解一番

八皇后问题轻松解决

注意:

皇后的走法是：可以横直斜走，格数不限。因此要求皇后彼此之间不能相互攻击，等价于要求任何两个皇后都不能在同一行、同一列以及同一条斜线上。

并且本题相对原题做了扩展，求的是N皇后的各种摆法

思路：

问题分析：

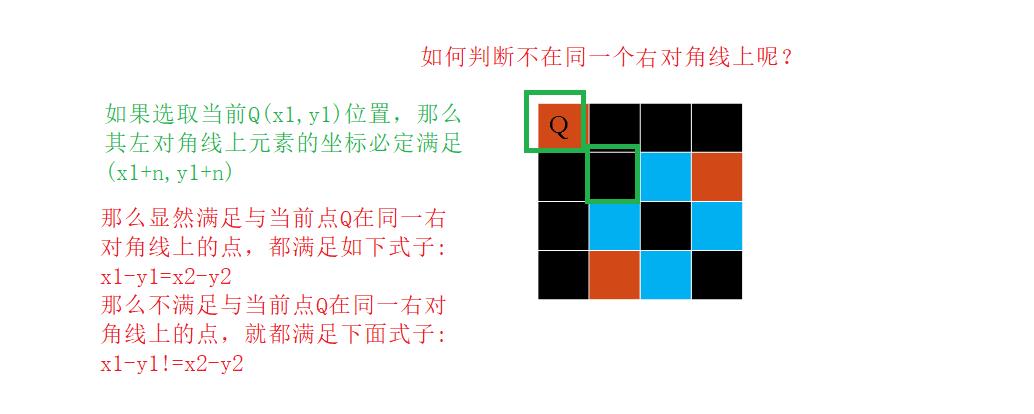
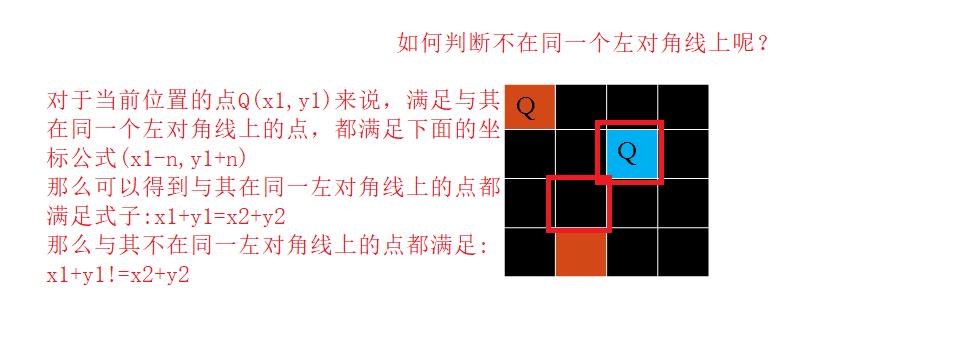
• 假设有皇后Q1(x1,y1)和Q2(x2,y2)
• 不在同一行：x1!=x2
• 不在同一列：y1!=y2
• 不在同一左对角线上：x1+ y1 != x2 +y2
• 不在同一右对角线上：x1-y1 !=x2-y2
• 不在同一左对角线上和不在同一右对角线上上的两个条件可以合并为: abs(x1-x2) != abs(y1-y2)

解释如何判断不在同一个对角线上面:


回溯法思路:

尽量把问题树形化，这道题我们可以把对每个皇后位置的寻找，变成对多叉树的遍历过程

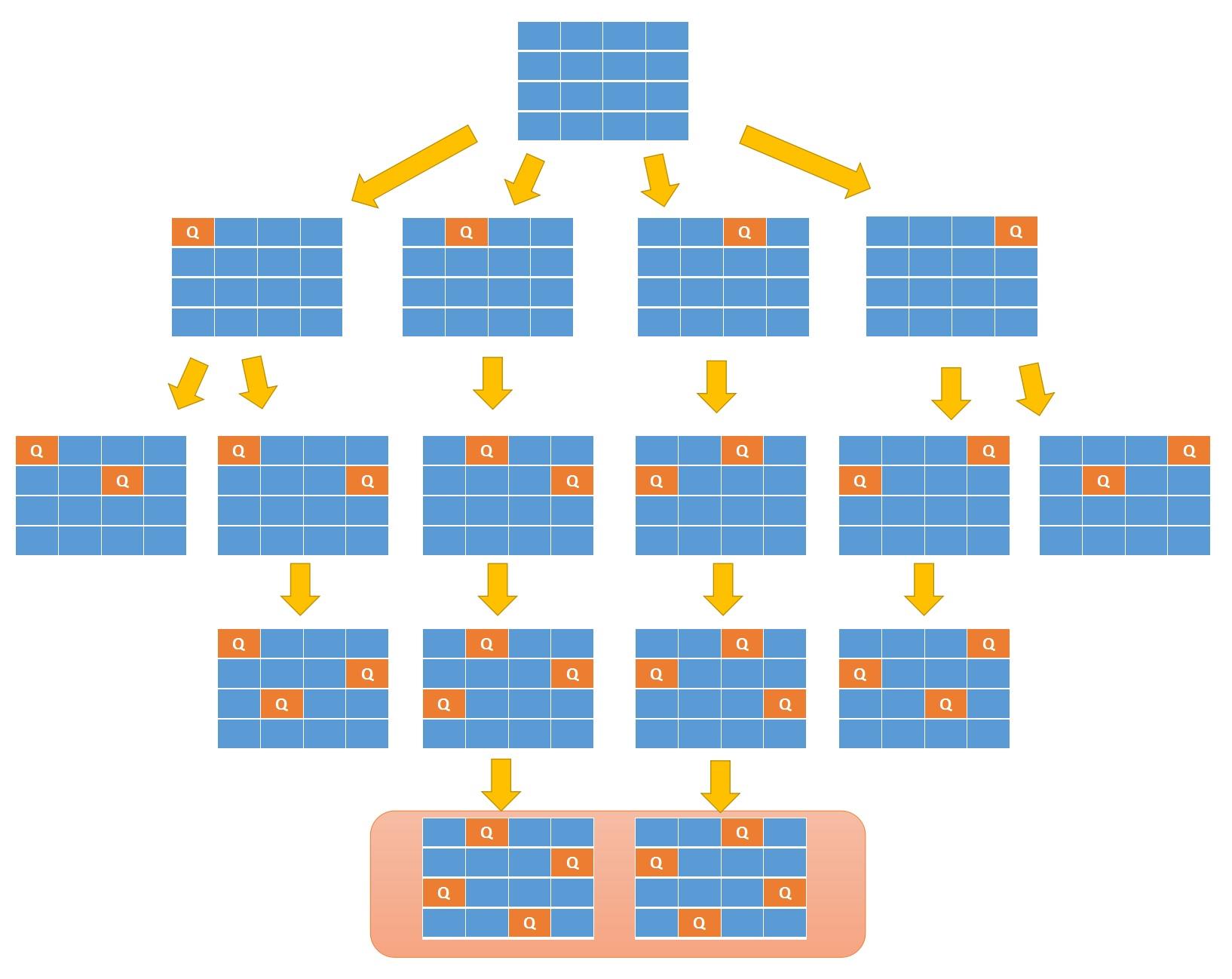
从图中，可以看出，二维矩阵中矩阵的高就是这颗树的高度，矩阵的宽就是树形结构中每一个节点的宽度。

那么我们用皇后们的约束条件，来回溯搜索这颗树，只要搜索到了树的叶子节点，说明就找到了皇后们的合理位置了。

下面先来看一下回溯模板

void backtracking(参数) {
    if (终止条件) {
        存放结果;
        return;
    }
    for (选择：本层集合中元素（树中节点孩子的数量就是集合的大小）) {
        处理节点;
        backtracking(路径，选择列表); // 递归
        回溯，撤销处理结果
    }
}

对于本题而言:

• 递归函数参数:

二维数组ret来记录最终结果。参数n是二维矩阵的大小，然后用row来记录当前遍历到棋盘的第几层了。

代码如下:

vector<vector<string>> result;
void backtracking(int n, int row, vector<string>& chessboard) 
{
}

• 递归终止条件

在如下树形结构中：

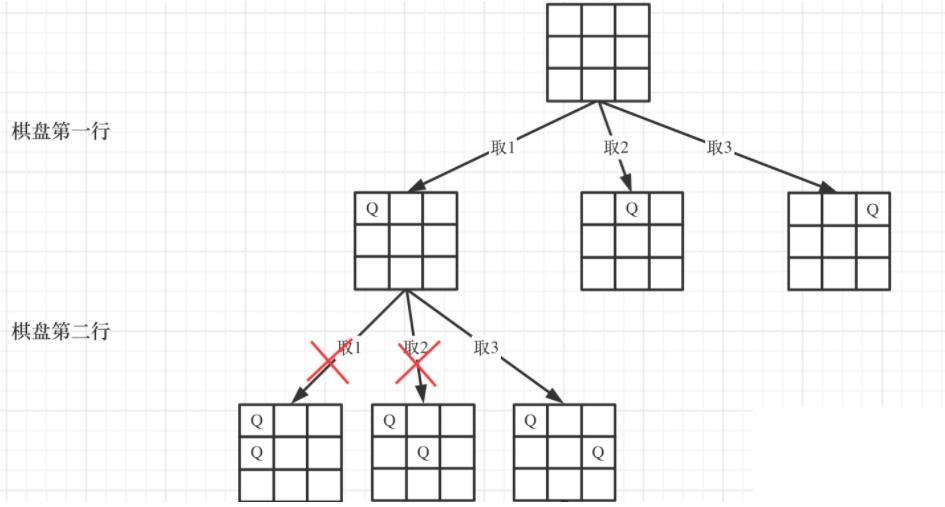
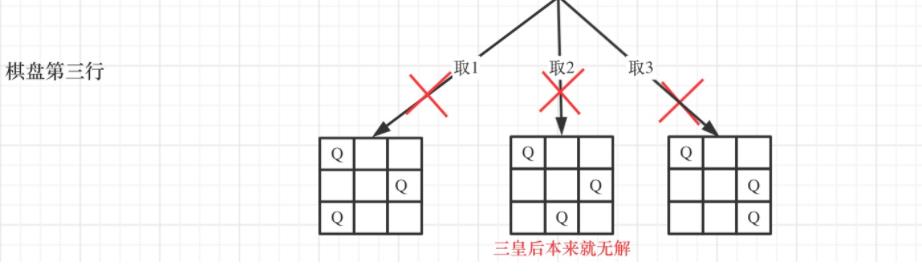
可以看出，当递归到棋盘最底层（也就是叶子节点）的时候，就可以收集结果并返回了。

代码如下:

if (row == n) {
    result.push_back(chessboard);
    return;
}

• 单层搜索的逻辑

递归深度就是row控制棋盘的行，每一层里for循环的col控制棋盘的列，一行一列，确定了放置皇后的位置。

每次都是要从新的一行的起始位置开始搜，所以都是从0开始。

代码如下：

for (int col = 0; col < n; col++) {
    if (isValid(row, col, chessboard, n)) { // 验证合法就可以放
        chessboard[row][col] = 'Q'; // 放置皇后
        backtracking(n, row + 1, chessboard);
        chessboard[row][col] = '.'; // 回溯，撤销皇后
    }
}

• 验证当前皇后放置的是否合法

按照如下标准去重：

• 不能同行
• 不能同列
• 不能同斜线 （45度和135度角）

代码如下:

bool isValid(int row, int col, vector<string>& chessboard, int n) {
    int count = 0;
    // 检查列
    for (int i = 0; i < row; i++) { // 这是一个剪枝
        if (chessboard[i][col] == 'Q') {
            return false;
        }
    }
    // 检查 45度角是否有皇后
    for (int i = row - 1, j = col - 1; i >=0 && j >= 0; i--, j--) {
        if (chessboard[i][j] == 'Q') {
            return false;
        }
    }
    // 检查 135度角是否有皇后
    for(int i = row - 1, j = col + 1; i >= 0 && j < n; i--, j++) {
        if (chessboard[i][j] == 'Q') {
            return false;
        }
    }
    return true;
}

上面判断合法的代码还可以简化：

为什么可以写成这样，参考:轻松解决八皇后

//判断第n个皇后与之前i个皇后位置是否冲突
bool judge(vector<int>& a,int n)
{
	for (int i = 0; i < n; i++)
	{
		if (a[n] != a[i] && abs(a[n] - a[i]) == abs(n - i))
			return true;
	}
	return false;
}

完整回溯法代码:

class Solution {
	vector<vector<string>> ret;//保存所有可行的八皇后放置方案结果
	vector<string> ans;//保存当前可行的八皇后放置方案
	vector<int> a; //用一个一维数组a来表示每个皇后的位置，a[2] = 4表示皇后的位置位于a(2, 4), 即二行四列上
public:
	vector<vector<string>> solveNQueens(int n)
	{
		ans.resize(n, string(n,'.'));
		backTrace(0, n);
		return ret;
	}
	void backTrace(int n, int N)
	{
		if (n == N)//最后一个皇后放置完毕
			ret.push_back(ans);
		else
		{
			//对每一列进行试探
			for (int i = 0; i<N; i++)
			{
				//将当前皇后放置在第n行，第i列上
				a.push_back(i);
				ans[n][i] = 'Q';
				//如果当前n行i列能够放置皇后，那么就继续寻找下一个皇后的合适放置位置
				if(isValild(n))
				backTrace(n + 1, N);
				//如果找到了一种解，或者当前状态无解，那么恢复到上一层的状态，去寻找其他可能解
				a.pop_back();
				ans[n][i] = '.';
			}
		}
	}
	bool isValild(int n)//这里n是正在放置第几个皇后，也可以理解为正在第几行放置皇后
	{
		//第n行要放置的皇后需要和前面n-1行已经放置的皇后进行检查，看是否产生位置冲突
		for (int i = 0; i <n; i++)
		{
			if (a[n] == a[i] || abs(a[n] - a[i]) == abs(n - i))
				return false;
		}
		return true;
	}
};

---

判断当前位置是否能放置皇后的另一种思路

改用三个集合来判断，一个代表竖着的一列，一个代表左斜线，一个代表右斜线。

竖着的一列好办，只要判断坐标[x,y]中的y是否在集合中就可以了，如果存在表示竖着的这一列曾经摆放过皇后。

我们看下如何处理左边那条斜线(左上到右下)如下图：

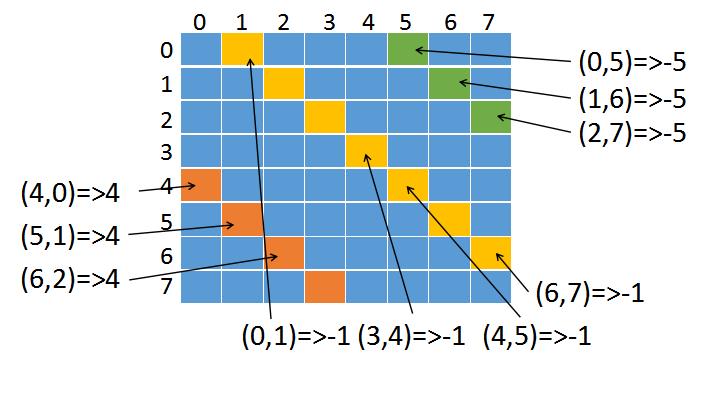
左上到右下的斜线有一个规律，同一条斜线上，x-y得到的值都是相等的

橙色斜线上的四个坐标减出的值都是一样的，同理黄色、绿色也是。

我们只要判断x-y是否在左斜线集合中就可以判断出左斜线上是否有皇后。

右边那条斜线(左下到右上)如下图：

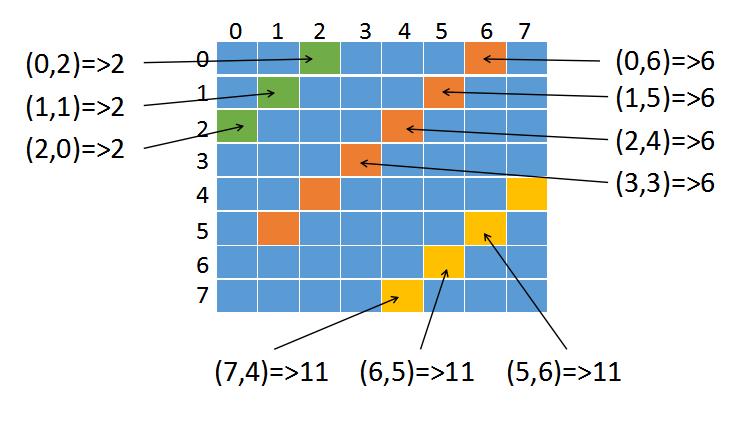
同样也有一个规律，在同一样斜线上，x+y的值是相等的

橙色斜线上的六个坐标加出的值都是一样的，同理黄色、绿色也是。

我们只要判断x+y是否在右斜线集合中就可以判断出右斜线上是否有皇后。

这里我们用一个N行的数组，数组下标i就对应原先N * N数组中第i行的皇后位置。

即a[0]=3，表示第0行,第3列放置了一个皇后

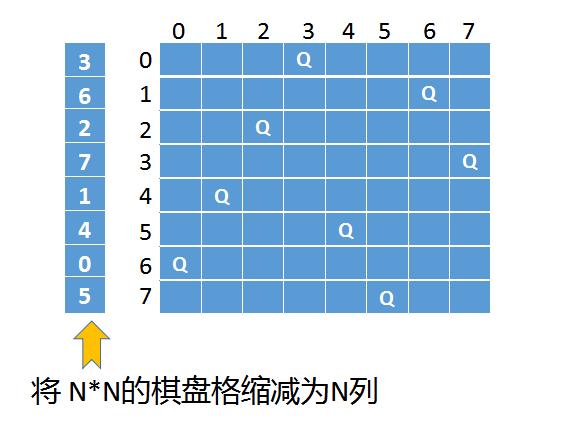
这里可以用三个set集合，用来判断保存已经放置过的皇后的位置,当然也可以改用三个一维数组来进行已经放置过的标记

使用三个set集合的代码:

class Solution {
	vector<vector<string>> ret;//保存所有可行的八皇后放置方案结果
	vector<string> ans;//保存当前可行的八皇后放置方案
	unordered_set<int> col;//判断列
	unordered_set<int> leftSlope;//判断左对角线---x-y
	unordered_set<int> rightSlope;//判断右对角线----x+y
public:
	vector<vector<string>> solveNQueens(int n)
	{
		ans.resize(n, string(n,'.'));
		backTrace(0, n);
		return ret;
	}
	void backTrace(int n, int N)
	{
		if (n == N)//最后一个皇后放置完毕
			ret.push_back(ans);
		else
		{
			//对每一列进行试探
			for (int i = 0; i<N; i++)
			{
				//如果当前放置的皇后与之前的列，左对角线或者右对角线发生冲突，那么就换下一列试探
				if (col.find(i) != col.end()||leftSlope.find(n-i)!=leftSlope.end()||rightSlope.find(n+i)!=rightSlope.end())
					continue;
				//将当前皇后放置在第n行，第i列上
				ans[n][i] = 'Q';
				//如果当前列能够放置皇后，就进行放置位置的标记
				col.insert(i);
				leftSlope.insert(n - i);
				rightSlope.insert(n + i);
				backTrace(n + 1, N);
				//如果找到了一种解，或者当前状态无解，那么恢复到上一层的状态，去寻找其他可能解
				ans[n][i] = '.';
				//撤销之前的标记
				col.erase(i);
				leftSlope.erase(n - i);
				rightSlope.erase(n + i);
			}
		}
	}
};

---

使用三个一维数组

注意使用一维数组对对角线的标记问题:

代码:

class Solution {
	vector<vector<string>> ret;//保存所有可行的八皇后放置方案结果
	vector<string> ans;//保存当前可行的八皇后放置方案
	vector<bool> col;//判断列
	vector<bool> leftSlope;//判断左对角线---x-y
	vector<bool> rightSlope;//判断右对角线----x+y
public:
	vector<vector<string>> solveNQueens(int n)
	{
		ans.resize(n, string(n,'.'));
		col.resize(n, false);
		leftSlope.resize(2*n-1,false);
		rightSlope.resize(2*n-1,false);
		backTrace(0, n);
		return ret;
	}
	void backTrace(int n, int N)
	{
		if (n == N)//最后一个皇后放置完毕
			ret.push_back(ans);
		else
		{
			//对每一列进行试探
			for (int i = 0; i<N; i++)
			{
				//如果当前放置的皇后与之前的列，左对角线或者右对角线发生冲突，那么就换下一列试探
				if (col[i]||leftSlope[N - n + i - 1]||rightSlope[n+i])//col[i]为真说明当前第i列已经放置过一个皇后了
					continue;
				//将当前皇后放置在第n行，第i列上
				ans[n][i] = 'Q';
				//如果当前列能够放置皇后，就进行放置位置的标记
				col[i]= leftSlope[N - n + i - 1]= rightSlope[n + i] = true;
				backTrace(n + 1, N);
				//如果找到了一种解，或者当前状态无解，那么恢复到上一层的状态，去寻找其他可能解
				ans[n][i] = '.';
				//撤销之前的标记
				col[i] = leftSlope[N - n + i - 1] = rightSlope[n + i] = false;
			}
		}
	}
};

---

总结

leetcode 5 1. N 皇后与本题一模一样，建议大家看完本篇文章，可以尝试去AC这两道题