力扣543：二叉树的直径C++

Posted 2021-06-17 The Gao

题目

给定一棵二叉树，你需要计算它的直径长度。一棵二叉树的直径长度是任意两个结点路径长度中的最大值。这条路径可能穿过也可能不穿过根结点。

分析

这道题的难度在LeetCode上被归为简单，但我觉得这道题无论是思路上还是代码的写法上，还有具有中等难度的程度的。

这道题要求我们计算直径长度，首先我们要将求直径长度转换成一个好求的量，笔者将求直径长度转换为求二叉树的高度。这个其实是不难理解的，因为直径其实就是经过边的个数，每经过一条边，相当于高度增加1。

但是题中说明了这条路径可能穿过根结点，因此最长的路径显然是左子树的高度+右子树的高度。

分析到这里，可能有的小伙伴会想，那这个不难呀，我用递归的方法求出左子树的高度和右子树的高度，返回它们之和就是题解了。于是写出这样的代码：

class Solution {
public:
    int diameterOfBinaryTree(TreeNode* root) {
        if(!root)return 0;
        int left=GetHeight(root->left);//求左子树高度
        int right=GetHeight(root->right);//求右子树高度
        return left+right;
    }
    int GetHeight(TreeNode* root){//递归求解高度
        if(!root)return 0;
        return 1+max(GetHeight(root->left),GetHeight(root->right));
    }
};

虽然思路是正确的，但是这样由于少考虑了一种情况而导致部分用例会出现错误。

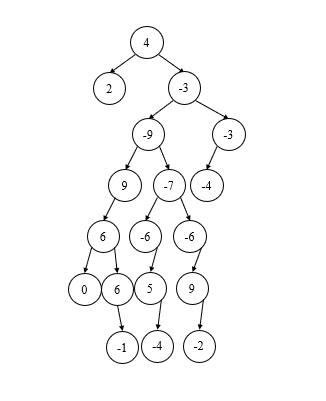
比如这个用例，按照上述代码的话，输出的答案是左子树高度1+右子树高度6=7。然而其最大路径实际上是以第三层-9这个父结点作为根结点时，此时左子树高度4+右子树高度=8。这就要求我们要结合后序遍历，实现从下往上求出每个父结点作为根结点时，左右子树高度和，并与下次求出的值作比较，保留较大值。

按照这个思路，就可以写代码了。

代码

class Solution {
    int maxlength=INT_MIN;//定义一个存储最大路径的变量
public:
    int diameterOfBinaryTree(TreeNode* root) {
        if(!root)return 0;
        dfs(root);//后序dfs
        return maxlength;        
    }
    int GetHeight(TreeNode* root){//求root高度的函数
        if(!root)return 0;
        return 1+max(GetHeight(root->left),GetHeight(root->right));
    }
    void dfs(TreeNode* root){
        if(!root)return;
        dfs(root->left);
        dfs(root->right);
        maxlength=max(maxlength,GetHeight(root->left)+GetHeight(root->right));//将maxlength与当前父结点左右子树高度和比较，保留较大值
    }
};