图像分割基于模糊聚类算法FCM实现图像分割matlab源码

Posted 2021-06-16 MatlabQQ1575304183

 伴随着模糊集理论的形成、发展和深化，RusPini率先提出模糊划分的概念。以此为起点和基础，模糊聚类理论和方法迅速蓬勃发展起来。针对不同的应用，人们提出了很多模糊聚类算法，比较典型的有基于相似性关系和模糊关系的方法、基于模糊等价关系的传递闭包方法、基于模糊图论的最大支撑树方法，以及基于数据集的凸分解、动态规划和难以辨别关系等方法。然而，上述方法均不能适用于大数据量的情况，难以满足实时性要求较高的场合，因此实际应用并不广泛。

模糊聚类分析按照聚类过程的不同大致可以分为三大类：

(1)基于模糊关系的分类法：其中包括谱系聚类算法(又称系统聚类法)、基于等价关系的聚类算法、基于相似关系的聚类算法和图论聚类算法等等。它是研究比较早的一种方法，但是由于它不能适用于大数据量的情况，所以在实际中的应用并不广泛。

(2)基于目标函数的模糊聚类算法：该方法把聚类分析归结成一个带约束的非线性规划问题，通过优化求解获得数据集的最优模糊划分和聚类。该方法设计简单、解决问题的范围广，还可以转化为优化问题而借助经典数学的非线性规划理论求解，并易于计算机实现。因此，随着计算机的应用和发展，基于目标函数的模糊聚类算法成为新的研究热点。

(3)基于神经网络的模糊聚类算法：它是兴起比较晚的一种算法，主要是采用竞争学习算法来指导网络的聚类过程。

 

在介绍算法之前，先介绍下模糊集合的知识。

HCM聚类算法

        首先说明隶属度函数的概念。隶属度函数是表示一个对象x 隶属于集合A 的程度的函数，通常记做μA(x)，其自变量范围是所有可能属于集合A 的对象（即集合A 所在空间中的所有点），取值范围是[0,1]，即0<=μA(x)，μA(x)<=1。μA(x)=1 表示x 完全隶属于集合A，相当于传统集合概念上的x∈A。一个定义在空间X={x}上的隶属度函数就定义了一个模糊集合A，或者叫定义在论域X={x}上的模糊子集A’。对于有限个对象x1，x2，……，xn 模糊集合A’可以表示为：

 

        有了模糊集合的概念，一个元素隶属于模糊集合就不是硬性的了，在聚类的问题中，可以把聚类生成的簇看成模糊集合，因此，每个样本点隶属于簇的隶属度就是[0，1]区间里面的值。

 

再接下来要讲FCM算法不得不先讲一下HCM算法

硬C-均值(HCM)算法是实现数据集J硬C划分的经典算法之一，也是最受欢迎的算法之一。它能够把数据集X分成C个超椭球结构的聚类。HCM算法把传统的聚类问题归结为如下的非线性数学规划问题：

 

其中U=(uij)cxn为硬C-划分矩阵，V=(v1，v2，，，vc)为C个聚类中心，||·||代码欧式距离。

HCM算法的具体流程如下：

初始化：指定聚类类别数C，2<=C<=n，n是数据个数，设定迭代停止阈值Ɛ，初始化聚类中心V0，设置迭代计数器b=0；

步骤一：根据下面的公式计算或更新划分矩阵U

 

步骤二：根据下面公式更新聚类中心V（b+1）

 

步骤三：如果||Vb – V(b+1)||< Ɛ，则算法停止并输出划分矩阵和聚类中心V，否则令b=b+1，转向执行步骤一

FCM聚类算法

Dunn按照RusPini定义的模糊划分的概念，把HCM算法扩展到模糊划分领域。Dunn对每个样本与每个聚类中心的距离用其隶属度平方加权，从而把类内误差平方和目标函数J1扩展为类内加权误差平方和函数J2：

 

Bezdek又将Dunn的目标函数推广为更普遍的形式，给出了基于目标函数的模糊聚类更一般的描述。

 

其中，m∈[1,+∞)称为加权指数，又称作平滑参数。尽管从数学角度看，m的出现不自然，但如果不对隶属度加权，从HCM算法到FCM算法的推广将是无效的。

FCM算法的具体流程如下：

初始化：指定聚类类别数C，2<=C<=n，n是数据个数，设定迭代停止阈值Ɛ，初始化聚类中心V0，设置迭代计数器b=0；

步骤一：根据下面的公式计算或更新划分矩阵U

 

步骤二：根据下面公式更新聚类中心V（b+1）

 

步骤三：如果||Vb – V(b+1)||< Ɛ，则算法停止并输出划分矩阵和聚类中心V，否则令b=b+1，转向执行步骤一

 

FCM算法流程图

FCM算法是目前比较流行的一种模糊聚类算法，究其原因大致有以下几个方面：首先，模糊C—均值泛函Jm仍是传统硬C一均值泛函J1的自然推广；硬C一均值泛函J1是一个应用十分广泛的聚类准则，对其在理论上的研究己经相当完善，这就为Jm的研究提供了良好的条件；数学上看，Jm与RS的希尔伯特空间结构(正交投影和均方逼近理论)有密切的关系，因此比其它泛函有更深厚的数学基础；最后，也是最重要的是该目标函数不仅在许多领域获得了非常成功的应用，而且以FCM算法为基础，人们提出的基于其它原型的模糊聚类算法，形成了一大批FCM类型的算法：如模糊C一线(FCL)、模糊C一面(FCP)等聚类算法，分别实现了对呈线状、超平面状结构模式子集(或聚类)的检测。

FCM算法应用到颜色迁移中

        钱小燕等人将聚类算法应用到色彩迁移中，提出了一种基于图像模糊颜色聚类的自适应色彩迁移算法。该算法首先将源图像和目标图像分别转换到lαβ颜色空间：利用FCM 算法把源图像和目标图像划分为具有不同颜色特征的聚类，然后分析图像中的颜色特征：分别算出每个域的匹配权值，对每个目标图像的匹配权值，从源图像中选取一个最接近域作为最佳匹配域；最后根据目标图像各聚类域与源图像中的匹配域之间的关系，引入隶属度因子，两个域的处理结果分别进行加权平均，获得色彩迁移结果。使用FCM的思想对图像进行聚类域划分的思路是：设准备处理图像I的大小是S×H，即对颜色聚类颜色分析的个数是N，N = S×H，则图像I可表示成集合，I={p1 ,p2 ...,pn }。图像被分为c类，每个类的聚类中心为V={v1,v2 ...,vc }，用uik表示像素pk隶属于聚类中心Vi的隶属度，定义图像的隶属度矩阵U。具体算法如下：

步骤一：把源图像和目标图像分别从RGB转换到lαβ空间。

步骤二：确定待处理图像聚类域个数c，然后初始化聚类中心。假设加权指数m=2，设定处理的最大迭代次数为50。

步骤三：当迭代次数T 小于50 时，根据初始化聚类中心计算隶属度矩阵。如果pk≠vi,则对于所有的vi ( i=1,2,...,C )，利用下式计算隶属度矩阵。

 

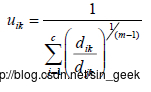
其中，i =1,2,...C； j =1,2,...N

如果，pk=vi,，k =1,2,...N则

 

其中，dik为第k个元素到第i 个聚类中心的距离，定义在lαβ下的欧式距离。

 

步骤四：对图像聚类划分。图像的隶属度矩阵中，从每列选择隶属度最大的点作为相对应点的归属域，并重新计算聚类中心。

步骤五：对收敛情况进行检查。若||Vi – V’i||<Σ，则立即停止迭代；否则一直迭代计算步骤三与步骤四。

步骤六：对聚类域进行匹配。使用FCM 后，对每一个聚类域分别设置一个匹配权值参数w，当目标图像是灰度图像时，w为聚类域的亮度均值；当目标图像为彩色图像时，w 是聚类域3 个通道标准差的加权平均值。

步骤七：色彩迁移。为了保持通用性，假定目标图像中元素pi的归属域与源图像中聚类域h 是匹配域，利用下式获得各个通道的新值：

 

%% 程序分享 

%--------------------------------------

clear
close all
clc
%% %%%%%%%%%%%%%%%图像%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
 I=imread('3096.jpg');

if size(I,3) == 3
   I=rgb2gray(I);
else
end
I=im2double(I);
figure;imshow(I);title('(a)原始图像')
% I=I;%不加噪声
%I=imnoise(I,'speckle',deta_2);
% I=imnoise(I,'salt & pepper',0.05); %加噪图
% I=imnoise(I,'gaussian',0,0.01); % 加高斯噪声
figure;imshow(I);title('(b)加噪图像');
imwrite(I,'2.jpg');
[m,n]=size(I);
%k 聚类数目
k=2;
% k=3;

I4 = I(:);  %% 将图像灰度按列排列
%% ------------------------ fcm算法------------------------
fcm_spatial_mean_label=zeros(m*n,1);
t=cputime;
tic;
[O2, U2, obj_fcn2] = fcm(I4, k);
toc;
time_fcm_spatial_mean=cputime-t;
%% 最大隶属度原则
maxU2 = max(U2);   %隶属度最大  
for j=1:k
    index = find(U2(j, :) == maxU2);  %隶属度最大对应的像素位置
    fcm_spatial_mean_label(index) = j;    
end
labels2=reshape(fcm_spatial_mean_label,[m n]);
labels2=uint16(labels2);

%% 显示聚类分割图
labels2(find(labels2==1))=0;
labels2(find(labels2==2))=255;
labels2(find(labels2==3))=180;
labels2(find(labels2==4))=100;
labels2=uint8(labels2);
figure;imshow(labels2,[]);title('(c)聚类分割图');
imwrite(labels2,'3.1.tiff','tiff','Resolution',300);%输出结果，保存为tif图片

完整代码添加QQ1575304183