2_深度学习知识点

Posted 2021-06-15 to.to

以下转自：https://zhuanlan.zhihu.com/p/39367605

1.CNN的卷积核是单层的还是多层的？

解析：

一般而言，深度卷积网络是一层又一层的。层的本质是特征图, 存贮输入数据或其中间表示值。一组卷积核则是联系前后两层的网络参数表达体, 训练的目标就是每个卷积核的权重参数组。

描述网络模型中某层的厚度，通常用名词通道channel数或者特征图feature map数。不过人们更习惯把作为数据输入的前层的厚度称之为通道数（比如RGB三色图层称为输入通道数为3），把作为卷积输出的后层的厚度称之为特征图数。

卷积核(filter)一般是3D多层的，除了面积参数, 比如3x3之外, 还有厚度参数H（2D的视为厚度1). 还有一个属性是卷积核的个数N。

卷积核的厚度H, 一般等于前层厚度M(输入通道数或feature map数). 特殊情况M > H。

卷积核的个数N, 一般等于后层厚度(后层feature maps数，因为相等所以也用N表示)。

卷积核通常从属于后层，为后层提供了各种查看前层特征的视角，这个视角是自动形成的。

卷积核厚度等于1时为2D卷积，对应平面点相乘然后把结果加起来，相当于点积运算；

卷积核厚度大于1时为3D卷积，每片分别平面点求卷积，然后把每片结果加起来，作为3D卷积结果；1x1卷积属于3D卷积的

一个特例，有厚度无面积, 直接把每片单个点乘以权重再相加。

归纳之，卷积的意思就是把一个区域，不管是一维线段，二维方阵，还是三维长方块，全部按照卷积核的维度形状，对应逐点相乘再求和，浓缩成一个标量值也就是降到零维度，作为下一层的一个feature map的一个点的值！

可以比喻一群渔夫坐一个渔船撒网打鱼，鱼塘是多层水域，每层鱼儿不同。

船每次移位一个stride到一个地方，每个渔夫撒一网，得到收获，然后换一个距离stride再撒，如此重复直到遍历鱼塘。

A渔夫盯着鱼的品种，遍历鱼塘后该渔夫描绘了鱼塘的鱼品种分布；

B渔夫盯着鱼的重量，遍历鱼塘后该渔夫描绘了鱼塘的鱼重量分布；

还有N-2个渔夫，各自兴趣各干各的；

最后得到N个特征图，描述了鱼塘的一切！

2D卷积表示渔夫的网就是带一圈浮标的渔网，只打上面一层水体的鱼；

3D卷积表示渔夫的网是多层嵌套的渔网，上中下层水体的鱼儿都跑不掉；

1x1卷积可以视为每次移位stride，甩钩钓鱼代替了撒网；

下面解释一下特殊情况的 M > H：

实际上，除了输入数据的通道数比较少之外，中间层的feature map数很多，这样中间层算卷积会累死计算机（鱼塘太深，每层鱼都打，需要的鱼网太重了）。所以很多深度卷积网络把全部通道/特征图划分一下，每个卷积核只看其中一部分（渔夫A的渔网只打捞深水段，渔夫B的渔网只打捞浅水段）。这样整个深度网络架构是横向开始分道扬镳了，到最后才又融合。这样看来，很多网络模型的架构不完全是突发奇想，而是是被参数计算量逼得。特别是现在需要在移动设备上进行AI应用计算(也叫推断), 模型参数规模必须更小, 所以出现很多减少握手规模的卷积形式, 现在主流网络架构大都如此。

2.什么是卷积？

解析：
对图像（不同的数据窗口数据）和滤波矩阵（一组固定的权重：因为每个神经元的多个权重固定，所以又可以看做一个恒定的滤波器filter）做内积（逐个元素相乘再求和）的操作就是所谓的『卷积』操作，也是卷积神经网络的名字来源。

非严格意义上来讲，下图中红框框起来的部分便可以理解为一个滤波器，即带着一组固定权重的神经元。多个滤波器叠加便成了卷积层。

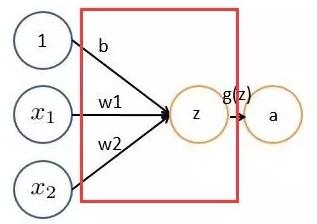
OK，举个具体的例子。比如下图中，图中左边部分是原始输入数据，图中中间部分是滤波器filter，图中右边是输出的新的二维数据。


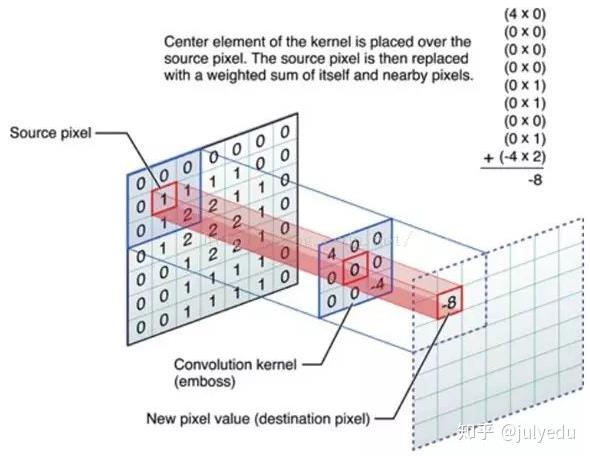
中间滤波器filter与数据窗口做内积，其具体计算过程则是：40 + 00 + 00 + 00 + 01 + 01 + 00 + 01 + -4*2 = -8

3.什么是CNN的池化pool层？

解析：
池化，简言之，即取区域平均或最大，如下图所示（图引自cs231n）

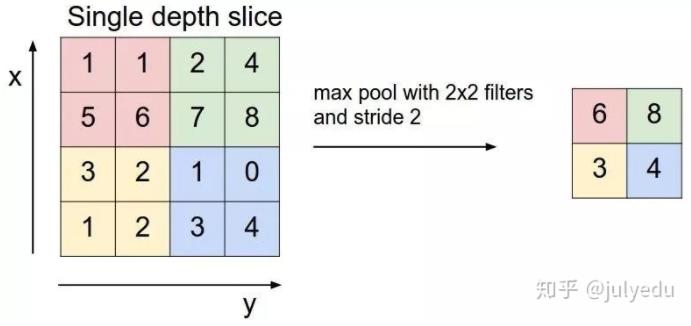
上图所展示的是取区域最大，即上图左边部分中 左上角2x2的矩阵中6最大，右上角2x2的矩阵中8最大，左下角2x2的矩阵中3最大，右下角2x2的矩阵中4最大，所以得到上图右边部分的结果：6 8 3 4。

4.简述下什么是生成对抗网络。

解析：
GAN之所以是对抗的，是因为GAN的内部是竞争关系，一方叫generator，它的主要工作是生成图片，并且尽量使得其看上去是来自于训练样本的。另一方是discriminator，其目标是判断输入图片是否属于真实训练样本。

更直白的讲，将generator想象成假币制造商，而discriminator是警察。generator目的是尽可能把假币造的跟真的一样，从而能够骗过discriminator，即生成样本并使它看上去好像来自于真实训练样本一样。

如下图中的左右两个场景：

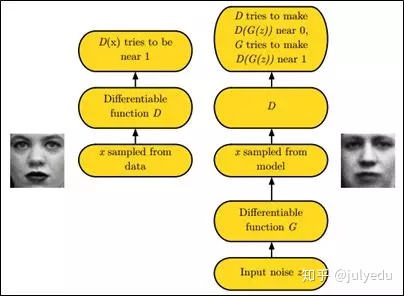
更多请参见此课程：《生成对抗网络班》（链接：https://www.julyedu.com/course/getDetail/83）

---

以下转自：https://zhuanlan.zhihu.com/p/39533743

1、为什么引入非线性激励函数？

解析：
第一，对于神经网络来说，网络的每一层相当于f(wx+b)=f(w’x)，对于线性函数，其实相当于f(x)=x，那么在线性激活函数下，每一层相当于用一个矩阵去乘以x，那么多层就是反复的用矩阵去乘以输入。根据矩阵的乘法法则，多个矩阵相乘得到一个大矩阵。所以线性激励函数下，多层网络与一层网络相当。比如，两层的网络f(W1*f(W2x))=W1W2x=Wx。

第二，非线性变换是深度学习有效的原因之一。原因在于非线性相当于对空间进行变换，变换完成后相当于对问题空间进行简化，原来线性不可解的问题现在变得可以解了。

下图可以很形象的解释这个问题，左图用一根线是无法划分的。经过一系列变换后，就变成线性可解的问题了。

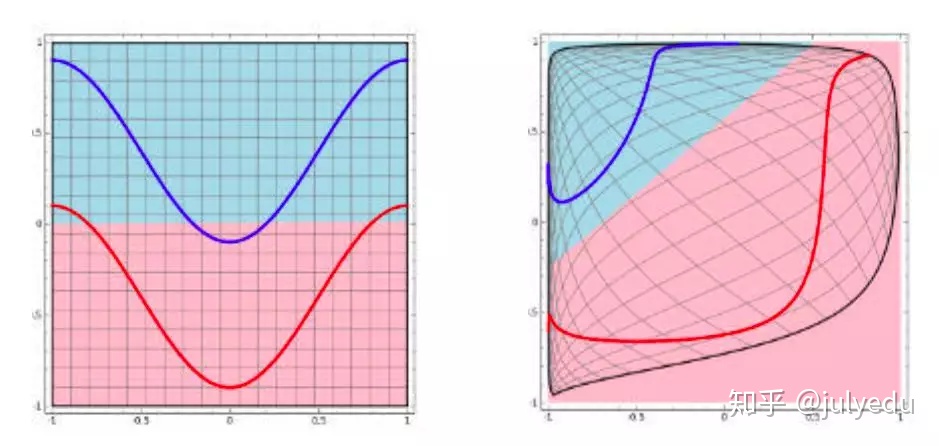
如果不用激励函数（其实相当于激励函数是f(x) = x），在这种情况下你每一层输出都是上层输入的线性函数，很容易验证，无论你神经网络有多少层，输出都是输入的线性组合，与没有隐藏层效果相当，这种情况就是最原始的感知机（Perceptron）了。

正因为上面的原因，我们决定引入非线性函数作为激励函数，这样深层神经网络就有意义了（不再是输入的线性组合，可以逼近任意函数）。最早的想法是sigmoid函数或者tanh函数，输出有界，很容易充当下一层输入（以及一些人的生物解释）。

4、如何解决RNN梯度爆炸和弥散的问题？

解析：
为了解决梯度爆炸问题，Thomas Mikolov首先提出了一个简单的启发性的解决方案，就是当梯度大于一定阈值的的时候，将它截断为一个较小的数。具体如算法1所述：
算法：当梯度爆炸时截断梯度（伪代码）

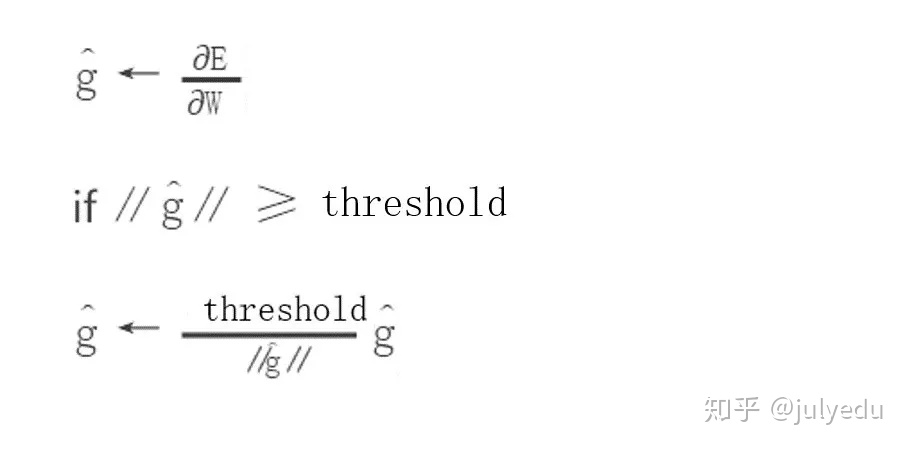
下图可视化了梯度截断的效果。它展示了一个小的rnn（其中W为权值矩阵，b为bias项）的决策面。这个模型是一个一小段时间的rnn单元组成；实心箭头表明每步梯度下降的训练过程。当梯度下降过程中，模型的目标函数取得了较高的误差时，梯度将被送到远离决策面的位置。截断模型产生了一个虚线，它将误差梯度拉回到离原始梯度接近的位置。

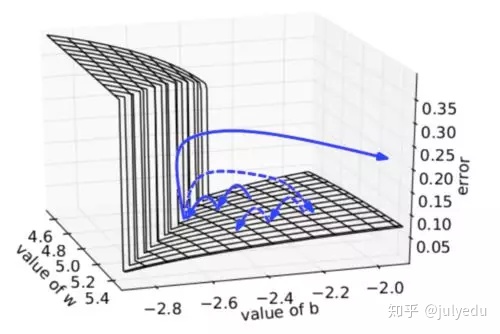
梯度爆炸，梯度截断可视化
为了解决梯度弥散的问题，我们介绍了两种方法。第一种方法是将随机初始化

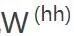
改为一个有关联的矩阵初始化。第二种方法是使用ReLU（Rectified Linear Units）代替sigmoid函数。ReLU的导数不是0就是1.因此，神经元的梯度将始终为1，而不会当梯度传播了一定时间之后变小。

5、什麽样的资料集不适合用深度学习？

解析：
（1）数据集太小，数据样本不足时，深度学习相对其它机器学习算法，没有明显优势。
（2）数据集没有局部相关特性，目前深度学习表现比较好的领域主要是图像／语音／自然语言处理等领域，这些领域的一个共性是局部相关性。图像中像素组成物体，语音信号中音位组合成单词，文本数据中单词组合成句子，这些特征元素的组合一旦被打乱，表示的含义同时也被改变。对于没有这样的局部相关性的数据集，不适于使用深度学习算法进行处理。举个例子：预测一个人的健康状况，相关的参数会有年龄、职业、收入、家庭状况等各种元素，将这些元素打乱，并不会影响相关的结果。

---

以下转自：https://zhuanlan.zhihu.com/p/39619083

1.广义线性模型是怎被应用在深度学习中？

解析：
A Statistical View of Deep Learning (I): Recursive GLMs

深度学习从统计学角度，可以看做递归的广义线性模型。

广义线性模型相对于经典的线性模型(y=wx+b)，核心在于引入了连接函数g(.)，形式变为：y=g−1(wx+b)。

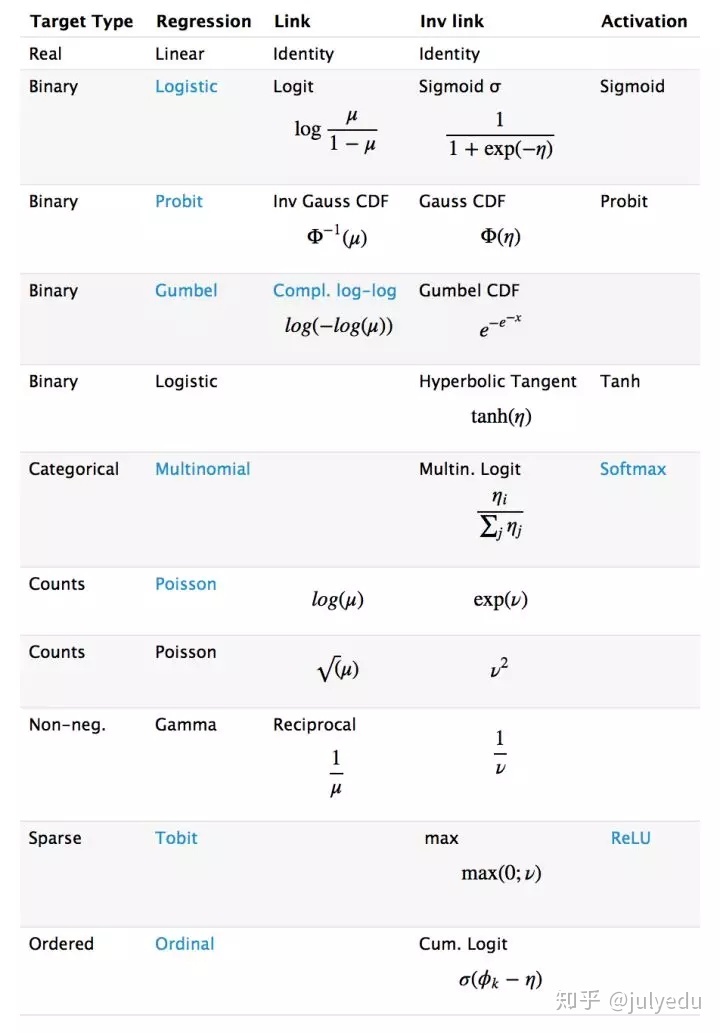
深度学习时递归的广义线性模型，神经元的激活函数，即为广义线性模型的链接函数。逻辑回归（广义线性模型的一种）的Logistic函数即为神经元激活函数中的Sigmoid函数，很多类似的方法在统计学和神经网络中的名称不一样，容易引起初学者（这里主要指我）的困惑。

下图是一个对照表：

2.如何解决梯度消失和梯度膨胀？

解析：
（1）梯度消失：
根据链式法则，如果每一层神经元对上一层的输出的偏导乘上权重结果都小于1的话，那么即使这个结果是0.99，在经过足够多层传播之后，误差对输入层的偏导会趋于0

可以采用ReLU激活函数有效的解决梯度消失的情况，也可以用Batch Normalization解决这个问题。关于深度学习中 Batch Normalization为什么效果好？

（2）梯度膨胀
根据链式法则，如果每一层神经元对上一层的输出的偏导乘上权重结果都大于1的话，在经过足够多层传播之后，误差对输入层的偏导会趋于无穷大

可以通过激活函数来解决，或用Batch Normalization解决这个问题。

3.简述神经网络的发展历史。

解析：
1949年Hebb提出了神经心理学学习范式——Hebbian学习理论
1952年，IBM的Arthur Samuel写出了西洋棋程序
1957年，Rosenblatt的感知器算法是第二个有着神经系统科学背景的机器学习模型.

3年之后，Widrow因发明Delta学习规则而载入ML史册，该规则马上就很好的应用到了感知器的训练中

感知器的热度在1969被Minskey一盆冷水泼灭了。他提出了著名的XOR问题，论证了感知器在类似XOR问题的线性不可分数据的无力。

尽管BP的思想在70年代就被Linnainmaa以“自动微分的翻转模式”被提出来，但直到1981年才被Werbos应用到多层感知器(MLP)中，NN新的大繁荣。

1991年的Hochreiter和2001年的Hochreiter的工作，都表明在使用BP算法时，NN单元饱和之后会发生梯度损失。又发生停滞。

时间终于走到了当下，随着计算资源的增长和数据量的增长。一个新的NN领域——深度学习出现了。

简言之，MP模型+sgn—->单层感知机（只能线性）+sgn— Minsky 低谷 —>多层感知机+BP+sigmoid—- (低谷) —>深度学习+pre-training+ReLU/sigmoid

4.深度学习常用方法。

解析：
全连接DNN（相邻层相互连接、层内无连接）：

AutoEncoder(尽可能还原输入)、Sparse Coding（在AE上加入L1规范）、RBM（解决概率问题）—–>特征探测器——>栈式叠加 贪心训练

RBM—->DBN

解决全连接DNN的全连接问题—–>CNN

解决全连接DNN的无法对时间序列上变化进行建模的问题—–>RNN—解决时间轴上的梯度消失问题——->LSTM

DNN是传统的全连接网络，可以用于广告点击率预估，推荐等。其使用embedding的方式将很多离散的特征编码到神经网络中，可以很大的提升结果。

CNN主要用于计算机视觉(Computer Vision)领域，CNN的出现主要解决了DNN在图像领域中参数过多的问题。同时，CNN特有的卷积、池化、batch normalization、Inception、ResNet、DeepNet等一系列的发展也使得在分类、物体检测、人脸识别、图像分割等众多领域有了长足的进步。同时，CNN不仅在图像上应用很多，在自然语言处理上也颇有进展，现在已经有基于CNN的语言模型能够达到比LSTM更好的效果。在最新的AlphaZero中，CNN中的ResNet也是两种基本算法之一。

GAN是一种应用在生成模型的训练方法，现在有很多在CV方面的应用，例如图像翻译，图像超清化、图像修复等等。

RNN主要用于自然语言处理(Natural Language Processing)领域，用于处理序列到序列的问题。普通RNN会遇到梯度爆炸和梯度消失的问题。所以现在在NLP领域，一般会使用LSTM模型。在最近的机器翻译领域，Attention作为一种新的手段，也被引入进来。

除了DNN、RNN和CNN外， 自动编码器(AutoEncoder)、稀疏编码(Sparse Coding)、深度信念网络(DBM)、限制玻尔兹曼机(RBM)也都有相应的研究。

5.请简述神经网络的发展史。

解析：
sigmoid会饱和，造成梯度消失。于是有了ReLU。
ReLU负半轴是死区，造成梯度变0。于是有了LeakyReLU，PReLU。
强调梯度和权值分布的稳定性，由此有了ELU，以及较新的SELU。
太深了，梯度传不下去，于是有了highway。
干脆连highway的参数都不要，直接变残差，于是有了ResNet。
强行稳定参数的均值和方差，于是有了BatchNorm。
在梯度流中增加噪声，于是有了 Dropout。
RNN梯度不稳定，于是加几个通路和门控，于是有了LSTM。
LSTM简化一下，有了GRU。
GAN的JS散度有问题，会导致梯度消失或无效，于是有了WGAN。
WGAN对梯度的clip有问题，于是有了WGAN-GP。

---

以下转自：https://zhuanlan.zhihu.com/p/39703500

26.神经网络中激活函数的真正意义？一个激活函数需要具有哪些必要的属性？还有哪些属性是好的属性但不必要的？

解析：

（1）非线性：即导数不是常数。这个条件是多层神经网络的基础，保证多层网络不退化成单层线性网络。这也是激活函数的意义所在。

（2）几乎处处可微：可微性保证了在优化中梯度的可计算性。传统的激活函数如sigmoid等满足处处可微。对于分段线性函数比如ReLU，只满足几乎处处可微（即仅在有限个点处不可微）。对于SGD算法来说，由于几乎不可能收敛到梯度接近零的位置，有限的不可微点对于优化结果不会有很大影响[1]。

（3）计算简单：非线性函数有很多。极端的说，一个多层神经网络也可以作为一个非线性函数，类似于Network In Network[2]中把它当做卷积操作的做法。但激活函数在神经网络前向的计算次数与神经元的个数成正比，因此简单的非线性函数自然更适合用作激活函数。这也是ReLU之流比其它使用Exp等操作的激活函数更受欢迎的其中一个原因。

（4）非饱和性（saturation）：饱和指的是在某些区间梯度接近于零（即梯度消失），使得参数无法继续更新的问题。最经典的例子是Sigmoid，它的导数在x为比较大的正值和比较小的负值时都会接近于0。更极端的例子是阶跃函数，由于它在几乎所有位置的梯度都为0，因此处处饱和，无法作为激活函数。ReLU在x>0时导数恒为1，因此对于再大的正值也不会饱和。但同时对于x<0，其梯度恒为0，这时候它也会出现饱和的现象（在这种情况下通常称为dying ReLU）。Leaky ReLU[3]和PReLU[4]的提出正是为了解决这一问题。

（5）单调性（monotonic）：即导数符号不变。这个性质大部分激活函数都有，除了诸如sin、cos等。个人理解，单调性使得在激活函数处的梯度方向不会经常改变，从而让训练更容易收敛。

（6）输出范围有限：有限的输出范围使得网络对于一些比较大的输入也会比较稳定，这也是为什么早期的激活函数都以此类函数为主，如Sigmoid、TanH。但这导致了前面提到的梯度消失问题，而且强行让每一层的输出限制到固定范围会限制其表达能力。因此现在这类函数仅用于某些需要特定输出范围的场合，比如概率输出（此时loss函数中的log操作能够抵消其梯度消失的影响[1]）、LSTM里的gate函数。

（7）接近恒等变换（identity）：即约等于x。这样的好处是使得输出的幅值不会随着深度的增加而发生显著的增加，从而使网络更为稳定，同时梯度也能够更容易地回传。这个与非线性是有点矛盾的，因此激活函数基本只是部分满足这个条件，比如TanH只在原点附近有线性区（在原点为0且在原点的导数为1），而ReLU只在x>0时为线性。这个性质也让初始化参数范围的推导更为简单[5][4]。额外提一句，这种恒等变换的性质也被其他一些网络结构设计所借鉴，比如CNN中的ResNet[6]和RNN中的LSTM。

（8）参数少：大部分激活函数都是没有参数的。像PReLU带单个参数会略微增加网络的大小。还有一个例外是Maxout[7]，尽管本身没有参数，但在同样输出通道数下k路Maxout需要的输入通道数是其它函数的k倍，这意味着神经元数目也需要变为k倍；但如果不考虑维持输出通道数的情况下，该激活函数又能将参数个数减少为原来的k倍。

（9）归一化（normalization）：这个是最近才出来的概念，对应的激活函数是SELU[8]，主要思想是使样本分布自动归一化到零均值、单位方差的分布，从而稳定训练。在这之前，这种归一化的思想也被用于网络结构的设计，比如Batch Normalization[9]。

27.梯度下降法的神经网络容易收敛到局部最优，为什么应用广泛？

解析：
深度神经网络“容易收敛到局部最优”，很可能是一种想象，实际情况是，我们可能从来没有找到过“局部最优”，更别说全局最优了。
很多人都有一种看法，就是“局部最优是神经网络优化的主要难点”。这来源于一维优化问题的直观想象。在单变量的情形下，优化问题最直观的困难就是有很多局部极值，如

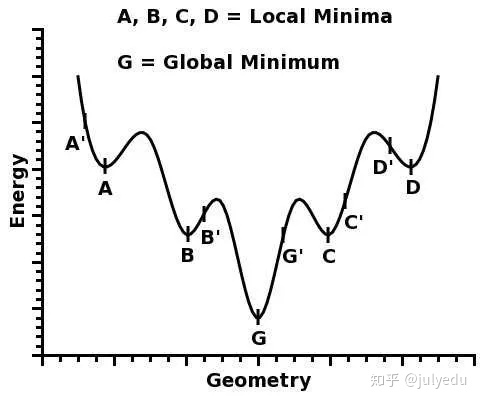
人们直观的想象，高维的时候这样的局部极值会更多，指数级的增加，于是优化到全局最优就更难了。然而单变量到多变量一个重要差异是，单变量的时候，Hessian矩阵只有一个特征值，于是无论这个特征值的符号正负，一个临界点都是局部极值。但是在多变量的时候，Hessian有多个不同的特征值，这时候各个特征值就可能会有更复杂的分布，如有正有负的不定型和有多个退化特征值（零特征值）的半定型

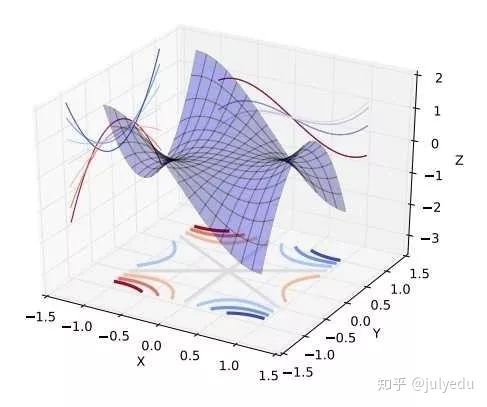
在后两种情况下，是很难找到局部极值的，更别说全局最优了。

现在看来，神经网络的训练的困难主要是鞍点的问题。在实际中，我们很可能也从来没有真的遇到过局部极值。Bengio组这篇文章Eigenvalues of the Hessian in Deep Learning（https://arxiv.org/abs/1611.07476）里面的实验研究给出以下的结论：

• Training stops at a point that has a small gradient. The norm of the gradient is not zero, therefore it does not, technically speaking, converge to a critical point.

• There are still negative eigenvalues even when they are small in magnitude.

另一方面，一个好消息是，即使有局部极值，具有较差的loss的局部极值的吸引域也是很小的Towards Understanding Generalization of Deep Learning: Perspective of Loss Landscapes。（https://arxiv.org/abs/1706.10239）

For the landscape of loss function for deep networks, the volume of basin of attraction of good minima dominates over that of poor minima, which guarantees optimization methods with random initialization to converge to good minima.

所以，很可能我们实际上是在“什么也没找到”的情况下就停止了训练，然后拿到测试集上试试，“咦，效果还不错”。

补充说明，这些都是实验研究结果。理论方面，各种假设下，深度神经网络的Landscape 的鞍点数目指数增加，而具有较差loss的局部极值非常少。

28.简单说说CNN常用的几个模型。

解析：

29.为什么很多做人脸的Paper会最后加入一个Local Connected Conv？

解析：
以FaceBook DeepFace 为例：

DeepFace 先进行了两次全卷积＋一次池化，提取了低层次的边缘／纹理等特征。后接了3个Local-Conv层，这里是用Local-Conv的原因是，人脸在不同的区域存在不同的特征（眼睛／鼻子／嘴的分布位置相对固定），当不存在全局的局部特征分布时，Local-Conv更适合特征的提取。

30.什么是梯度爆炸？

解析：
误差梯度是神经网络训练过程中计算的方向和数量，用于以正确的方向和合适的量更新网络权重。

在深层网络或循环神经网络中，误差梯度可在更新中累积，变成非常大的梯度，然后导致网络权重的大幅更新，并因此使网络变得不稳定。在极端情况下，权重的值变得非常大，以至于溢出，导致 NaN 值。

网络层之间的梯度（值大于 1.0）重复相乘导致的指数级增长会产生梯度爆炸。

---

以下转自：https://zhuanlan.zhihu.com/p/39881106

31.梯度爆炸会引发什么问题？

解析：
在深度多层感知机网络中，梯度爆炸会引起网络不稳定，最好的结果是无法从训练数据中学习，而最坏的结果是出现无法再更新的 NaN 权重值。

梯度爆炸导致学习过程不稳定。—《深度学习》，2016。

在循环神经网络中，梯度爆炸会导致网络不稳定，无法利用训练数据学习，最好的结果是网络无法学习长的输入序列数据。

32.如何确定是否出现梯度爆炸？

解析：
训练过程中出现梯度爆炸会伴随一些细微的信号，如：

模型无法从训练数据中获得更新（如低损失）。

模型不稳定，导致更新过程中的损失出现显著变化。

训练过程中，模型损失变成 NaN。

如果你发现这些问题，那么你需要仔细查看是否出现梯度爆炸问题。

以下是一些稍微明显一点的信号，有助于确认是否出现梯度爆炸问题。

训练过程中模型梯度快速变大。

训练过程中模型权重变成 NaN 值。

训练过程中，每个节点和层的误差梯度值持续超过 1.0。

33.如何修复梯度爆炸问题？

解析：

有很多方法可以解决梯度爆炸问题，本节列举了一些最佳实验方法。

（1） 重新设计网络模型

在深度神经网络中，梯度爆炸可以通过重新设计层数更少的网络来解决。

使用更小的批尺寸对网络训练也有好处。

在循环神经网络中，训练过程中在更少的先前时间步上进行更新（沿时间的截断反向传播，truncated Backpropagation through time）可以缓解梯度爆炸问题。

（2）使用 ReLU 激活函数

在深度多层感知机神经网络中，梯度爆炸的发生可能是因为激活函数，如之前很流行的 Sigmoid 和 Tanh 函数。

使用 ReLU 激活函数可以减少梯度爆炸。采用 ReLU 激活函数是最适合隐藏层的新实践。

（3）使用长短期记忆网络

在循环神经网络中，梯度爆炸的发生可能是因为某种网络的训练本身就存在不稳定性，如随时间的反向传播本质上将循环网络转换成深度多层感知机神经网络。

使用长短期记忆（LSTM）单元和相关的门类型神经元结构可以减少梯度爆炸问题。

采用 LSTM 单元是适合循环神经网络的序列预测的最新最好实践。

（4）使用梯度截断（Gradient Clipping）

在非常深且批尺寸较大的多层感知机网络和输入序列较长的 LSTM 中，仍然有可能出现梯度爆炸。如果梯度爆炸仍然出现，你可以在训练过程中检查和限制梯度的大小。这就是梯度截断。

处理梯度爆炸有一个简单有效的解决方案：如果梯度超过阈值，就截断它们。

——《Neural Network Methods in Natural Language Processing》，2017.

具体来说，检查误差梯度的值是否超过阈值，如果超过，则截断梯度，将梯度设置为阈值。

梯度截断可以一定程度上缓解梯度爆炸问题（梯度截断，即在执行梯度下降步骤之前将梯度设置为阈值）。

——《深度学习》，2016.

在 Keras 深度学习库中，你可以在训练之前设置优化器上的 clipnorm 或 clipvalue 参数，来使用梯度截断。

默认值为 clipnorm=1.0 、clipvalue=0.5。详见：https://keras.io/optimizers/。

（5）使用权重正则化（Weight Regularization）

如果梯度爆炸仍然存在，可以尝试另一种方法，即检查网络权重的大小，并惩罚产生较大权重值的损失函数。该过程被称为权重正则化，通常使用的是 L1 惩罚项（权重绝对值）或 L2 惩罚项（权重平方）。

对循环权重使用 L1 或 L2 惩罚项有助于缓解梯度爆炸。

——On the difficulty of training recurrent neural networks，2013.

在 Keras 深度学习库中，你可以通过在层上设置 kernel_regularizer 参数和使用 L1 或 L2 正则化项进行权重正则化。

34.LSTM神经网络输入输出究竟是怎样的？

解析：
第一要明确的是神经网络所处理的单位全部都是：向量

下面就解释为什么你会看到训练数据会是矩阵和张量

常规feedforward 输入和输出：矩阵

输入矩阵形状：(n_samples, dim_input)

输出矩阵形状：(n_samples, dim_output)

注：真正测试/训练的时候，网络的输入和输出就是向量而已。加入n_samples这个维度是为了可以实现一次训练多个样本，求出平均梯度来更新权重，这个叫做Mini-batch gradient descent。 如果n_samples等于1，那么这种更新方式叫做Stochastic Gradient Descent (SGD)。

Feedforward 的输入输出的本质都是单个向量。

常规Recurrent (RNN/LSTM/GRU) 输入和输出：张量

输入张量形状：(time_steps, n_samples, dim_input)

输出张量形状：(time_steps, n_samples, dim_output)

注：同样是保留了Mini-batch gradient descent的训练方式，但不同之处在于多了time step这个维度。

Recurrent 的任意时刻的输入的本质还是单个向量，只不过是将不同时刻的向量按顺序输入网络。所以你可能更愿意理解为一串向量 a sequence of vectors，或者是矩阵。

python代码表示预测的话：

import numpy as np

#当前所累积的hidden_state,若是最初的vector，则hidden_state全为0

hidden_state=np.zeros((n_samples, dim_input))

#print(inputs.shape)： （time_steps, n_samples, dim_input)

outputs = np.zeros((time_steps, n_samples, dim_output))

for i in range(time_steps):

#输出当前时刻的output，同时更新当前已累积的hidden_state

outputs[i],hidden_state = RNN.predict(inputs[i],hidden_state)

#print(outputs.shape)： (time_steps, n_samples, dim_output)

但需要注意的是，Recurrent nets的输出也可以是矩阵，而非三维张量，取决于你如何设计。

（1）若想用一串序列去预测另一串序列，那么输入输出都是张量 (例如语音识别 或机器翻译 一个中文句子翻译成英文句子（一个单词算作一个向量），机器翻译还是个特例，因为两个序列的长短可能不同，要用到seq2seq；

（2）若想用一串序列去预测一个值，那么输入是张量，输出是矩阵 （例如，情感分析就是用一串单词组成的句子去预测说话人的心情）

Feedforward 能做的是向量对向量的one-to-one mapping，

Recurrent 将其扩展到了序列对序列 sequence-to-sequence mapping.

但单个向量也可以视为长度为1的序列。所以有下图几种类型：

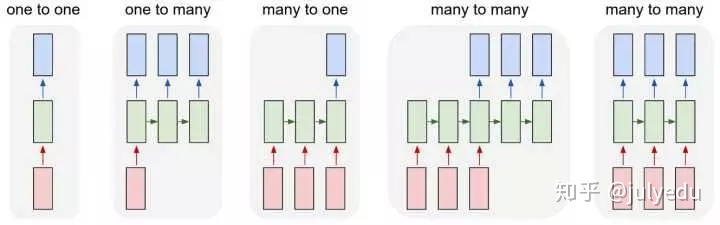
除了最左侧的one to one是feedforward 能做的，右侧都是Recurrent所扩展的

若还想知道更多

（1）可以将Recurrent的横向操作视为累积已发生的事情，并且LSTM的memory cell机制会选择记忆或者忘记所累积的信息来预测某个时刻的输出。

（2）以概率的视角理解的话：就是不断的conditioning on已发生的事情，以此不断缩小sample space

（3）RNN的思想是: current output不仅仅取决于current input，还取决于previous state；可以理解成current output是由current input和previous hidden state两个输入计算而出的。并且每次计算后都会有信息残留于previous hidden state中供下一次计算。

35.什么是RNN？

解析：
RNNs的目的使用来处理序列数据。在传统的神经网络模型中，是从输入层到隐含层再到输出层，层与层之间是全连接的，每层之间的节点是无连接的。但是这种普通的神经网络对于很多问题却无能无力。例如，你要预测句子的下一个单词是什么，一般需要用到前面的单词，因为一个句子中前后单词并不是独立的。

RNNs之所以称为循环神经网路，即一个序列当前的输出与前面的输出也有关。具体的表现形式为网络会对前面的信息进行记忆并应用于当前输出的计算中，即隐藏层之间的节点不再无连接而是有连接的，并且隐藏层的输入不仅包括输入层的输出还包括上一时刻隐藏层的输出。

理论上，RNNs能够对任何长度的序列数据进行处理。但是在实践中，为了降低复杂性往往假设当前的状态只与前面的几个状态相关，下图便是一个典型的RNNs：

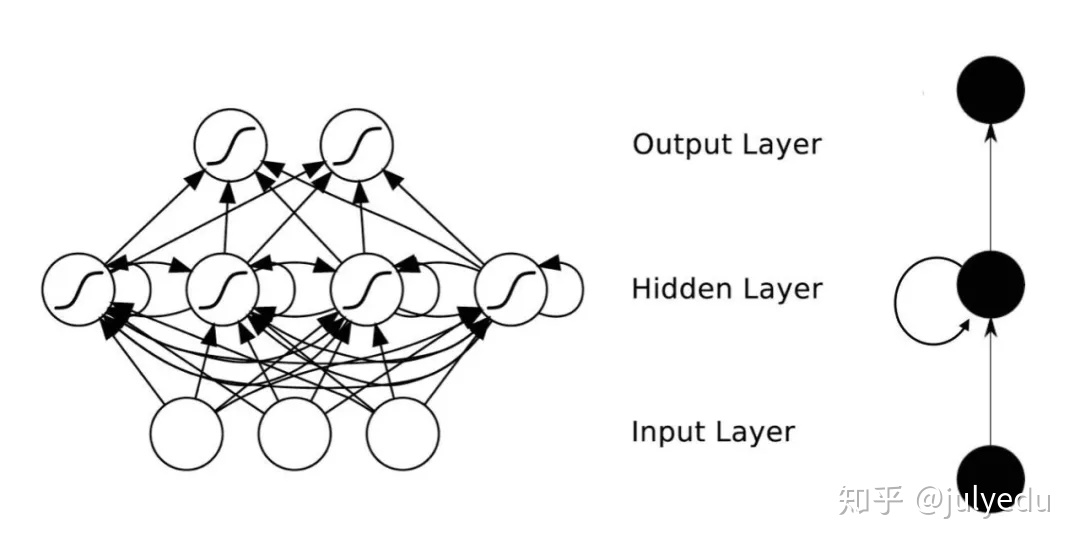
RNNs包含输入单元(Input units)，输入集标记为{x0,x1,…,xt,xt+1,…}，而输出单元(Output units)的输出集则被标记为{y0,y1,…,yt,yt+1.,…}。RNNs还包含隐藏单元(Hidden units)，我们将其输出集标记为{s0,s1,…,st,st+1,…}，这些隐藏单元完成了最为主要的工作。你会发现，在图中：有一条单向流动的信息流是从输入单元到达隐藏单元的，与此同时另一条单向流动的信息流从隐藏单元到达输出单元。在某些情况下，RNNs会打破后者的限制，引导信息从输出单元返回隐藏单元，这些被称为“Back Projections”，并且隐藏层的输入还包括上一隐藏层的状态，即隐藏层内的节点可以自连也可以互连。

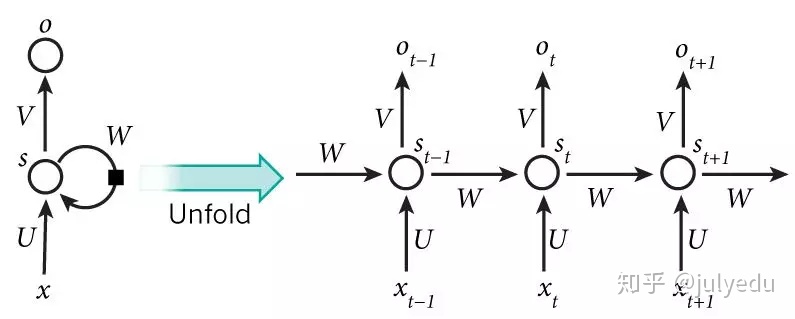
上图将循环神经网络进行展开成一个全神经网络。例如，对一个包含5个单词的语句，那么展开的网络便是一个五层的神经网络，每一层代表一个单词。对于该网络的计算过程如下：

（1）xt表示第t,t=1,2,3…步(step)的输入。比如，x1为第二个词的one-hot向量(根据上图，x0为第一个词)；

（2） st为隐藏层的第t步的状态，它是网络的记忆单元。 st根据当前输入层的输出与上一步隐藏层的状态进行计算。st=f(Uxt+Wst−1)，其中f一般是非线性的激活函数，如tanh或ReLU，在计算s0时，即第一个单词的隐藏层状态，需要用到s−1，但是其并不存在，在实现中一般置为0向量；

（3）ot是第t步的输出，如下个单词的向量表示，ot=softmax(Vst).

---

以下转自：https://zhuanlan.zhihu.com/p/39965633

36、简单说下sigmoid激活函数

解析：

常用的非线性激活函数有sigmoid、tanh、relu等等，前两者sigmoid/tanh比较常见于全连接层，后者relu常见于卷积层。这里先简要介绍下最基础的sigmoid函数（btw，在本博客中SVM那篇文章开头有提过）。

sigmoid的函数表达式如下

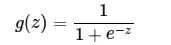
其中z是一个线性组合，比如z可以等于：b + w1x1 + w2x2。通过代入很大的正数或很小的负数到g(z)函数中可知，其结果趋近于0或1。

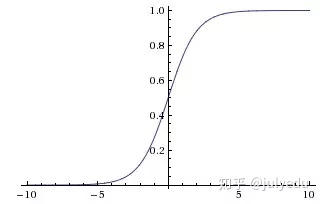
因此，sigmoid函数g(z)的图形表示如下（ 横轴表示定义域z，纵轴表示值域g(z) ）：

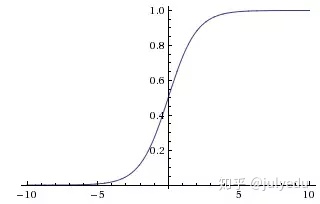
也就是说，sigmoid函数的功能是相当于把一个实数压缩至0到1之间。当z是非常大的正数时，g(z)会趋近于1，而z是非常小的负数时，则g(z)会趋近于0。

压缩至0到1有何用处呢？用处是这样一来便可以把激活函数看作一种“分类的概率”，比如激活函数的输出为0.9的话便可以解释为90%的概率为正样本。

举个例子，如下图（图引自Stanford机器学习公开课）

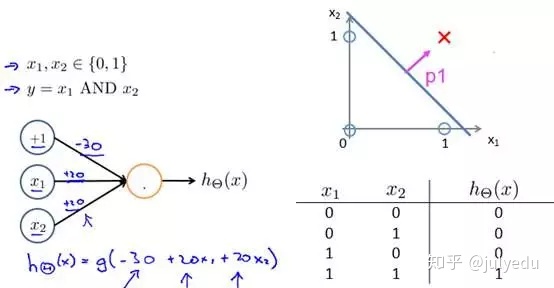
z = b + w1x1 + w2x2，其中b为偏置项 假定取-30，w1、w2都取为20

如果x1 = 0，x2 = 0，则z = -30，g(z) = 1/( 1 + e^-z )趋近于0。此外，从上图sigmoid函数的图形上也可以看出，当z=-30的时候，g(z)的值趋近于0

如果x1 = 0，x2 = 1，或x1 =1,x2 = 0，则z = b + w1x1 + w2x2 = -30 + 20 = -10，同样，g(z)的值趋近于0

如果x1 = 1，x2 = 1，则z = b + w1x1 + w2x2 = -30 + 201 + 201 = 10，此时，g(z)趋近于1。

换言之，只有x1和x2都取1的时候，g(z)→1，判定为正样本；而当只要x1或x2有一个取0的时候，g(z)→0，判定为负样本，如此达到分类的目的。

综上，sigmod函数，是逻辑斯蒂回归的压缩函数，它的性质是可以把分隔平面压缩到[0,1]区间一个数（向量），在线性分割平面值为0时候正好对应sigmod值为0.5，大于0对应sigmod值大于0.5、小于0对应sigmod值小于0.5；0.5可以作为分类的阀值；exp的形式最值求解时候比较方便，用相乘形式作为logistic损失函数，使得损失函数是凸函数；不足之处是sigmod函数在y趋于0或1时候有死区，控制不好在bp形式传递loss时候容易造成梯度弥撒。

37、rcnn、fast-rcnn和faster-rcnn三者的区别是什么

解析：
首先膜拜RBG（Ross B. Girshick）大神，不仅学术牛，工程也牛，代码健壮，文档详细，clone下来就能跑。断断续续接触detection几个月，将自己所知做个大致梳理，业余级新手，理解不对的地方还请指正。

传统的detection主流方法是DPM(Deformable parts models)， 在VOC2007上能到43%的mAP，虽然DPM和CNN看起来差别很大，但RBG大神说“Deformable Part Models are Convolutional Neural Networks”（http://arxiv.org/abs/1409.5403）。

CNN流行之后，Szegedy做过将detection问题作为回归问题的尝试（Deep Neural Networks for Object Detection），但是效果差强人意，在VOC2007上mAP只有30.5%。既然回归方法效果不好，而CNN在分类问题上效果很好，那么为什么不把detection问题转化为分类问题呢？

RBG的RCNN使用region proposal（具体用的是Selective Search Koen van de Sande: Segmentation as Selective Search for Object Recognition）来得到有可能得到是object的若干（大概10^3量级）图像局部区域，然后把这些区域分别输入到CNN中，得到区域的feature，再在feature上加上分类器，判断feature对应的区域是属于具体某类object还是背景。当然，RBG还用了区域对应的feature做了针对boundingbox的回归，用来修正预测的boundingbox的位置。

RCNN在VOC2007上的mAP是58%左右。RCNN存在着重复计算的问题（proposal的region有几千个，多数都是互相重叠，重叠部分会被多次重复提取feature），于是RBG借鉴Kaiming He的SPP-net的思路单枪匹马搞出了Fast-RCNN，跟RCNN最大区别就是Fast-RCNN将proposal的region映射到CNN的最后一层conv layer的feature map上，这样一张图片只需要提取一次feature，大大提高了速度，也由于流程的整合以及其他原因，在VOC2007上的mAP也提高到了68%。

探索是无止境的。Fast-RCNN的速度瓶颈在Region proposal上，于是RBG和Kaiming He一帮人将Region proposal也交给CNN来做，提出了Faster-RCNN。Fater-RCNN中的region proposal netwrok实质是一个Fast-RCNN，这个Fast-RCNN输入的region proposal的是固定的（把一张图片划分成n*n个区域，每个区域给出9个不同ratio和scale的proposal），输出的是对输入的固定proposal是属于背景还是前景的判断和对齐位置的修正（regression）。Region proposal network的输出再输入第二个Fast-RCNN做更精细的分类和Boundingbox的位置修正。

Fater-RCNN速度更快了，而且用VGG net作为feature extractor时在VOC2007上mAP能到73%。个人觉得制约RCNN框架内的方法精度提升的瓶颈是将dectection问题转化成了对图片局部区域的分类问题后，不能充分利用图片局部object在整个图片中的context信息。

可能RBG也意识到了这一点，所以他最新的一篇文章YOLO（http://arxiv.org/abs/1506.02640）又回到了regression的方法下，这个方法效果很好，在VOC2007上mAP能到63.4%，而且速度非常快，能达到对视频的实时处理（油管视频：https://www.youtube.com/channel/UC7ev3hNVkx4DzZ3LO19oebg），虽然不如Fast-RCNN，但是比传统的实时方法精度提升了太多，而且我觉得还有提升空间。

38、在神经网络中，有哪些办法防止过拟合？

解析：
缓解过拟合：
① Dropout
② 加L1/L2正则化
③ BatchNormalization
④ 网络bagging

39、CNN是什么，CNN关键的层有哪些？

解析：
CNN是卷积神经网络，具体详见此文：https://blog.csdn.net/v_july_v/article/details/51812459。

其关键层有：
① 输入层，对数据去均值，做data augmentation等工作
② 卷积层，局部关联抽取feature
③ 激活层，非线性变化
④ 池化层，下采样
⑤ 全连接层，增加模型非线性
⑥ 高速通道，快速连接
⑦ BN层，缓解梯度弥散

40、GRU是什么？GRU对LSTM做了哪些改动？

解析：
GRU是Gated Recurrent Units，是循环神经网络的一种。

GRU只有两个门（update和reset），LSTM有三个门（forget，input，output），GRU直接将hidden state 传给下一个单元，而LSTM用memory cell 把hidden state 包装起来。

---

以下转自：https://zhuanlan.zhihu.com/p/40051944

41、请简述应当从哪些方向上思考和解决深度学习中出现的的over fitting问题？

解析：
如果模型的训练效果不好，可先考察以下几个方面是否有可以优化的地方。

(1)选择合适的损失函数（choosing proper loss ）

神经网络的损失函数是非凸的，有多个局部最低点，目标是找到一个可用的最低点。非凸函数是凹凸不平的，但是不同的损失函数凹凸起伏的程度不同，例如下述的平方损失和交叉熵损失，后者起伏更大，且后者更容易找到一个可用的最低点，从而达到优化的目的。

• Square Error（平方损失）

• Cross Entropy（交叉熵损失）

(2)选择合适的Mini-batch size
采用合适的Mini-batch进行学习，使用Mini-batch的方法进行学习，一方面可以减少计算量，一方面有助于跳出局部最优点。因此要使用Mini-batch。更进一步，batch的选择非常重要，batch取太大会陷入局部最小值，batch取太小会抖动厉害，因此要选择一个合适的batch size。

(3)选择合适的激活函数（New activation function）

使用激活函数把卷积层输出结果做非线性映射，但是要选择合适的激活函数。

• Sigmoid函数是一个平滑函数，且具有连续性和可微性，它的最大优点就是非线性。但该函数的两端很缓，会带来猪队友的问题，易发生学不动的情况，产生梯度弥散。

• ReLU函数是如今设计神经网络时使用最广泛的激活函数，该函数为非线性映射，且简单，可缓解梯度弥散。

(4)选择合适的自适应学习率（apdative learning rate）

• 学习率过大，会抖动厉害，导致没有优化提升

• 学习率太小，下降太慢，训练会很慢

(5)使用动量（Momentum）

在梯度的基础上使用动量，有助于冲出局部最低点。

如果以上五部分都选对了，效果还不好，那就是产生过拟合了，可使如下方法来防止过拟合，分别是

• 1.早停法（earyly stoping）。早停法将数据分成训练集和验证集，训练集用来计算梯度、更新权重和阈值，验证集用来估计误差，若训练集误差降低但验证集误差升高，则停止训练，同时返回具有最小验证集误差的连接权和阈值。

• 2.权重衰减（Weight Decay）。到训练的后期，通过衰减因子使权重的梯度下降地越来越缓。

• 3.Dropout。Dropout是正则化的一种处理，以一定的概率关闭神经元的通路，阻止信息的传递。由于每次关闭的神经元不同，从而得到不同的网路模型，最终对这些模型进行融合。

• 4.调整网络结构（Network Structure）。

限时1元秒杀>>深度学习特训 第八期[深度学习集训营 预习课之一] - 七月在线

42、神经网络中，是否隐藏层如果具有足够数量的单位，它就可以近似任何连续函数？

解析：
通用逼近性定理指出，一个具有单个隐藏层和标准激活函数的简单前馈神经网络（即多层感知器），如果隐藏层具有足够数量的单位，它就可以近似任何连续函数。让我们在实践中看一下，看看需要多少单位来近似一些特定函数。

方法：我们将在 50 个数据点 (x,y) 上训练一个 1 层神经网络，这些数据点从域 [-1,1] 上的以下函数中绘制，所得拟合的均方误差（mean square error，MSE）。我们将尝试以下函数（你可随时通过更改以下代码来尝试自己的函数。）

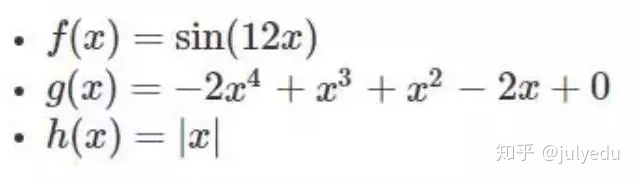
假设： 随着隐藏层中单位的数量增加，所得拟合的正确率（Accuracy）将会增加（误差将会减少）。

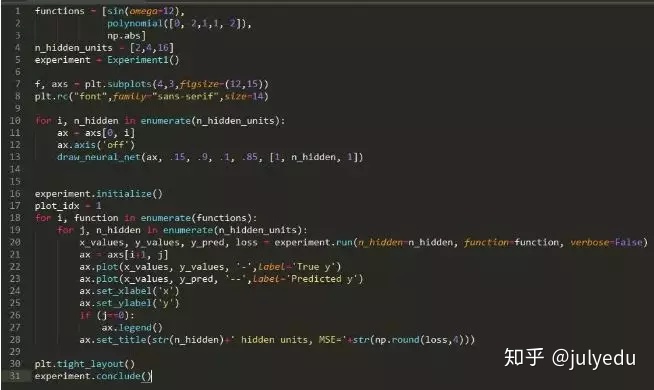
运行实验所需的时间： 91.595 s

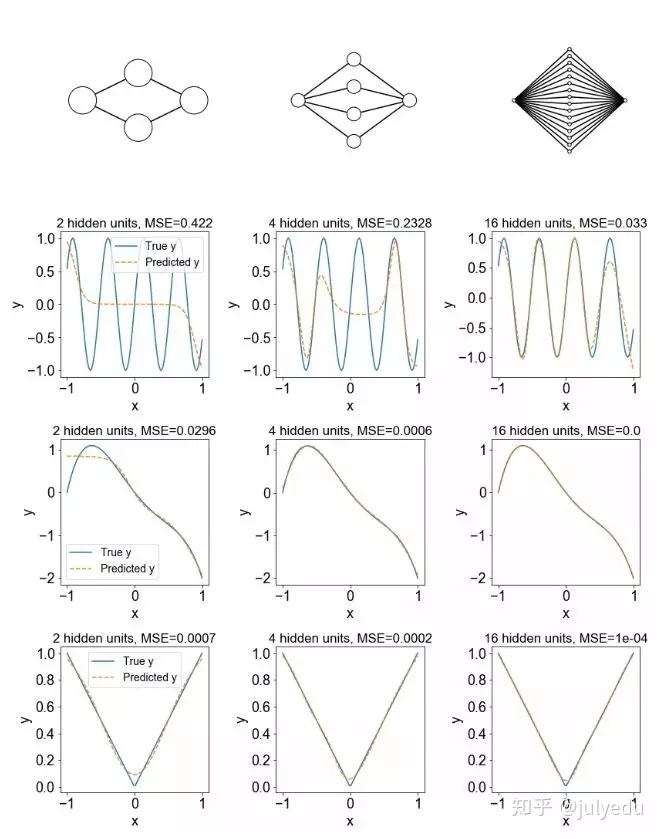
结论： 随着隐藏单位数量的增加，训练数据的逼近误差一般会减小。

讨论： 尽管通用逼近定理指出，具有足够参数的神经网络可以近似一个真实的分类 / 回归函数，但它并没有说明这些参数是否可以通过随机梯度下降这样的过程来习得。另外，你可能想知道我们是否可以从理论上计算出需要多少神经元才能很好地近似给定的函数。你可参阅论文《NEURAL NETWORKS FOR OPTIMAL APPROXIMATION OFSMOOTH AND ANALYTIC FUNCTIONS》对此的一些讨论。

43、为什么更深的网络更好？

解析：
在实践中，更深的多层感知器（具有超过一个隐藏层）在许多感兴趣的任务上的表现，在很大程度上都胜过浅层感知器。为什么会出现这种情况呢？有人认为，更深的神经网络仅需更少的参数就可以表达许多重要的函数类。

理论上已经表明，表达简单的径向函数和组合函数需要使用浅层网络的指数级大量参数。但深度神经网络则不然。

剧透警告：我打算用实验来验证这些论文，但我不能这样做（这并不会使论文的结果无效——仅仅因为存在一组神经网络参数，并不意味着它们可以通过随机梯度下降来轻松习得）。

我唯一能做的就是，某种程度上可靠地再现来自论文《Representation Benefits of Deep Feedforward Networks》的唯一结果，这篇论文提出了一系列困难的分类问题，这些问题对更深层的神经网络而言更容易。

方法： 该数据集由沿着 x 轴的 16 个等距点组成，每对相邻点都属于相反的类。一种特殊类型的深度神经网络（一种跨层共享权重的神经网络）具有固定数量（152）的参数，但测试了层的不同数量。

假设： 随着具有固定数量参数的神经网络中层数的增加，困难的分类问题的正确率将得到提高。

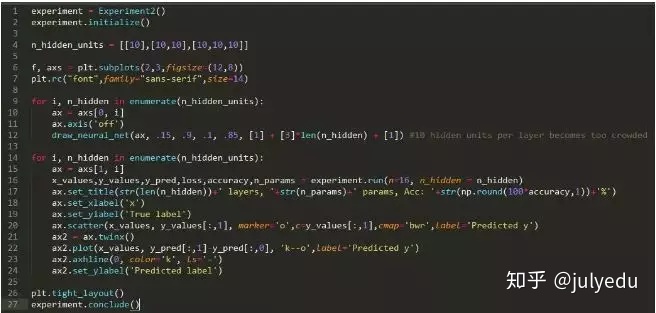
运行实验所需的时间： 28.688 s

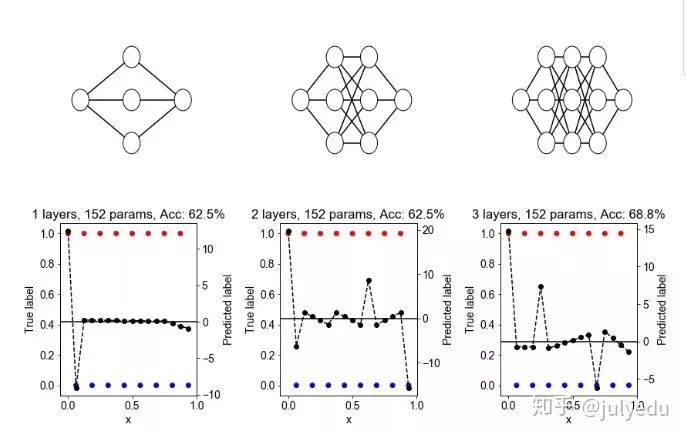
此处，红点和蓝点代表属于不同类别的点。黑色的虚线表示最接近神经网络学习的训练数据近似值（若神经网络分配的分数大于零，则被预测为红点；否则，被预测为蓝点）。零线显示为黑色。

结论： 在大多实验中，正确率随深度的增加而增加。

讨论： 似乎更深的层允许从输入到输出的学习到的函数出现更多“急弯”。这似乎跟神经网络的轨迹长度有关（即衡量输入沿着固定长度的一维路径变化时，神经网络的输出量是多少）。轨迹长度论文：https://arxiv.org/pdf/1606.05336.pdf

44、更多的数据是否有利于更深的神经网络？

解析：
深度学习和大数据密切相关；通常认为，当数据集的规模大到足够克服过拟合时，深度学习只会比其他技术（如浅层神经网络和随机森林）更有效，并更有利于增强深层网络的表达性。我们在一个非常简单的数据集上进行研究，这个数据集由高斯样本混合而成。

方法： 数据集由两个 12 维的高斯混合而成，每个高斯生成属于一个类的数据。两个高斯具有相同的协方差矩阵，但也意味着在第 i 个维度上有 1/i1/i 单位。这个想法是基于：有一些维度，允许模型很容易区分不同的类，而其他维度则更为困难，但对区别能力还是有用的。

假设： 随着数据集大小的增加，所有技术方法的测试正确率都会提高，但深度模型的正确率会比非深度模型的正确率要高。我们进一步预计非深度学习技术的正确率将更快地饱和。

运行实验所需的时间： 138.239 s

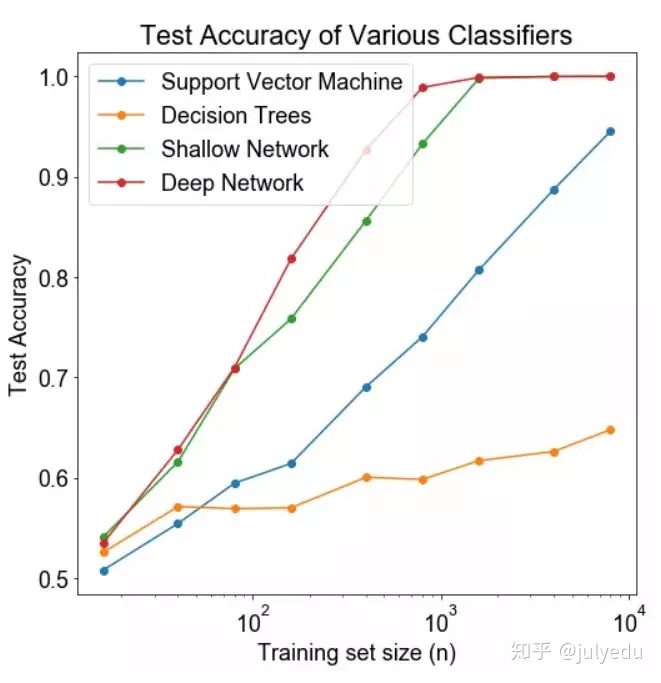
结论： 神经网络在数据集大小方面上表现始终优于 SVM 和随机森林。随着数据集大小的增加，性能上的差距也随之增加，至少在神经网络的正确率开始饱和之前，这表明神经网络更有效地利用了不断增加的数据集。然而，如果有足够的数据，即使是 SVM 也会有可观的正确率。深度网络比浅层网络的表现更好。

讨论： 虽然增加的数据集大小确实会像我们预计的那样有利于神经网络。但有趣的是，在相对较小的数据集上，神经网络已经比其他技术表现得更好。似乎 2 层网络并没有显著的过拟合，即使我们预计某些特征（如 6-12 特征，信号水平低）导致网络过拟合。同样有趣的是，SVM 看上去似乎有足够的数据来接近于 1.0。

45、不平衡数据是否会摧毁神经网络？

解析：
当数据集不平衡时（如一个类的样本比另一个类还多），那么神经网络可能就无法学会如何区分这些类。在这个实验中，我们探讨这一情况是否存在。同时我们还探讨了过采样是否可以减轻问题带来的影响，这是一种流行的补救措施，该措施使用少数类中抽样替换的样本。

方法：我们生成两个二维的结果（结果未在这里显示，表明相同的结果适用于更高维）高斯，每个产生属于一个类别的数据。两个高斯具有相同的协方差矩阵，但它们的意思是在第 i 个维度上相距 1/i1/i 单位。每个训练数据集由 1,200 个数据点组成，但我们将类别不平衡从 1:1 变为 1:99。测试数据集以 1:1 的比例保持固定，以便于性能比较，并由 300 个点组成。我们还会在每种情况下显示决策边界。

假设：我们预计测试正确率会随着类别不平衡的增加而降低，但我们预计过采样可以缓解这个问题。

运行实验所需的时间： 392.157 s


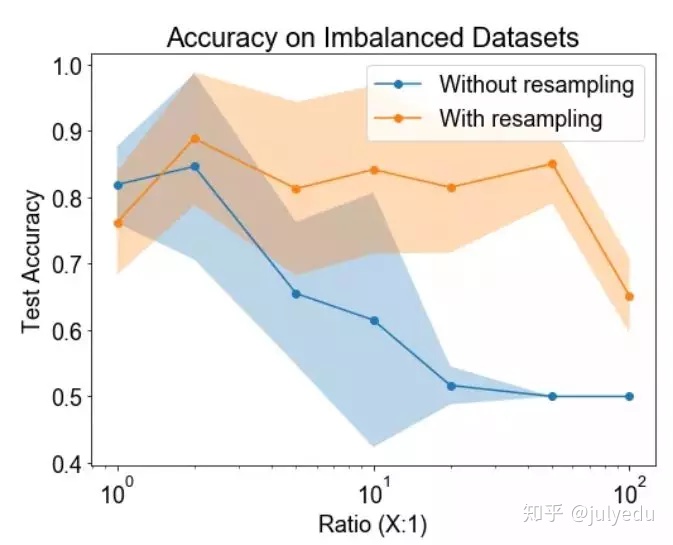
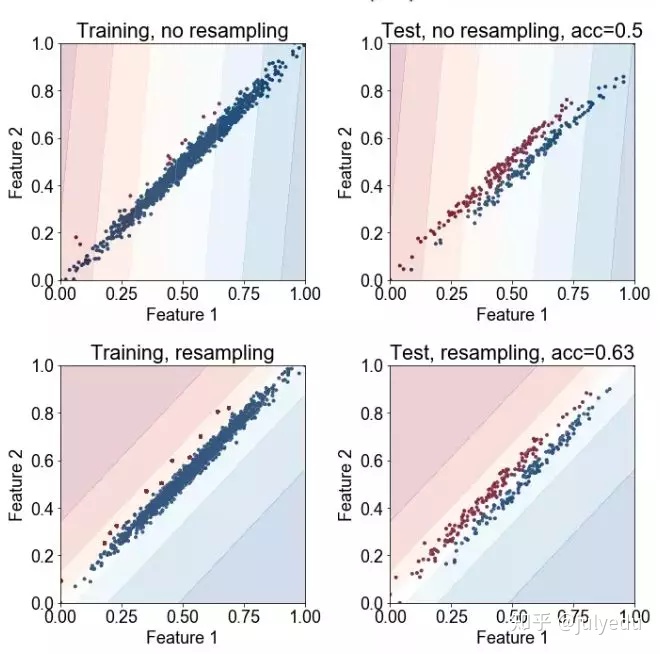
最下面的四张图显示了连同训练点（左）或测试点（右）绘制的决策边界的数量。第一行显示没有重采样法的结果，底部显示了使用重采样法的结果。

结论： 研究结果表明，类的不平衡无疑地降低了分类的正确率。重采样法可以显著提高性能。

讨论： 重采样法对提高分类正确率有显著的影响，这可能有点让人惊讶了，因为它并没有将分类器展示少数类中的新训练的样本。但该图显示，重采样法足以“助推（nudge）”或将决策边界推向正确的方向。在重采样法不是有效的情况下，那么可能需要复合方式来合成新的训练样本，以提高正确率。

---

以下转自：https://zhuanlan.zhihu.com/p/40135356

46、你如何判断一个神经网络是记忆还是泛化?

解析：以上是关于2_深度学习知识点的主要内容，如果未能解决你的问题，请参考以下文章

kpu 处理器_深度学习及 KPU 基础知识

1_深度学习知识点

深度学习笔记总结（待更新）

3_深度学习知识点

深度学习 线代知识

如何深度学习技术专业相关知识点的思维认知探讨